Note:
- Dataset and ipython notebook of this post is available at SPISim’s github page: [HERE]
- This notebook may be better rendered by nbviewer and can be viewed [HERE].


[This blog post is written in preparation for the presentation of the same title to be given at the 2019 DesignCon IBIS Summit. Presentation slides and audio recording are linked at the bottom of this post.]
This paper is written by both Wei-hsing Huang (principle consultant at SPISim USA) and Wei-kai Shih, who is Tokyo based.
Here in US, one of IBIS committee’s working groups, IBIS-ATM (advanced technology modeling) has regular meeting on Tue. I try to call-in whenever possible to gain insights on upcoming modeling trends. During mid 2018, DDR5 related topics were brought up: Existing AMI reference flow described in the spec. focuses on differential or SERDES. For example, the stimulus waveform is from -0.5 to 0.5 and/or a single impulse response is used for analysis, thus assuming symmetric rise time (Rt) and fall time (Ft) mostly. Whether this reference flow can be applied to DDR, which may have asymmetric Rt/Ft and single-ended like DQ, is the center of discussion. Different EDA companies in this work group have different opinions. Some think the flow can be used directly with minimal change while others think the flow has fundamental shortcomings for DDR. Thing about IBIS spec. change is that whoever think the current version has deficiencies needs to write a “buffer issue resolution document (BIRD)”. Doing so will inevitably disclose some of the trade secrets or expose shortcoming of the the tool. As a result, while there are companies which think change may be needed, no flow change have been proposed at this point. As a model maker, I wonder then how existing flow can be applied to DDR without major change? Thus this study is to demonstrate “one” possible implementation. Existing EDA companies may have more sophisticated algorithms/implementations to support this asymmetric condition, but the existence of “one” such possible flow may convince model makers that it’s time to think about how DDR AMI may be implemented rather than waiting for the unlikely spec. change.
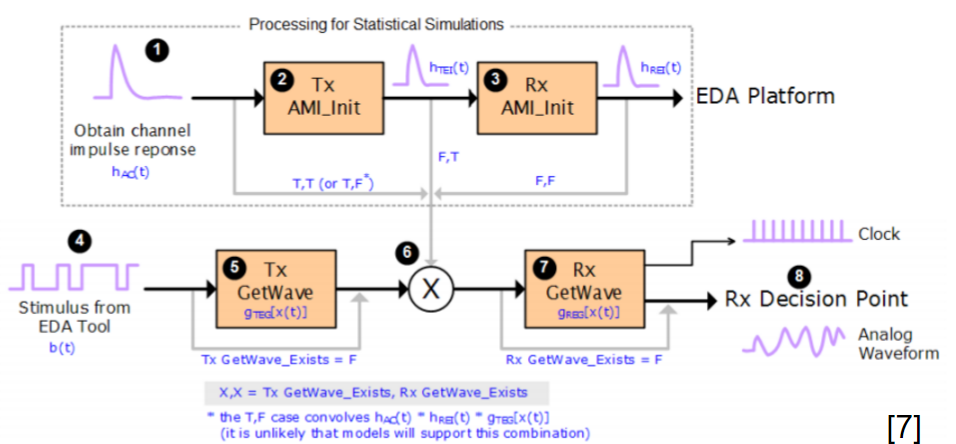
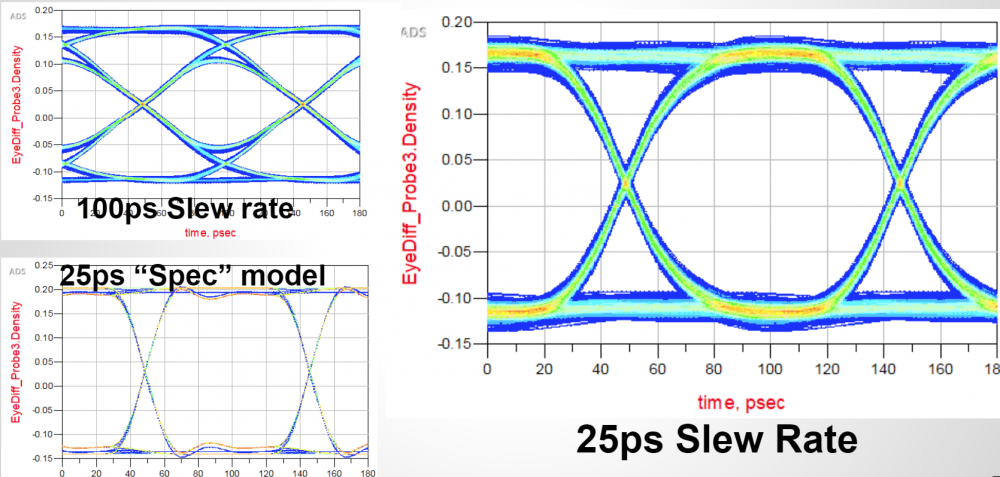
There are both “statistical” and “bit-by-bit” flows in channel analysis. In either case, the first step an EDA tool will do before calling AMI model is “channel calibration”. According to the spec. the impulse response of the channel, which includes analog buffer, is obtained here. For a SERDES design which has no asymmetric Rt/Ft issue, this impulse is then sent to TX AMI followed by RX AMI, resulting impulse response is then calculated using probability density function (PDF), integrated to be cumulative density function (CDF), then obtain bathtub plots etc.

The textbook definition of an impulse response is from a “delta response” input which happens at the infinite small time step. In real situation, there is no such thing as an “infinite small time step”. The minimal step used by a simulator is a “time step” which is usually 1ps or more. Buffer will not toggle from low to high back to low in a single time step. So in reality, simulator often uses step response then take derivative to get impulse response. Now the problem comes: for an analog channel with asymmetric Rt/Ft, these two step response (ignoring the sign) are different. That means we will have two different impulse response, then which one should be send to AMI models? A note here up front is that it’s EDA tool which sets up the calibration, so it has any nodal information, such as pad of Tx and Rx analog buffer, if needed.
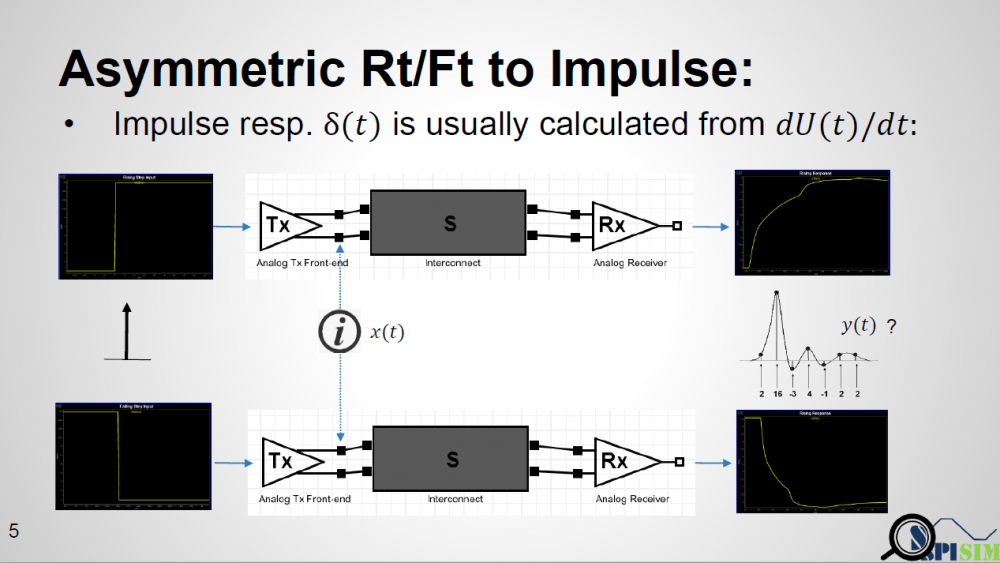
One may think that there is no such limitation that an AMI model can only be called once. So theoretically, a simulator can run analysis flow twice… impulse calculated from rising step response is used for the first time and the one from falling step response is used for the second time. However, not only is this not efficient, a model may not be implemented properly such that calling AMI_Init again right after AMI_Close may cause crash if it’s in the same process and model pointer was not released completely. Thus doing so may hamper a simulator’s robustness.
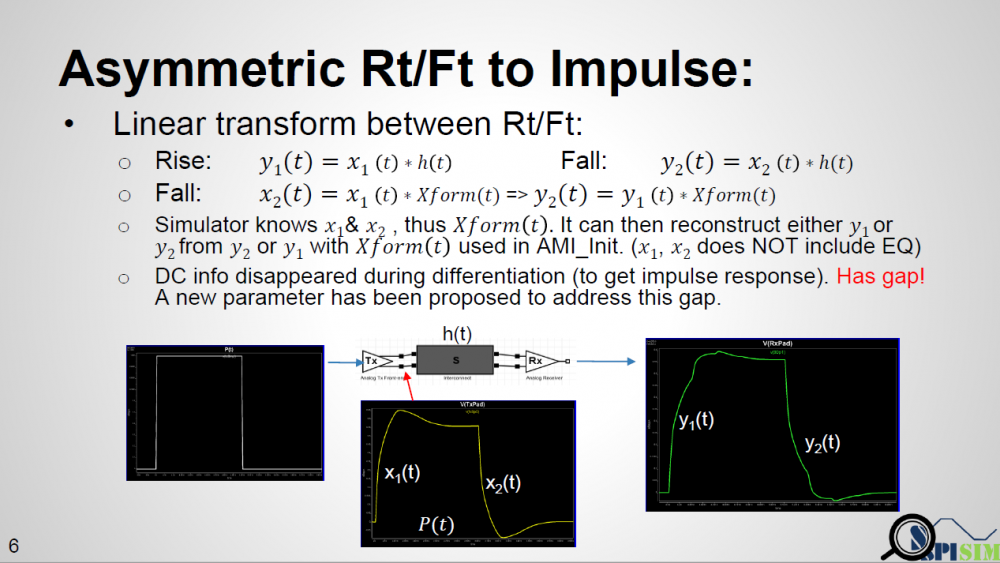
As depicted in the picture above… if a simulator uses a long UI pulse to calibrate the channel, then both rising and falling step response are included in one simulation. Now let the data captured at Tx analog pad as X1 and X2 for rising and falling portion respectively, the data captured at Rx analog pad Y1 and Y2 will be X1 and X2 convolved with interconnect’s transfer function, which is LTI. If we derive a Xform(t) which is transfer function between X1 and X2, then that Xform(t) should also be able to transform between Y1 and Y2. That means if a simulator can calculate Xform(t) it self, then regardless the impulse response it sent to AMI models is calculated from rising or falling step response, it can always “reconstruct” the result from the other type of impulse response using this Xform(t) function.
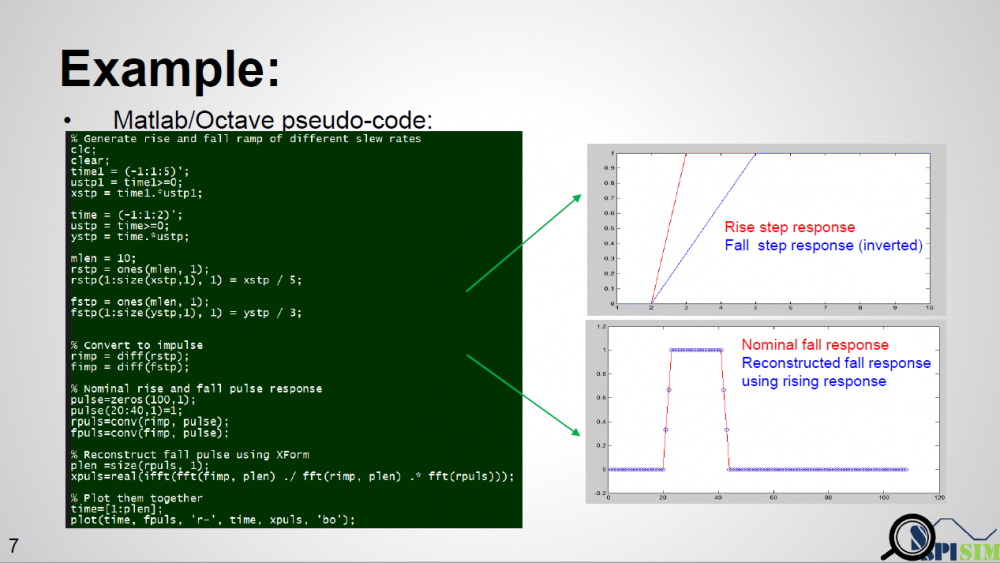
To prove this concept, we have written a simple matlab script taking step inputs of different slew rate, say inp1 and inp2. It calculates the Xform(t) function from both inputs and then reconstruct the response out2′ from out1. When overlaying nominal output out2 and reconstructed out2′ together, we can see that they match very well, thus prove the concept.

Once we have response from both different slew rates, we can construct their respective eyes then use each one’s different portion to construct a synthesized eye. Such eye will not be symmetric like that calculated from SERDES.
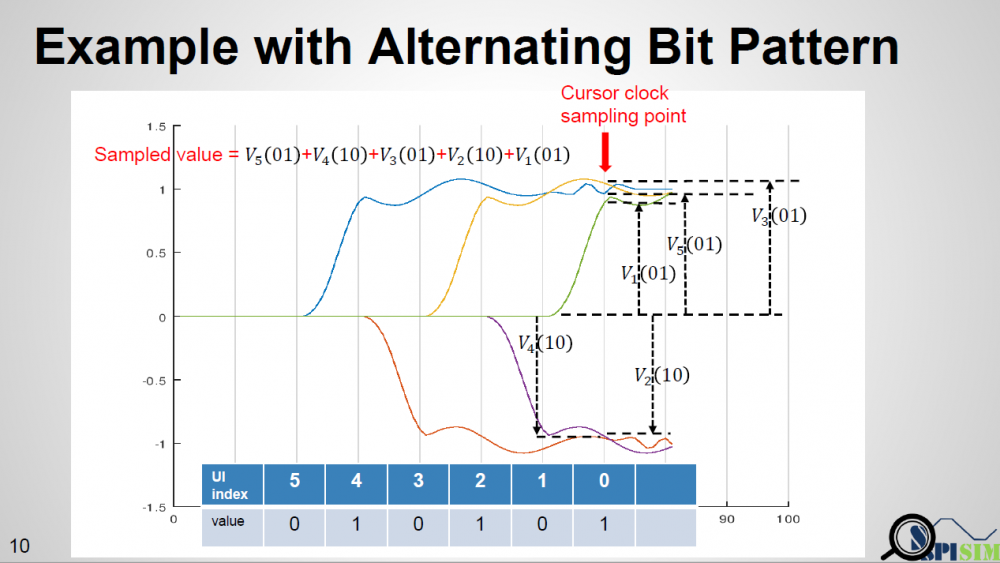
When calculating PDF for asymmetric case, one may also need to consider the precedent bit’s value and use a tree like structure to keep track of possible bit sequence. For example, for a typical SERDES bit sequence, if encoding is not considered, each bit will have 50% one and 50% zero. PDF is constructed based on that assumption. But in an asymmetric case, if the data used at the cursor is from rising response, then the cursor bit must be 1 while (cursor – 1) must be zero. If (cursor – 2) is 1 again, then the tail of falling response at (cursor – 1) will be superimposed to the cursor data. That is, we can’t treat each bit to have same 50% probability when constructing PDF. It’s not a binomial distribution as each occurrence is not independent. A simulator may need to determine the maximum bit length to keep track of first, then based on that depth to form tree-like sequence which leads to the rising or falling steps at the cursor location. Finally use superimpose to construct the overall response.

According to the reference flow for the bit-by-bit case: equalized Tx output from digital bit sequence is converted with channel’s impulse response. The resulting waveform is then sent to Rx EQ before getting final results. Either Tx EQ or Rx EQ or both may not be LTI so usage of aforementioned Xform(t) is not applicable.
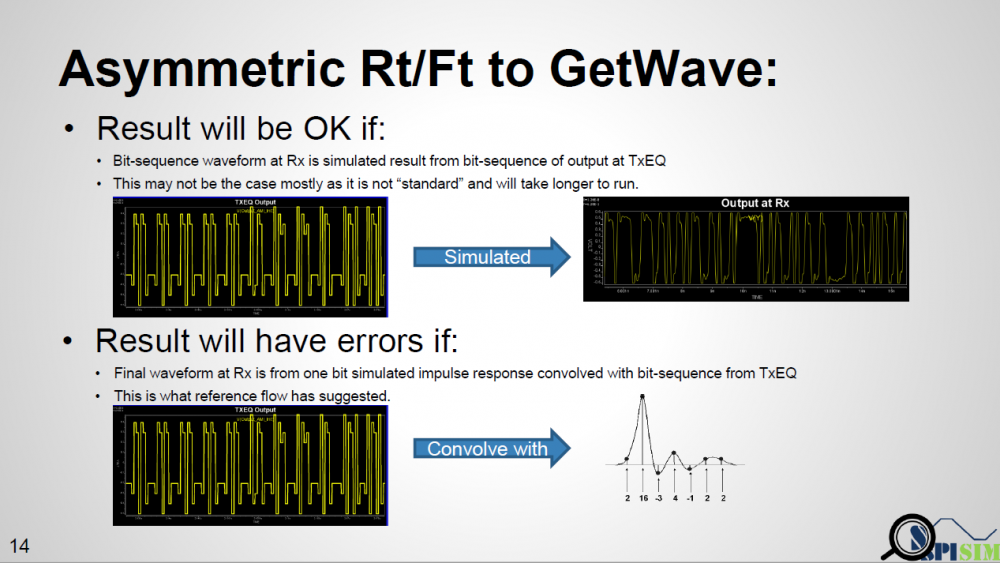
As a fruit of thought… the spec. only mentions that in a bit-by-bit mode, the output of Tx AMI model is equalized digital sequence, while input to the Rx EQ must be the channel response from that sequence, then are there other ways to get such response to Rx yet with different Rt/Ft considered?
One example is like shown in top half of the picture above. If a simulator takes that equalized digital input and “simulate” to get final response, then this “simulation process” should have taken different Rt/Ft into account and has valid results. However, this process will be slow and I don’t think any simulator is doing it this way. Furthermore, the spec. specifically say it needs to “convolve” with impulse response. First of all, this impulse can be from rising or falling. Secondly, even we decide to decovolve with input first (thus has sequences of different delta response) then convolve with pulse response (i.e. one simulated UI), will there be any issue?

From the plot above… we can see that when a pulse has different rising and falling slew rate, using superimpose to construct 011… will find “glitches” at the trailing high state portion. The severity of this “glitches” depends on how much difference the Rt/Ft is. So using a pulse response here will still not work.
A simple matlab script has also been written to demonstrate occurrence of such “glitches”. This proves that not only using an impulse response to convolve with Tx EQ’s output is problematic, even using a full simulated pulse (which has asymmetric Rt/Ft’s effect) to convolve delta sequences (this delta sequence is original TX EQ’s output deconvolve with one digital bit) will still be problematic. Glitches will happen for consecutive ones or zeros due to the mismatches of Rt and Ft. Thus one must use rise step and fall step response instead when doing such kind of convolution.
In this presentation, we discussed how existing AMI flow may be applied to asymmetric Rt/Ft such as those often seen in DDR case. A “smarter” EDA tool should be able to handle this situation without changing on spec.’s reference flow. When a channel analysis is performed in a “statistical” flow, an EDA tool can obtain waveform data at both Tx and Rx analog buffer’s pads during calibration process. Such data can be used to construct a transform function, XForm(t). With this function, impulse response through EQ can be reconstructed and thus built an asymmetric eye. Tree structure may be needed to keep track of possible bit combinations. In a “bit-by-bit” flow, the current spec. may be too specific as it forces to use convolution of TX EQ’s output with channel’s impulse response before sending to RX EQ. Such direct convolution may be problematic. A “smarter” simulator may calculate it using different method without changing data output from TX EQ and input to the RX EQ. Step response should be used as different Rt/Ft will cause “glitches” when consecutive ones/zeros are present if convolution method is used.
Presentation: [HERE] (http://www.spisim.com/support/paperetc/20180202_DesignConSummit_SPISim.pdf)
Audio recording (English): [HERE]
In previous post, I mentioned about the “IBIS cook-book” as a good reference for the analog portion of the buffer modeling. Unfortunately, when it comes to the equalization part, i.e. AMI, there is no similar counterpart AFAIK. For the AMI modeling, the EQ algorithms need to be realized with algorithms/procedures implemented as spec. compliant APIs and written in C language. These functions then need to be compiled as a dynamic library in either dynamic link libraries (.dll on windows) or “shared objects (.so on linux-like). Different compiler and build tool has different ways to create such files. So it’s fair to say that many of these aspects are actually in the computer science/programming domains which are outside the electrical or modeling scopes. It is unlikely to have a document to detail all these processes step-by-step.
In this post, instead of writing those “programming” details, I would like to give a high-level overview about what different steps of the AMI modeling process are… from end to end. Briefly, they can be arranged in the following steps based on execution order:
The following sections will describe each part in details.
Analog modeling:
Believe it or not, the first step of AMI modeling is to create proper IBIS models… i.e. its analog portion. This is particular true if circuit being modeled belongs to TX. A TX AMI model is equalizing signals which includes its own analog buffer’s effect measured at the TX pad. So if there is no channel (pass-through) and it’s under nominal loading condition, the analog response of the TX will be the signals to be equalized. That is to say, without knowing what will be equalized (i.e. what the model’s analog behavior is), one can’t calculate the TX AMI model’s EQ parameters.

Take the plot above as an example. This is a FFE EQ circuit. The flat lines indicated by two yellow arrows are different de-emphasis settings, thus controlled by AMI. However, the rising/falling slew rate, wave shape and dc levels etc as circled in red are all analog behaviors. Thus an accurate IBIS model must be created first to establish the base lines for equalization. Recently, BIRD 194 has been proposed to use touch-stone file in lieu of an IBIS model… still the analog model must be there.
For a RX circuit, it may be easier as an input buffer is usually just a ESD clamp or terminator. Thus it doesn’t take much effort to create the IBIS model. Interested people may see my previous posts regarding various IBIS modeling topics.
Prepare collateral:
AMI’s data can be obtained from different sources: circuit simulation, lab/silicon measurement or data sheet. For simulation case, simulation must be done and the resulting waveform’s performance needs to be extracted. These values will serve as a “design targets” based on whitch AMI model’s parameters are being tuned.
For example, this is a typical TX waveform and measured data:
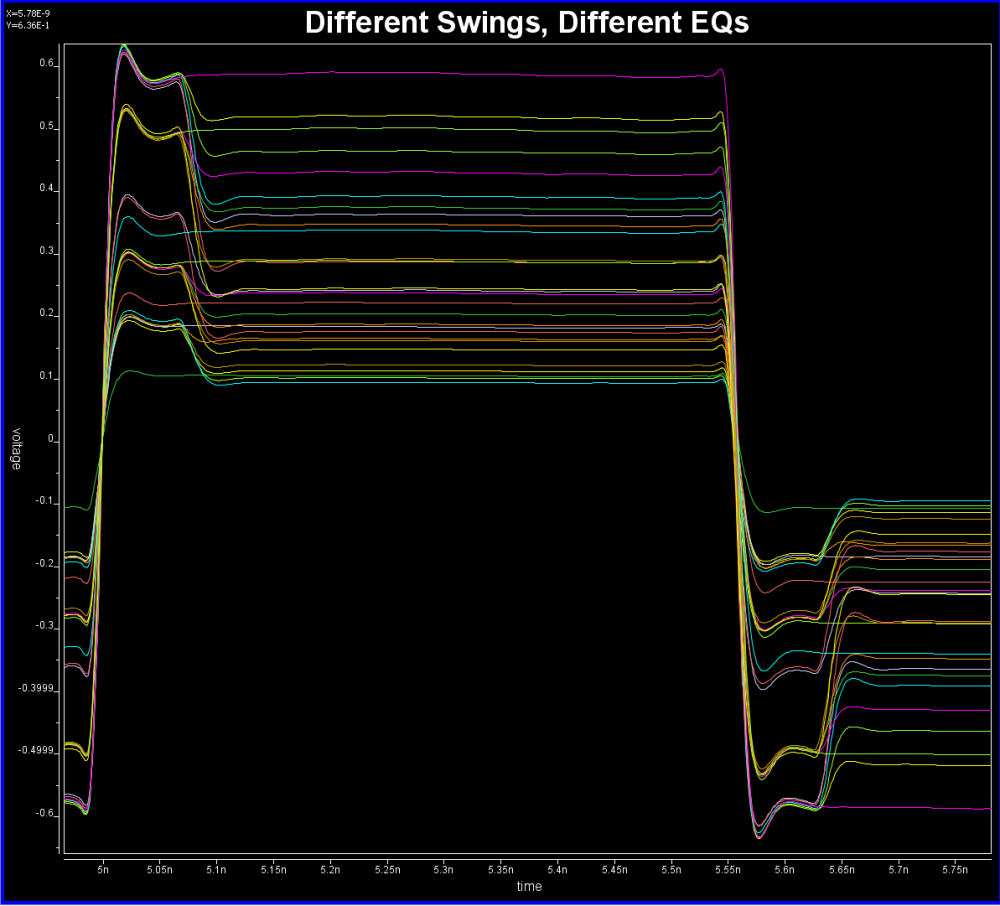
Various curves have been “lined-up” for easy post-processing. Using our VPro, we batch measured the value at the 5.3ns for different curves and created a table: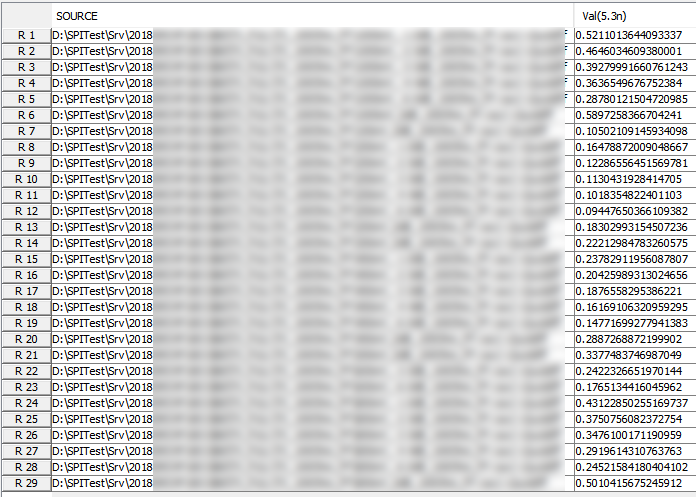 Similarly, data collected from measurement needs to be quantified. This may be done manually and maybe labor intensive as the noise is usually there:
Similarly, data collected from measurement needs to be quantified. This may be done manually and maybe labor intensive as the noise is usually there: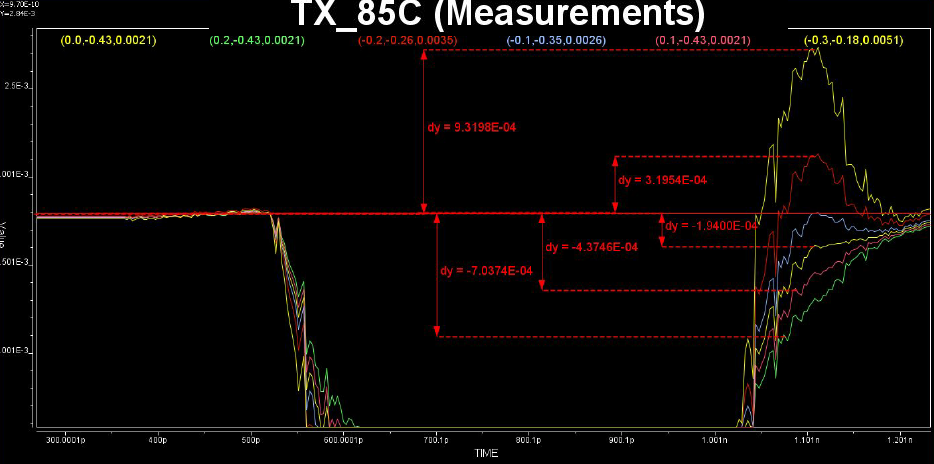
Some of the circuits may have response is in frequency domain. In this case, various points (DC, fundamental freq. 2X fundamental etc) needs to be measured like above.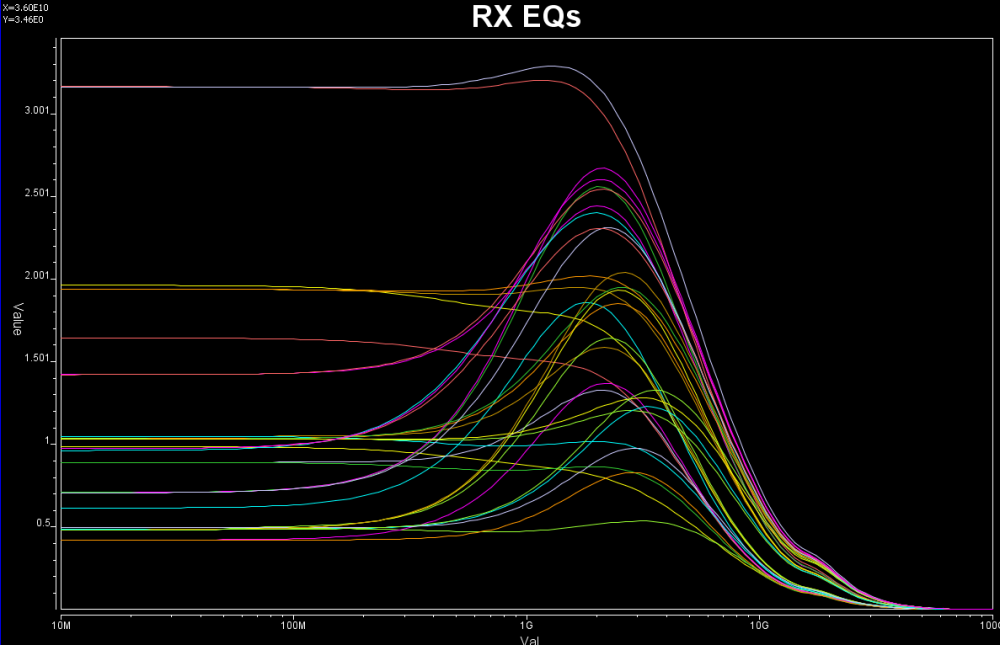
If it’s from data sheet, then the values are already there yet there may be different ways to realize such performance. For example, equations of different zeros and poles locations may all have same DC gain or gain at particular frequencies, so which one to pick may depending on other factors.
Define architecture:
Based on the collateral and the data sheet, the modeler needs to determine how the AMI models will be built. Usually it should reflect the IC’s design functions so there are not much ambiguity here. For example, if the Rx circuit has DFE/CDR functions, then the AMI models must also contain such modules. On the other hand, some data my be represented in different ways and proper judgement needs to be made. Take this waveform as an example: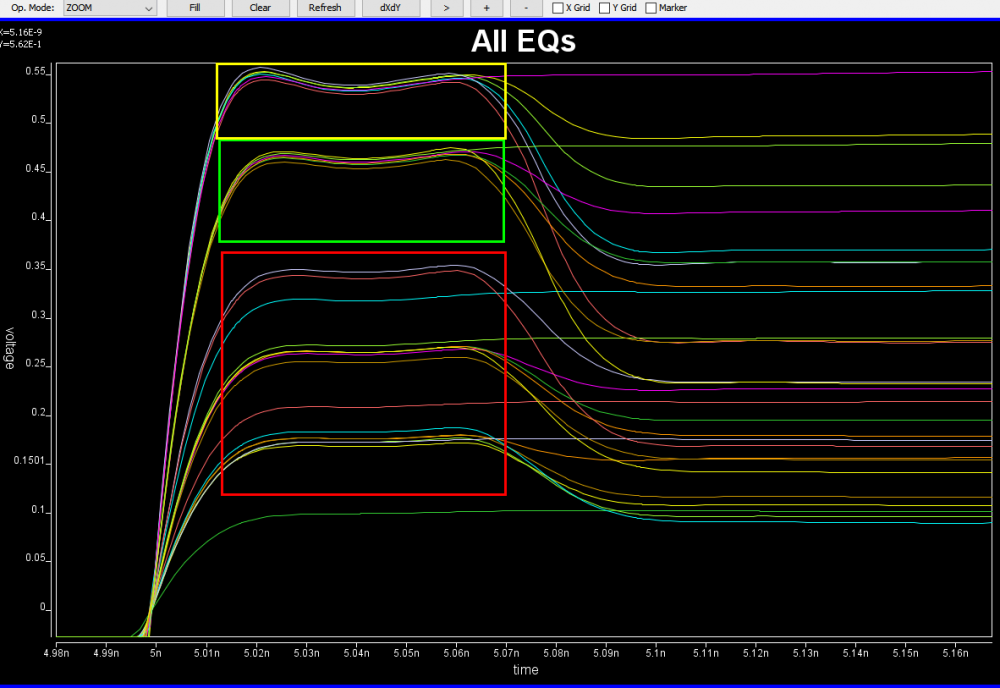
It’s already very obvious that it has a FFE with one post-tap. However, since the analog behavior needs to be represented by an IBIS model, then one needs to decide how these different behaviors, boxed in different colors, should be modeled. They can be constructed with several different IBIS models or a single IBIS model yet with some “scaling” block included so that IBIS of similar wave shapes can be squeezed or stretched. For a repeater, oftentimes people only care about what goes into and what comes out of this AMI model. The abilities to “probe” signals between a repeater’s RX and TX may be limited by the capabilities of simulator used. As a result, a modeler may have freedom determining which functions go into Rx and which go to Tx. In some cases, same model yet with different architecture needs to be created to meet different usage scenarios. An example has been discussed in our previous post [HERE]
Create models:
Once architecture is defined, next step is the actual C/C++ implementation. This is where programming part starts. Ideally, building blocks from previous projects are there already or will be created as a module so that they can be reused in the future. Multiple instance of the same models may be loaded together in some cases so the usage of “static” variables or function need to be very careful. Good programming practice comes into play here. I have seen models only work with certain bit-rate and 32 samples per UI. That indicates the model is “hard-coded”… it does not have codes to up-sample or down-sample the data based on the sampling-interval passed in from the API function. Accompanied with writing model’s C codes are unit testing, source revision control, compilations and dependencies check etc. The last one is particular important on linux as if your model relies on some external libraries and it is not linked statically, the same model running fine on developer’s machine will not even pass golden checker at user’s end…. because the library is not available there. Typically one will need to prepare several machines, virtual or not, which are “fresh” from OS installation and are the oldest “distros” one is willing to support. All these are typical software development process being applied toward this AMI modeling scope.
After the binary .dll/.so files are generated, then next step is to assemble a proper .ami files. Depending on parameter types (integer, values, corners etc), different flavors of syntax are available to create such file. In addition, different EDA simulators has different ways to present the parameter selections to its end user. So one may need to choose best syntax so that choices of parameter values will always be selected properly in targeted simulators. For example, if one already select TYP/MIN/MAX corner for the IBIS model, he/she should not have to do so again for the AMI part. It doesn’t make sense at all if a MIN AMI model will be used with MAX corner IBIS model… the corner should be “synchronized”.
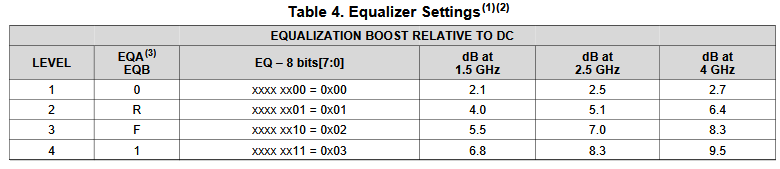
Once the model is ready, next step is to tune the parameters so that each of the performance target will be matched. Some interface, such as PCIe, has pre-defined FFE tap weights so there are no ambiguities. In most cases, one need to find the parameter’s values to match measured or simulated performance. Such tasks is very tedious and error prone if doing manually and process like our “AutoTune” will come very handy:
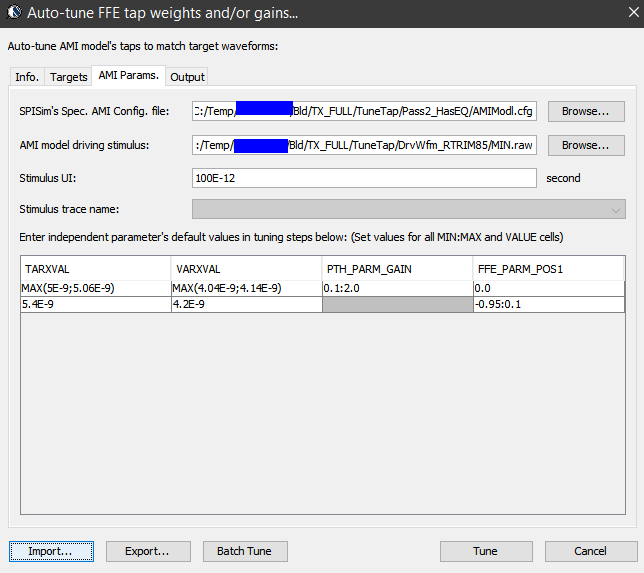
Basically, our tool let user specify matching target and tool will use bisection algorithm to find the tap values. Hundred of cases can be “tuned” in a matter of minutes. In some other cases, grid search may be needed.
Model validation:
Just like traditional IBIS, the first step of model validation is to run it through golden checker. However, one needs to do so on different platforms:

The golden checker didn’t start checking the included AMI binary models until quite recently. Basically it loads the .ibs file, identifies models with AMI functions, then check the .ami file syntax. Finally, the checker will load the associated .dll/.so files. Due to the fact that different OS platform loads binary files differently, that means certain models (e.g. .dll) can only be checked on associated platform (e.g. Windows). That’s why one needs to perform the same check on different platforms to make sure they are all successful. Library dependencies or platform issues can be identified quickly here. However, the golden checker will not drive the binary file. So the functional checks described in next paragraph will be next step.
Typically, an AMI model have several parameters. To validate a model thoroughly, all combinations of these parameters values need to be exercised. We can “parameterize” settings in a .ami file like below:
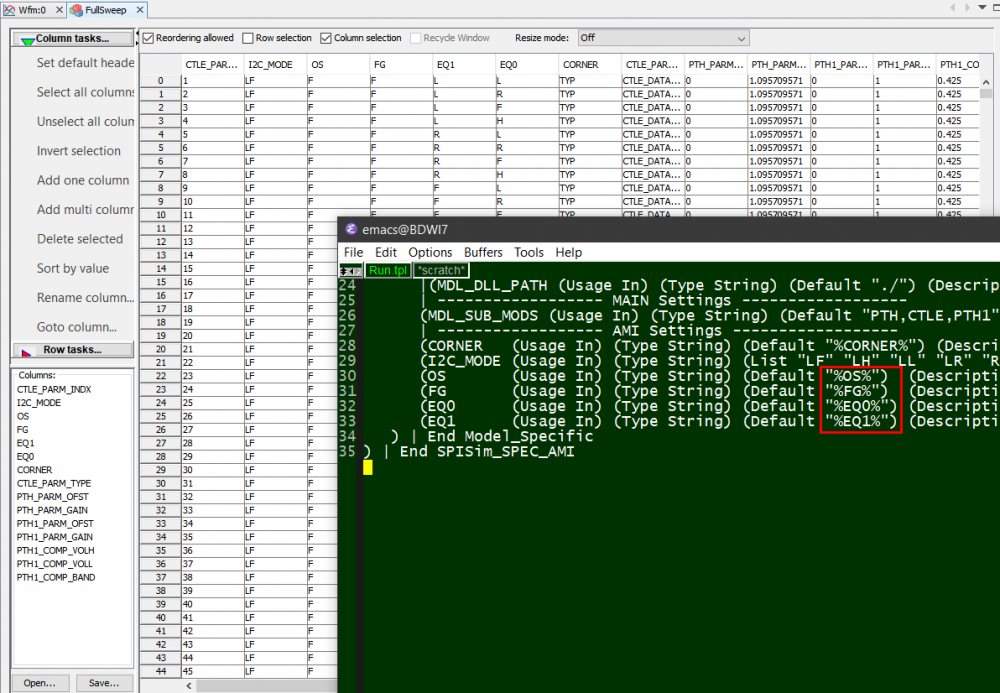
Here, pattern like %VARIABLE_NAME% is used to create a .ami template. Then our SPIMPro can be used to generate all combinations of possible parameter values and create as a table. There can usually be hundreds or even thousands cases. Similar to the process described in “Systematic approach mentioned in my previous post”, we can then generate corresponding .ami files for all these cases. So there will be hundreds or thousands of them! Next step is to be able to “drive” them and obtain single model’s performance. Depending on the EDA tools, most of them either do not have automation capability to do this in batch mode or may require further programming. In our case, our SPIMPro and SPIVPro have built-in functions to support this sweeping flow in batch mode all in the same environment. SPISimAMI model driver is used extensively here! Once each case’s simulation is done, again one needs to extract the performance then compare with those obtained from raw data and make delta comparison.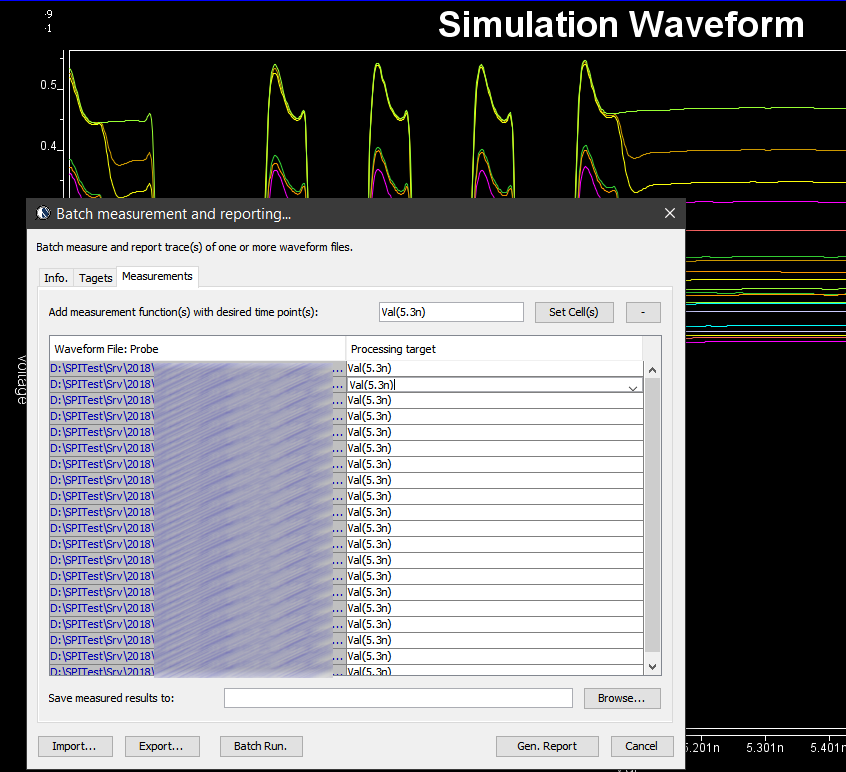
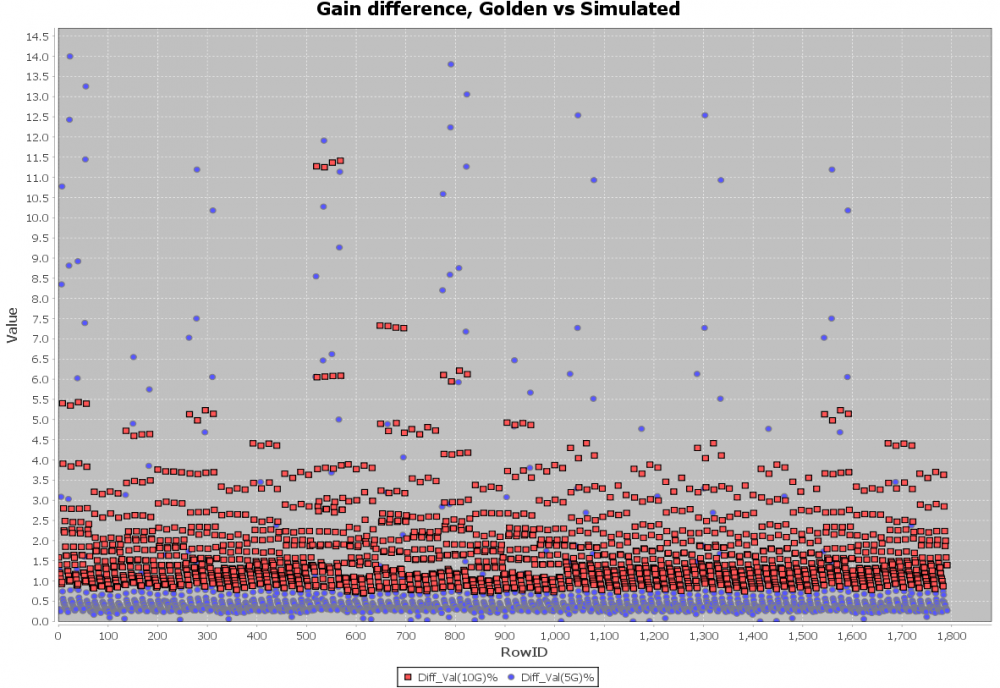
A scattering plot like below will quickly indicate which AMI parameter combinations may not work properly in newly created AMI models. In this case, one needs to go back to the modeling stage to check the codes then do this sweep validation all over again.
Channel correlation:
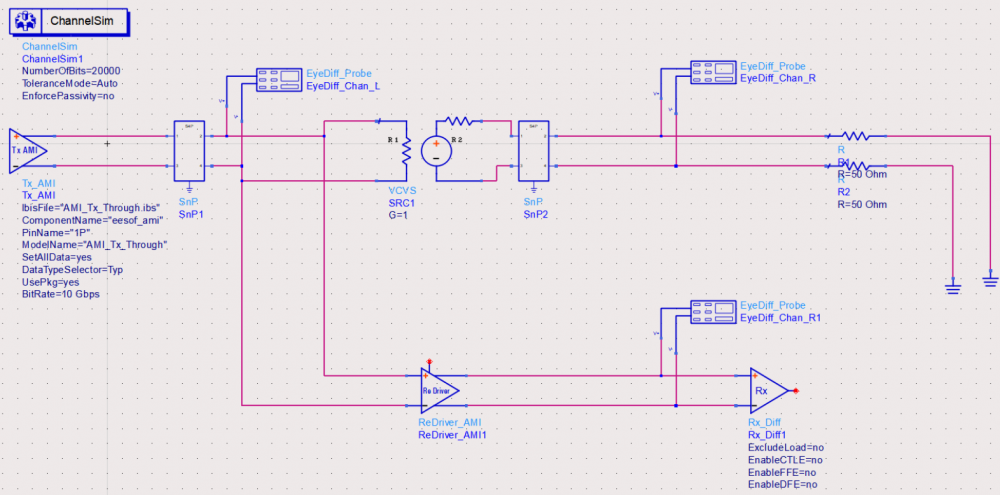
The model validation mentioned in previous section is only for a single model, not the full channel. So one still needs to pick several full channels set-up to fully qualify the models. A caveat of the channel analysis is that it only shows time domain data regardless the flow is “statistical” or “bit-by-bit”, that means it is often not easy to qualify frequency domain component such as CTLE. In this case, a corresponding s-parameter whose Sdd12 (differential input to differential output) is represented by this CTLE AMI settings can be used for an apple-to-apple comparison, like schematic shown below:
Another required step here is to test with different EDA vendor’s tool. This presents another challenge because channel simulator is usually pricey and it’s rarely the case that one company will have all of them (e.g. ADS, HyperLynx, SystemSI, QCD and HSpice etc). Different EDA tools does invoke AMI models differently… for example, some simulator passes absolute path for DLL_Path reserved parameter while others only sent relative path. So without going through this step, it’s difficult to predict what a model will behave on different tools.
Documentation:
Once all these are done, the final step is of course to create an AMI model usage guide together with some sample set-ups. Usually it will starts with IBIS model’s pin model associations and some performance chart, followed by descriptions of different AMI parameters’ meaning and mapping to the data sheet. One may also add extra info. such as alternatives if the user’s EDA tool does not support newer keyword such as Dll_Path, Dll_ID or Supporting_Files etc. Waveform comparison between original data (silicon measurement vs AMI results) should also be included. Finally it will be beneficial to provide instructions on how an example channel using this model can be set-up in popular EDA tools such as ADS, HyperLynx or HSpice.

Summary:
There you have it.. the end-to-end AMI modeling process without touching programming details! Both AMI API and programming languages are moving targets as they both evolve with time. Thus one must continue honing skills and techniques involved to be able to deliver good quality models efficiently and quickly. This is a task which requires disciplines and experience of different domains. After sharing these with you readers, do you still want to do it yourself? 🙂 Happy modeling!
For engineers who are new to IBIS modeling, the “IBIS CookBook” [LINK HERE] is a very good reference document to get started. The latest version, V4.0, was created back in 2005. While most of the documented extraction procedures still hold true to this date, some of them may be tedious or even ambiguous in terms of executions. This is particular true for processes mentioned in Chapter 4, differential buffer modeling. Further more, most recent IBIS summit presentations focus on “new and hot” topics like IBIS-AMI modeling methodologies and not many are for the traditional IBIS. In this post, I would like to first review these “formal” process, dive into how each modeling table is extracted and used in simulation, then propose a “quick and easy” method particular for differential buffer. I will then summarize with and this approach’s pros and cons.
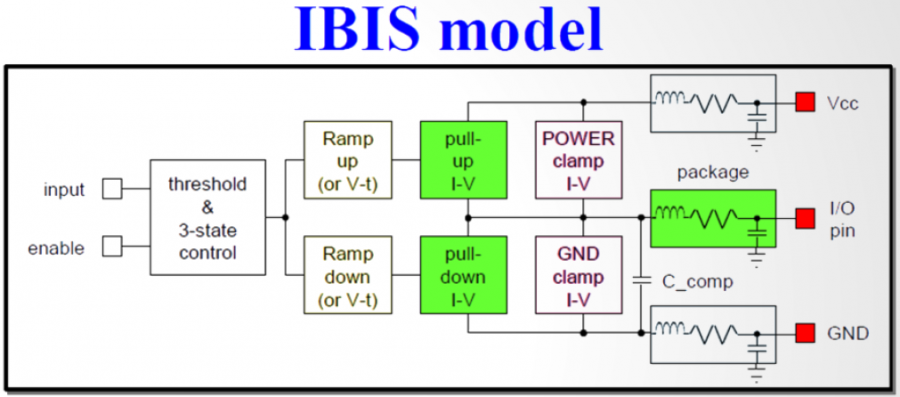
The most basic IBIS building block, as defined in Spec. Version 3.2, is shown above. Typically at least six tables will be included in an output type buffer. They are IV (Pull-up, Pull-down) and Vt( Rising and falling) under two different test load conditions. Additional clamp IV table (Power and Ground clamp) may be added for input type buffer. After Spec version V5.1, Six additional IT tables for ISSO_PU/PD/Composite currents have also been added to address PDN effects. To create an IBIS model, the data extraction processes start with exciting particular portion of the buffer so that measured data can be post-processed to formulate as a spec-compatible table format. Because a model also has TYP/MIN/MAX skews, so the number of simulations are basically the aforementioned number of tables times three. That is, for a most basic IBIS modeling, one may need to simulate at least eighteen cases (or simulation “decks”).
To explain a little bit more regarding blocks untouched by proposed new method, I list them in the bullets below:
The process suggested in IBIS’s cookbook can be summarized as the following steps. They are also implemented in our “Full IBIS modeling flow” within SPIBPro:

Full step-by-step modeling flow in SPIBPro
For a single-ended buffer, the first hurdle in the modeling process is to make sure each blocks are excited properly and simulation results make sense. As mentioned, there are at least eighteen simulation needs to be done:
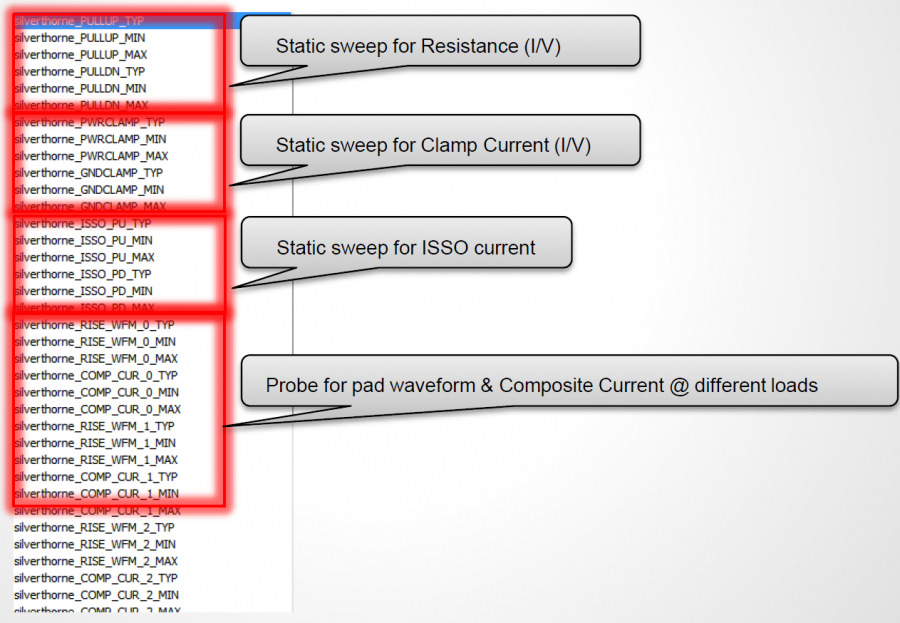
There are also some complications regarding the DC simulation part: some of the buffer may have “clocking” and it’s not easy to separate them from the buffer iteself. Also, there may be many RC parasitics between nodes for a buffer netlist extracted from post-layout. In other cases one can’t even separate the actual IO part from the pre-driving portions and the resulting circuits to be simulated become huge and time consuming. These situations will make IV data extraction slow and often problematic. As a result, a simple step 0~7 modeling process may not work properly and one need to iterate to tune the set-up such that simulation will always converge and resulting IV curve be monotonic. Nevertheless, the single buffer’s modeling is easier to manage.
Differential buffer’s IBIS modeling extends the challenge and effort to another dimension…literally! First of all, each pin in an IBIS file or component connect to an IBIS model and the possible structures and connections between different pins are very limited. So for a differential buffer, a series element needs to be created to describe the coupling relations between pins. All the pictures used in this paragraph are from IBIS cookbook and user may find further descriptions there.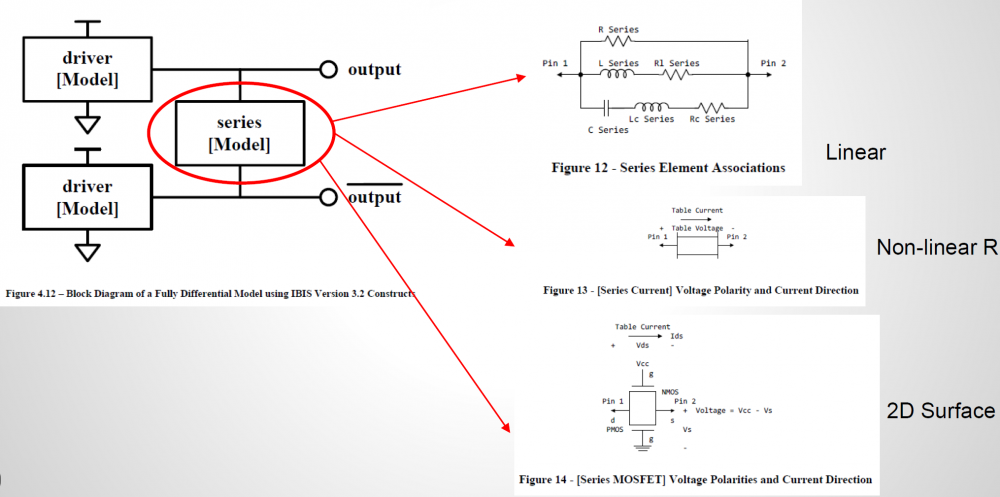
In order to construct such series model, the IV sweep needs to be performed in two dimensions, both at similar resolutions. So if say a typical single-ended IV curve has one hundred points, then the second dimension should also have that much data. That means for one particular corner, there will be one hundred IV simulation in order to construct the 2D response surface shown below. First stage post-processing also needs to be preformed so that common-mode current can be eliminated. All these need to be done before formulating a 2D data view. Only after one can visualize the resulting data, he or she can determine what components are needed to create such series model. This presents the first challenges on top of the IV simulation issues mentioned for single-ended buffer.
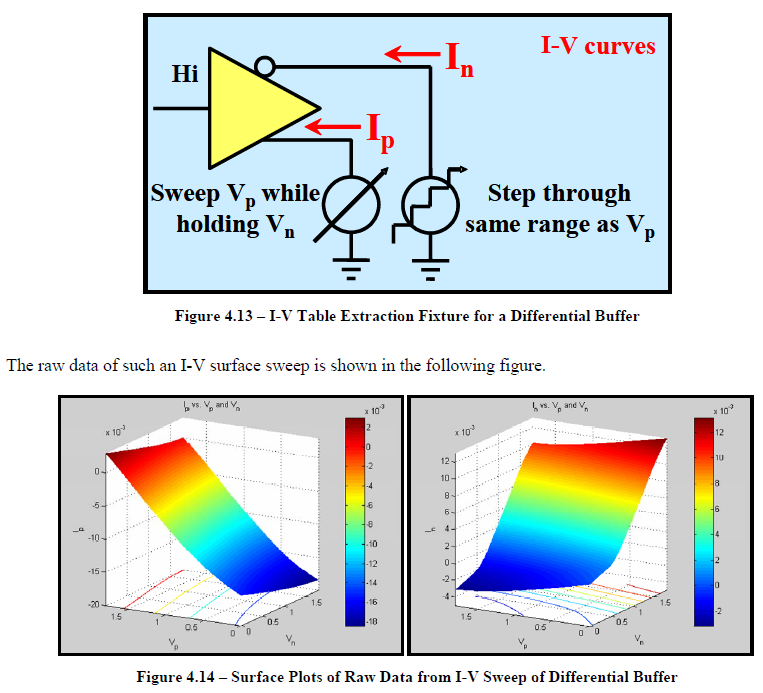
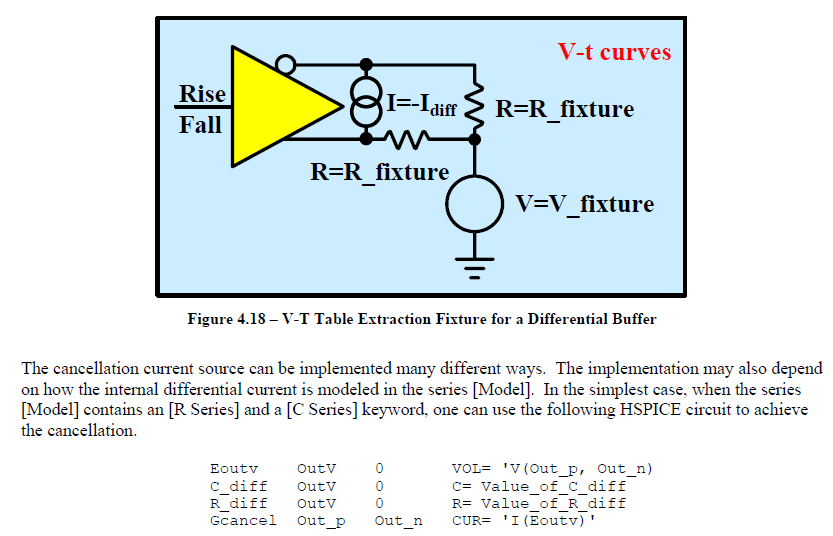
The second challenge is regarding the VT simulation. The current flow through this newly constructed series element needs to be “eliminated” to avoid being double counted. For spice-like simulator, there is no such thing as “negative resistance”, “negative capacitance” etc. So one has to resort to approaches like control elements or even Verilog-A (as we presented in IBIS Summit 2016) to have proper VT data extracted. For control-source based approach, it is only limited describe pin couplings of a simple R/C but not non-linear resistance or surface such as series mosfet. For that, an intermediate step to map device or equation parameters to the calculated 2d surface is needed. Even using Verilog-A’s look-up table, the grid resolution is limited by the step size used in first two-dimensional IV step and may have non-convergence issue if it’s to coarse. That’s why in the cook book (the first two lines in the picture below), it doesn’t suggest any approach as it’s really not that easy!
Due to these two great challenges, we have found that differential modeling may not be easy for most modeler. We feel more this way when providing modeling service to clients who wants to perform simulations themselves then send us data. They may want to do so due to IP concern or they knowing more about the design. In those cases, the back-and-forth tuning and tweaking process become a burden on their side and also delay the whole schedule. Thus we are motivated to find an alternative “quick-and-easy” approach to substitute the “formal” modeling steps mentioned above. While being able to simulate accurately w/ great performance is still number one priority, we are ok that they can only be used under some context (such as channel simulation).
In previous post, we explained how IBIS model’s data are used in a circuit simulation. Simply speaking, the “VT” data is considered as “target” while “IV” tables are used to compute so called “switching coefficients” so that appropriate amount of current will be injected or withdrawn from the buffer pad to achieve. When this is true, the nodal voltage specified by that VT table at that particular time point will be satisfied due to KCL/KVL. Now there are switching coefficients for both pull-up and pull-down structures… thus it takes two equations to solve these two unknowns. That’s why two set of VT, each under different test loads, are required. Based on this algorithm, an IV data and calculated coefficients are actually “coupled” and affect each other. If current in IV table is larger, than the calculated coefficients will become smaller and vice versa. This way the overall injected/withdrawn current will still meet KCL/KVL required for VT. In this sense, the actual IV data is not that important as it will always be “adjusted” or “weighted” by the parameters.
On the other hand, the VT data also contains several DC points and they need to be correlate to the IV table, otherwise DC mismatch errors will be thrown by the golden checker. In addition, the IV data is limited to 100 points and they need to be monotonic to avoid convergence issue. So if we have several sets of VT data and one under normal test load (say 100 ohms for a differential buffer), then they will give us “hints” regarding how IV data will look like.
With this assumption, we propose the following quick-N-easy modeling steps:
And that’s all, through carefully implemented algorithm and computation, we can generate an IBIS model based on these data with minimal simulation requirements. An the generated model is guaranteed to be error/warning free.
While we will not disclose how these are actually done in details, we can show how they are incorporated in our SPIBPro… as shown below. As a matter of fact, this process has been used in the modeling projects of past year and shown great success.
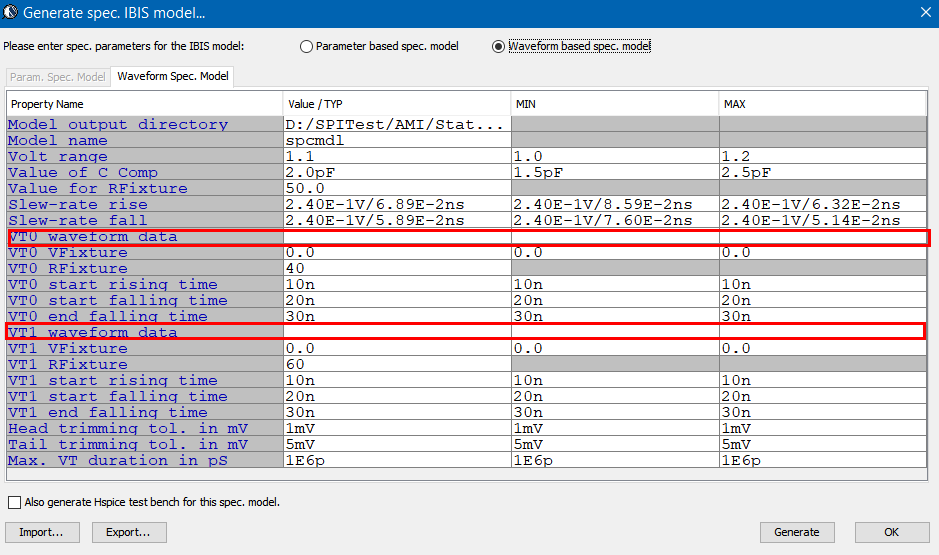
Only two VT simulation data are required to create an IBIS model
We use this approach to create differential IBIS for channel analysis purpose (together with AMI) and have not yet found any problems. Having that said, I would offer several pros and cons for reader’s considerations:
Pros:
Cons:
In this blog post, we reviewed the formal IBIS modeling process described in the cook book, challenges modelers will face and proposed an alternative “quick-and-easy” approach to address these issues. The proposed flow uses minimum simulation data while maintaining great accuracy. There might be limitations on models generated this way such as neither disable state nor power-aware data are accounted. However, in the context of channel analysis particular when a differential model is used together with its IBIS-AMI model, we have found great success with this flow. We have also incorporated this algorithm to our SPIBPro so our tool users can benefit from this efficient yet effective flow.
Preface:
We SPISim recently developed and released free web apps for various channel analysis tasks [Click HERE for overview]. While their product page each gives good descriptions and demo about what each tool can do individually, we think it will also be beneficial to put them all together in one flow so that user may have better picture about our ideas behind these developments. Thus this post is written for dual purposes: First we would like to explain how a channel analysis is usually performed. Secondly we want to show how one can perform such process using apps even directly from the web browser. Just for comparison, creating AMI models and license for this type of simulator usually costs tens of thousands of dollars up front. Now it can be done for free!
The big picture:

[Fig. 1, A SERDES system]
Let’s use a SERDES system, shown in Fig. 1 above, as an example. For other interface’s such as DDR, please see our previous blog post for considerations about similar application.
A SERDES system uses a point-to-point topology. In Fig. 1, the middle block enclosed in blue represents the channel. It mainly contains passive interconnect such as package, transmission line, vias, connectors or even cable. However, the channel may also include active components such as Tx and Rx devices. These active components are usually represented by IBIS or spice models. Alternatively, we can pull these active components out from the channel and “merge” them into the EQ as “analog front end” stages. In that case, the channel become pure passive. One of the reasons why one may want to do it this way may be either that the IBIS models are not be ready, or there are no simulators available to have them included as part of the simulation. This is usually the case when a free spice simulator is used as none of them that I am aware of supports IBIS out of the box. In general, unless analog front end AMI models and a pure passive channel, represented as a S-parameter, are used together for the analysis, the active devices do need to be part of the channel characterization in order to obtain accurate time domain response.
The next step is to obtain or generate AMI models for each Tx and Rx EQ circuits. Interested reader may refer to several posts we have written about possible software architecture and methodologies.
Regarding the channel analysis process, a simulator will first convert the characterized channel in s-param, or step response into impulse response first, then depending on the simulation mode being specified, this response or convoluted bit sequence will be fed into Tx and Rx respectively to obtain the overall response. For LTI system, a permutation process will be performed for all possible bit combinations to calculate the PDF of each sampling point statistically, then integrate to obtain the CDF and thus create a bath tub plot. For a NLTV system, bit-by-bit waveform is accumulated and overlapped to plot the eye and BER may be extrapolated from there. While not mentioned here and also not yet implemented, various jitter and noise components are also important when creating the stimulus or calculating final results.
Following the analysis procedure detailed on Section 10.2 of IBIS spec, to summarize them briefly, a channel analysis includes three tasks: channel characterization, EQ model creation and putting them all together for channel simulation.
Task 1. Channel Characterization:
The first step of channel analysis is to characterize the channel, the blue block of Fig. 1, in order to obtain is time domain response. Even with active Tx/Rx front end being involved, the assumption here is that the characterized response will be linear time invariant (LTI). With a LTI input, a channel simulator can either perform statistical analysis if other EQ components are also LTI, or it can have the impulse convolved with PRBS bit sequence to generate full time domain waveform, finally procees to process with NLTV EQ components to get the final time domain waveform for further eye analysis.
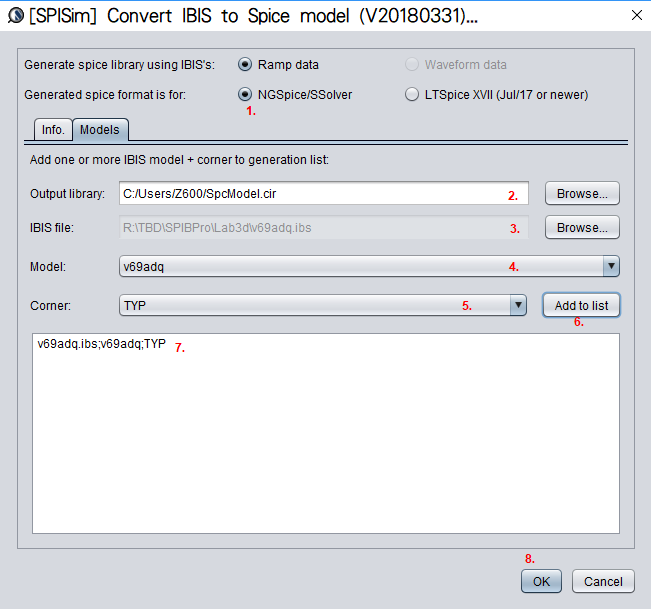
If the passive channel is from post-layout, then user will need to use other 3D extraction tool to obtain the interconnect’s s-parameter. Devil’s details here will then include making sure the S-parameter is in good qualities such as being passive, causal, symmetric and asympotic etc. Also depending on the simulator, converting the single ended s-parameter to mixed-mode/differential one may also be needed. On the other hand, for pre-layout case, user will then first obtain or generate each component’s simulation model. Assuming what user have here are Tx and Rx IBIS model, transmission line and other R/L/C based behavioral models for package, via and connectors, then first one can use our [SPISim_IBIS web app] to convert those IBIS model into free simulator compatible spice subcircuits:
Then head over to LTSpice, offered by Analog device, to download and install the free simulator.
Either create schematic or a text netlist of the channel them perform a transient simulation to get its step response. The output will be a raw file in compressed format which can be viewed either in place in LTSpice or use SPISim’s free SPILite: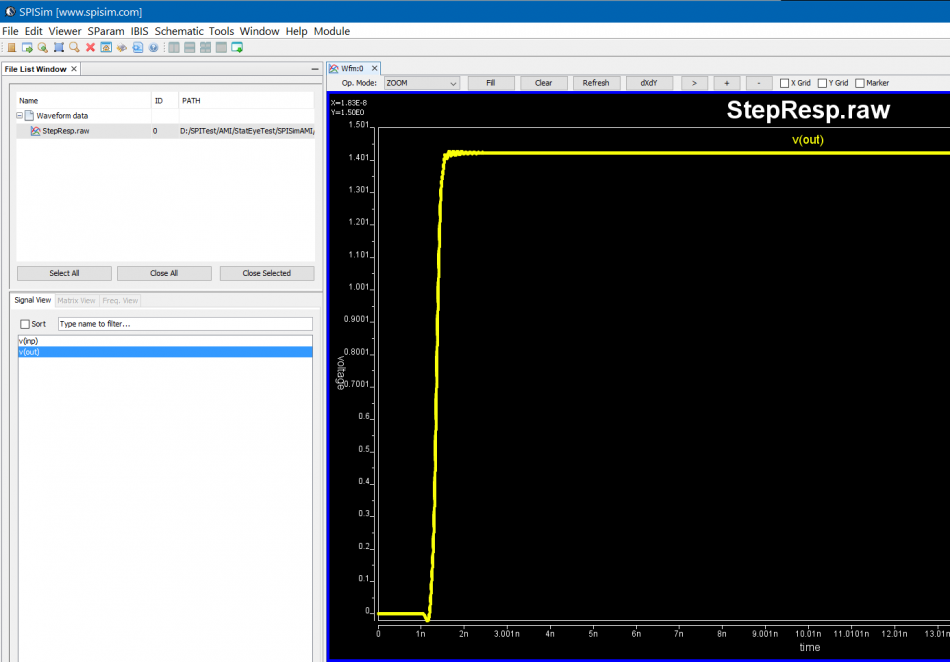
Task 2. Tx/Rx EQ Modeling:
If no EQ circuit is involved, then user can simply tinker the circuit/simulation settings completed in task 1 to perform conventional time domain based SI analysis. The reason stat-eye like channel analysis comes to play is because EQ circuits (represented in green block for Tx EQ and orange block for Rx EQ in Fig. 1) are involved to open the eyes and many more bits need to be “simulated” to obtain/extrapolate low BER, thus can’t be done easily using nodal based spice simulator as it will simply take too much time. EQ circuits can come in different models such as behavioral, spice or AMI, with AMI being the common denominator supported by almost all channel analysis tools from different vendors. Thus in the second task, we need to generate IBIS-AMI models for Tx and Rx EQ.
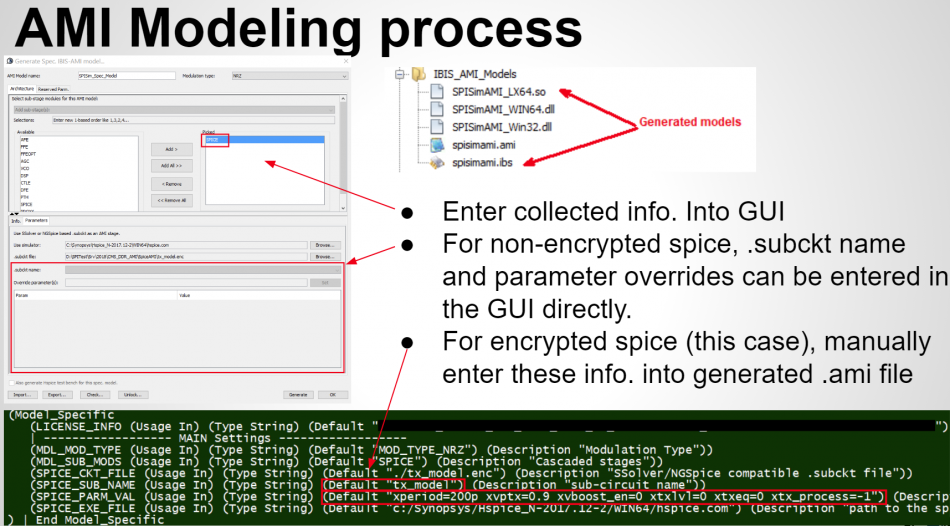
IBIS-AMI modeling usually involves C/C++ coding or compilation into .dll/.so if starting from scratch. However, user may use [SPISim_AMI web app] to generate AMI models instantly without going through those steps: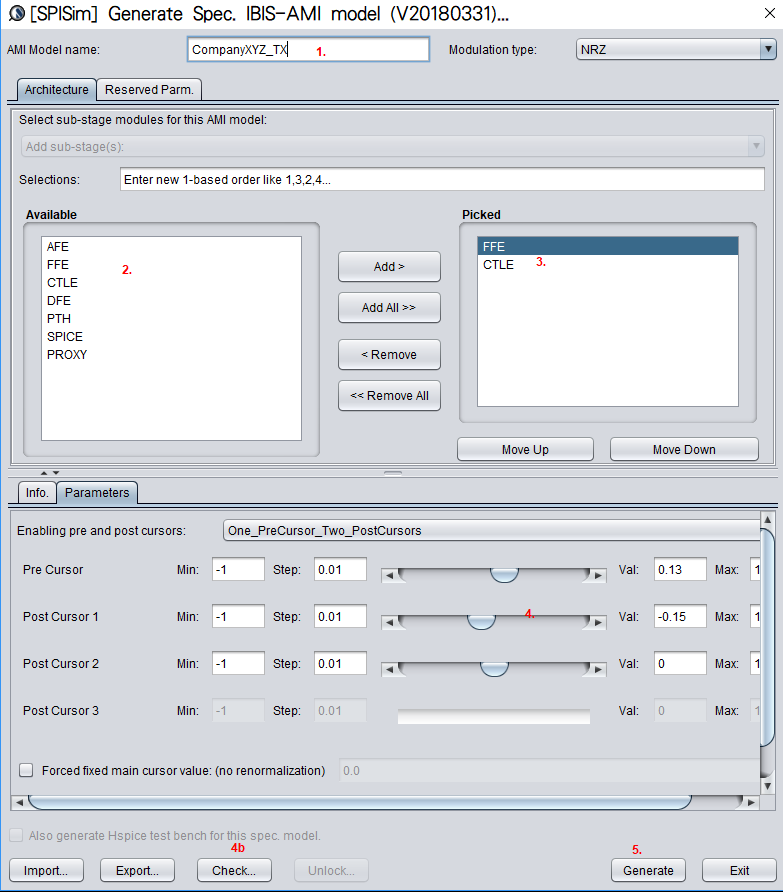
Test driving the model and view its response in place to verify the model’s parameters meet the performance needs: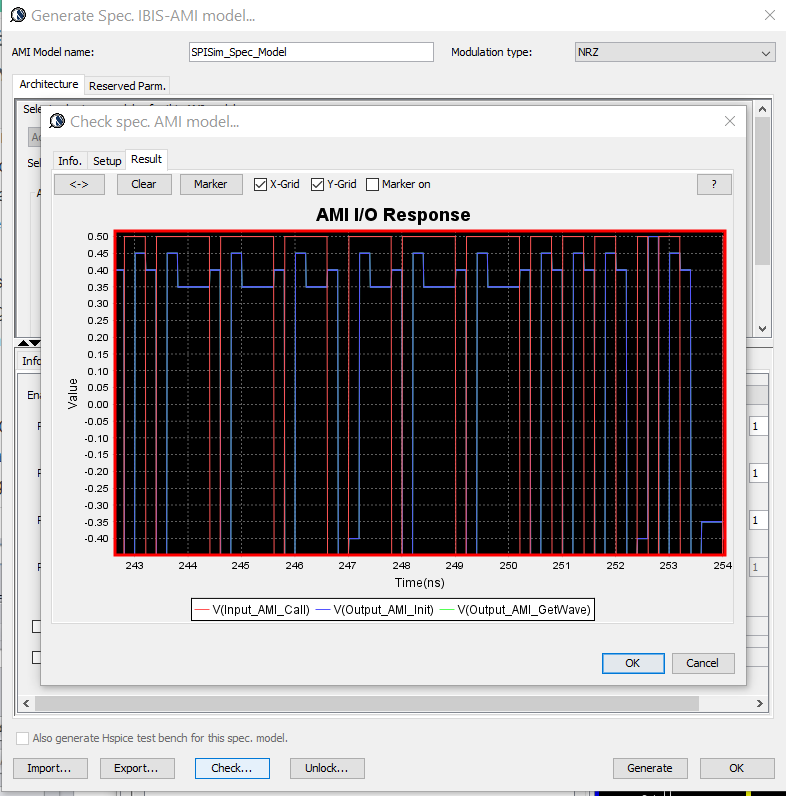
Then click “Generate” button and the AMI model will be generated instantly. If cross platform models are desired, use [SPILite] instead and all Windows 64, Windows 32 and Linux 64 models will be generated in one shot.
At the beginning of this section, we mentioned that the EQ model can also be in the form of spice circuit, whether encrypted or not. In that case, its detailed behaviors will not be able to be described exactly by template based or pre-defined models. However, a spice wrapper AMI model supported by SPILite can still be used, it will make this spice model “AMI compatible” and can be used in other channel simulators. User’s licensed/installed simulator will be called during the channel simulator.
Task 3. Channel analysis:
With both Tx/Rx EQ models plus channel response being ready, we can then perform the StatEye based channel analysis using [SPISim_Link web app]:
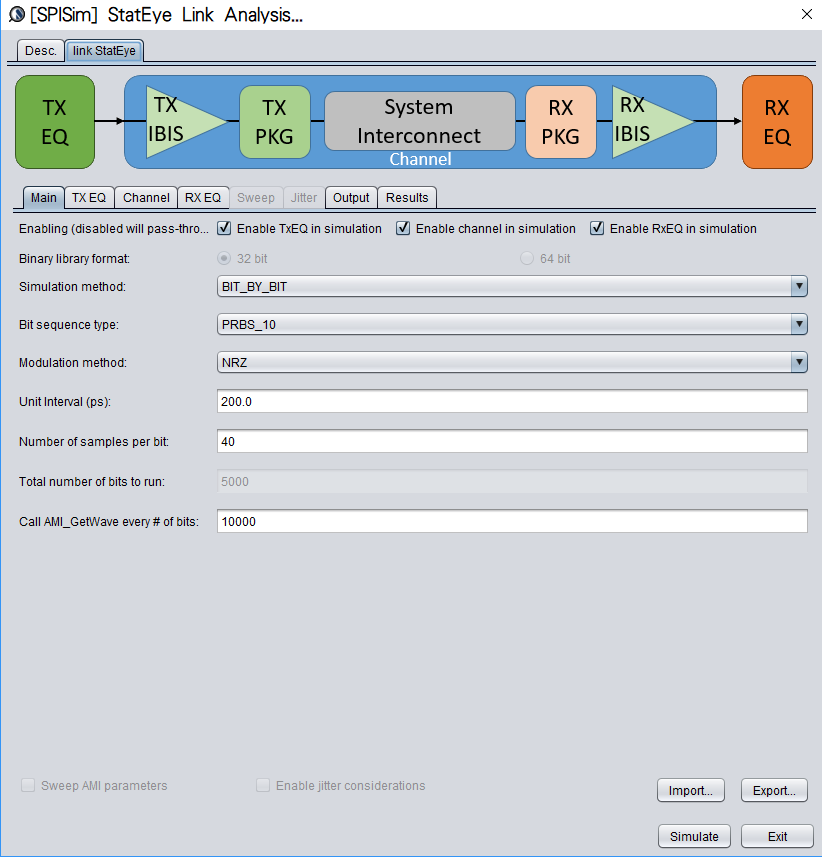
Detailed usage about this tool is demonstrated in a video on its product page. Basically, user can specify the generated AMI models in the “Tx EQ” and “Rx EQ” tab respectively, then do the same for the step response waveform to the “channel tab”. Both “statistical” mode and “Bit-by-bit” modes are supported here, yet if NLTV EQ such as DFE is used in part of the receiver, then “statistical” model can not be performed. With these set-up ready, a “Simulate” click will show the results in place within seconds:
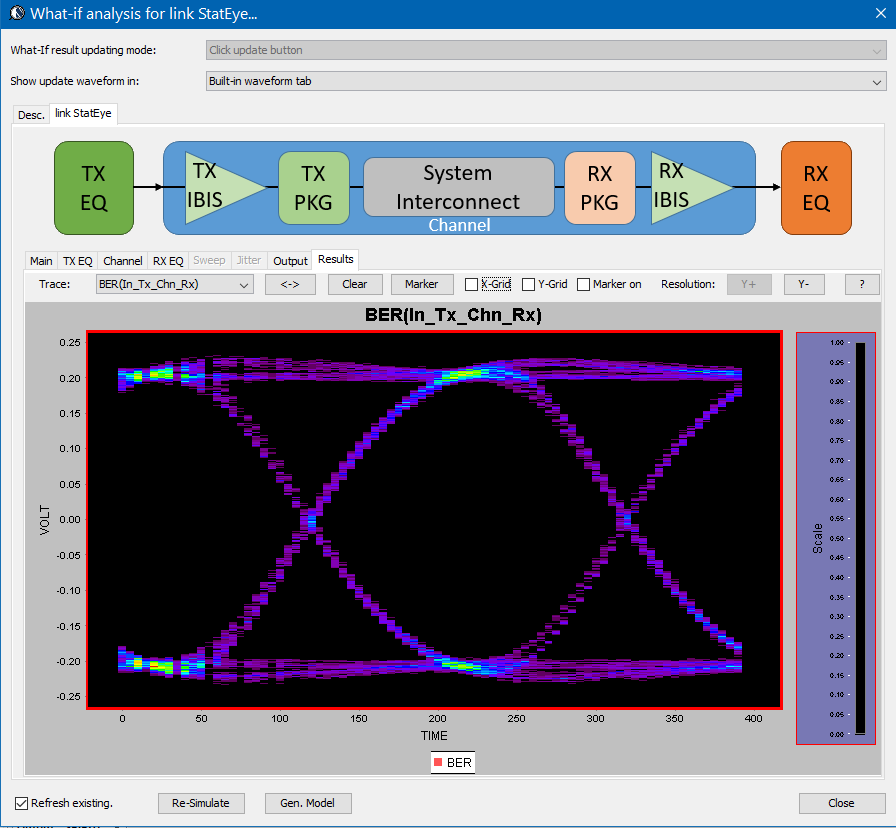
The bath tub curve representing the CDF is also ready for inspection/eye measurement: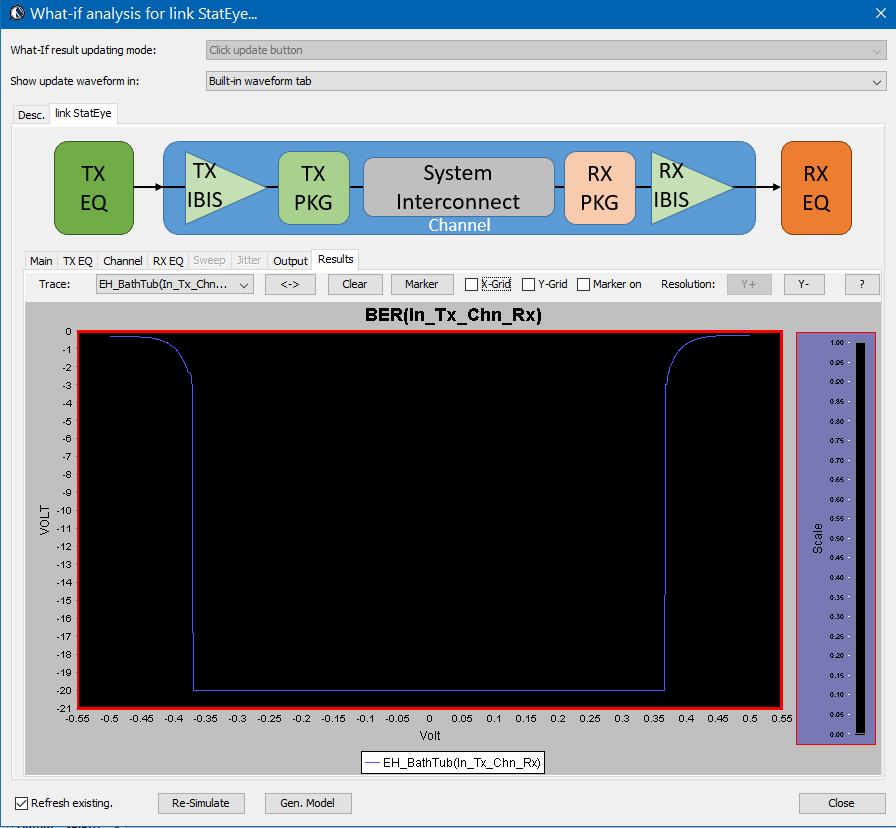
Alternatively, task 1 and 2 are also directly supported in the SPISim_LINK function alone so user may choose to experiment with different settings and see their response first before generating corresponding AMI model. For example, a simple change of post-tap value in Tx can be done in the UI: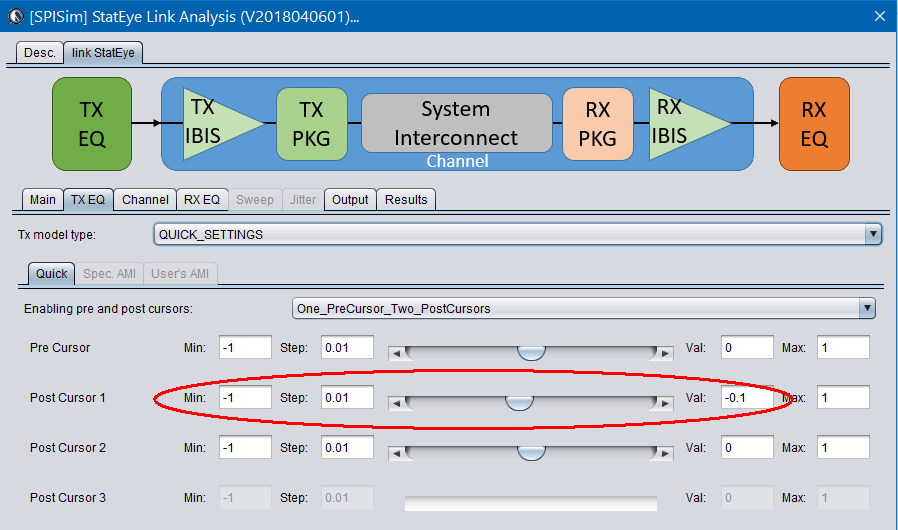
Then the re-simulation will quickly show its effect in resulting eye: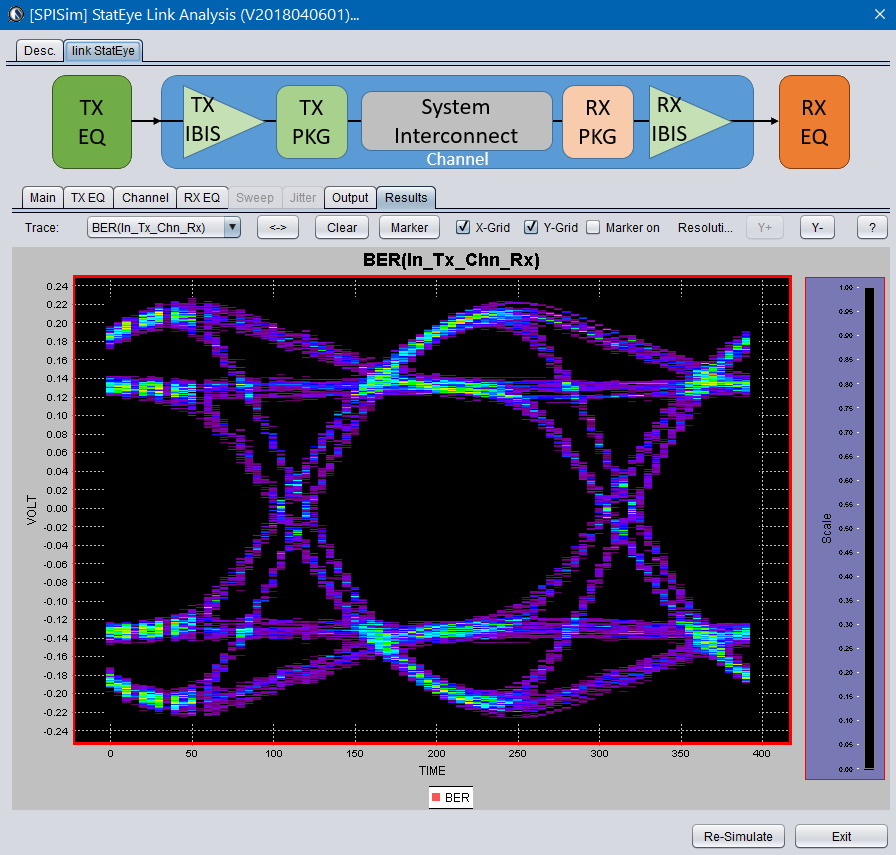
For a system developer, he/she may obtain corresponding AMI models from their IC vendors and follow the same process to give these model a try. For an IC vendor, the AMI model generated here will also be compatible with other vendor’s tool and you may provide these models to your system clients before committing to perpetual version of the model.
Here you have it…. an economic yet efficient channel analysis which can be done directly through the web has been enabled for your design needs without any cost!
[This blog post is written in preparation for the presentation of the same title to be given at the 2018 DesignCon IBIS Summit. Presentation slides and audio recording are linked at the bottom of this post.]
An AMI model is in the binary form of .dll (dynamic link library) or .so (shared object). It itself is not an executable and can’t be used directly. To load or run the AMI models, one needs to have a “driver”. Commercial tools like HSpice has a license required utility called “AMICheck” to test drive the given AMI models with rise/fall/single bit response. We SPISim also provide a free utility called SPISimAMI.exe which does pretty much the same. These small drivers are good when you want to quickly check whether the AMI models at hand are “run-able”. However, to validate or test model’s full function, such a simple tester is often insufficient. In an ideal situation, a link analysis simulator, which will load Tx and Rx AMI models involved and perform calculation/optimization, is preferred as a driver. If a model developer can use IDE to attach to this simulator process and have access to the simulator codes as well, then he/she can set a break point within both simulator and the loaded AMI model to step through and debug during the whole analysis process.
Even if one doesn’t have access to simulator’s codes or debug build, theoretically, an IDE can also “attach” to a process before it loads the AMI dlls in which we have break points set (as a model builder, we have access to the model codes). However, thing is not so straight forward in real world. Most of the EDA tools I have seen allow user to interact different link analysis settings via GUI, then when a “simulate” button is clicked, a separated process is launched/forked and that process will do the work such as characterizing channel, loading AMI models and simulation etc before giving results back to the front-end GUI for further display. It is not easy (if even possible) to automatically attach dll files being debugged to these “spawn/forked” process. No to mention that if both Tx and Rx models are involved in a optimization process (such as back-channel), then simply stopping at a breaking point within one of the AMI models is not enough… one can’t observe and see the interactions for full picture. With these limitations, develop and testing AMI models within a full link analysis flow become challenging.
For a model developer who does not have access to these full link simulator’s sources, open source platform is a direction. There are several ones out there already… PyBert and COM are two such examples. From what I have seen, most of them already have some generic Tx/Rx algorithm blocks in place. So these EQ operating portions may be replaced to support AMI models to meet our needs. Being able to do so will shorten the model design cycle and enable the possibility to develop blocks with more advanced capabilities (such as back-channel communication). As PyBert already has some sort of AMI modeling support, this paper intends to explore possibilities to add similar capabilities in IEEE 802.3 spec. supported channel operating margin (COM) flow.
Channel Operating Margin (COM) is a ratified IEEE802.3 spec. Interested reader can find an overview slides given by the COM main author (also my former colleague at Intel) linked here: [Channel Operating Margin Tutorial] More detailed technical details are available in the IEEE 802.3BJ spec document and Richard’s 2013 DesignCon paper of same title. Further more, its matlab source codes are also available at the 802.3 website.
Given such technical depth like COM’s, to describe it in several paragraphs in this post will not be meaningful. So I will try to just give an overview from AMI builder’s perspective and help reader to see how AMI models can be plugged-in to the flow.
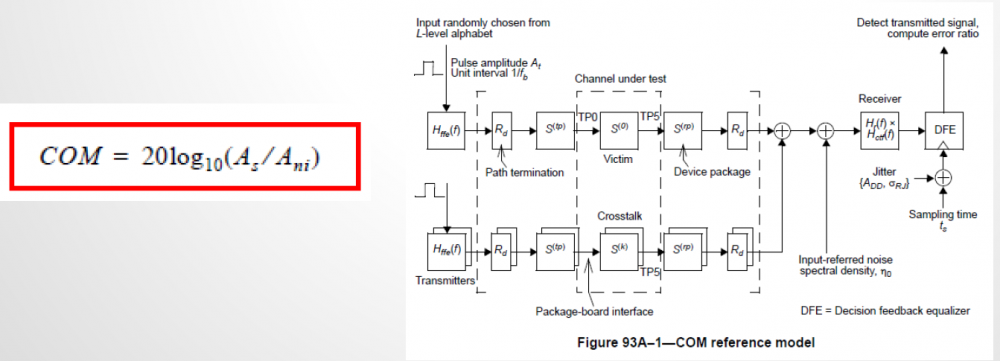
COM’s reference model is shown above. The upper half of the right side represent the through inter-symbol-interference (ISI) channel and the lower half is for the crosstalk (XTK), which can be near end, far end or both. Simply put, COM is an evaluation of signal to noise ratio for the full system. Most of the noise terms, such as mentioned ISI, XTK, jitters etc have all been taken into account. The signal part is the peak of the single bit response (SBR, i.e. pulse response). COM itself has published algorithms for many different blocks above and also interface specific default parameters for different 803.2 interfaces. EQ portion such as FFE in Tx, CTLE in Rx and even DFE are also implemented.
For a SERDES designer or AMI model builder, channel S-param (with or without package portion) is assumed given and COM flow will select best selection of FFE tap weights, CTLE pole/zero location and DFE tap weights as well. The searching flow for these parameters are exhaustive… full combination of FFE taps and CTLE dc gains are used to apply for toward the channel. A figure of merit (FOM) is then calculated for each combination. Best case is then decided based on the FOM value. Once EQ settings have been decided, then a SBR is formed and a full blown BER like analysis is applied with DFE involved to calculate final COM value.
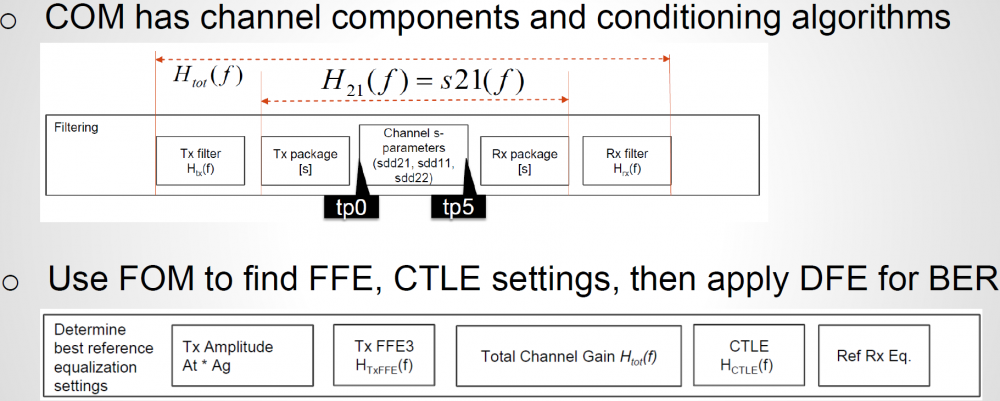
For a link analysis flow, the first step is to “characterize” the channel, i.e. obtain impulse response. There are many devil’s details behind this step… single-ended s-param may be need to converted to mixed mode, package models of different sections needs to be cascaded, and finally the cascaded s-param needs to be “conditioned” before doing IFFT (not using an IBIS model or analog front-end in COM). All of these are important yet may be out of an AMI model builder’s direct concern… then just want this channel to “work”. Fortunately, these steps have all been included in COM flow already and can be used as they are.
Regarding Tx and Rx EQ, original COM implementation (circa. 2014) only supports one FFE pre-tap and one post-tap for TX. Recently, it have been extended to support two pre-tap and three post-taps. For CTLE, two poles and one zero equation is used and user can only sweep DC gain. The analysis flow is very similar to what’s described in IBIS spec section 10.2 but only with LTI assumption. That is, impulse response obtained from conditioned S-param is sent to Tx EQ, then pass through Rx CTLE before further processing. DFE taps are not optimized within each iteration of FOM calculation, it’s calculated only after optimized FFE + CTLE settings have been found.
As mentioned previously, the searching algorithm of these EQ is exhaustive. So if one open the published COM matlab codes, he/she will find the multi-level loops for different Tx EQ taps and Rx CTLE Gdc settings as shown above. To replace these generic EQ functions with our AMI models, codes need to be changed here.
To use AMI model in a COM flow, one need to replace collect the replace these FFE and CTLE calls in the COM codes with the corresponding AMI model invocation. Here shows two possible modifications routes:
The first step is to “combine” or “collapse” those multi-level loops into single loop. This single loop can be iteration which go through an array which contains all the AMI parameters combinations to be tried (may not be exhaustive) or has a “stopping-criteria” which will “break” the loop such as optimization within this single loop has reached solution. Tx and Rx may not be FFE/CTLE respectively or can have different format (for example, CTLE can iteration list of frequency response curves rather than pole/zero data). For the later case (optimization), Tx and RX can be calculated together if needed. original COM’s package length and DFE can still be used to calculate FOM of different condition if needed.
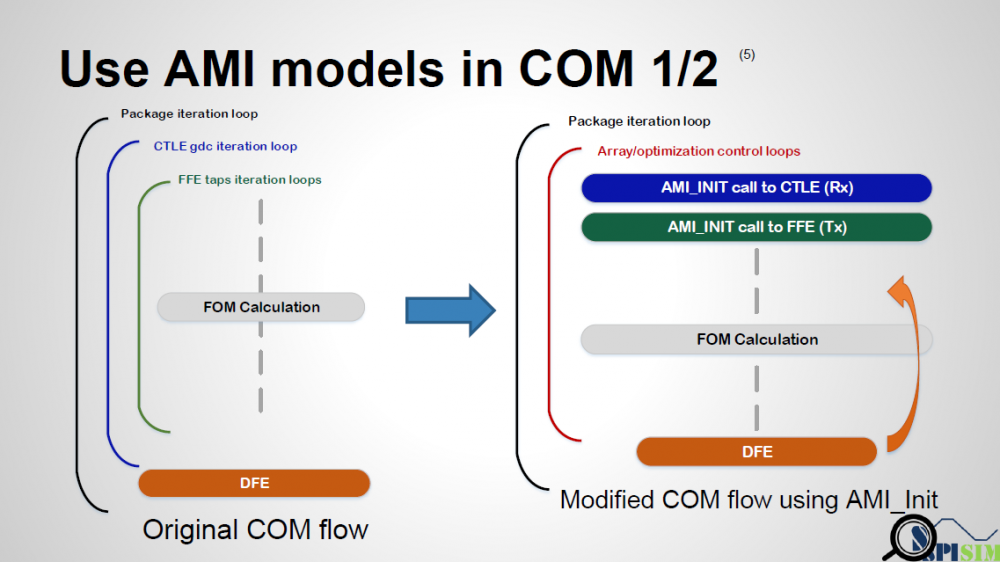

Regarding implementation details, as COM was originally written in matlab, so matlab’s corresponding mechanism to load and call external DLL functions need to be used to replace original FFE/CTLE function call. Basically (as shown in the right part of the picture above), mex -setup needs to be called to determine which IDE environment is installed in the working computer. A header file which include the definitions of the AMI API function is also needed. Then the following functions are called in sequence:
Also worth mentioned is that if we are doing this for AMI models being developed, not a generalized AMI-capable link simulator, then parser for .ami to form parameter tree is not necessarily needed to form argument passing into ami_init functions etc. We can form a string of parsed “key-value” pairs in advance manually and pass into AMI function. Other open platform like PyBert does have AMI parser built-in for its AMI capabilities.
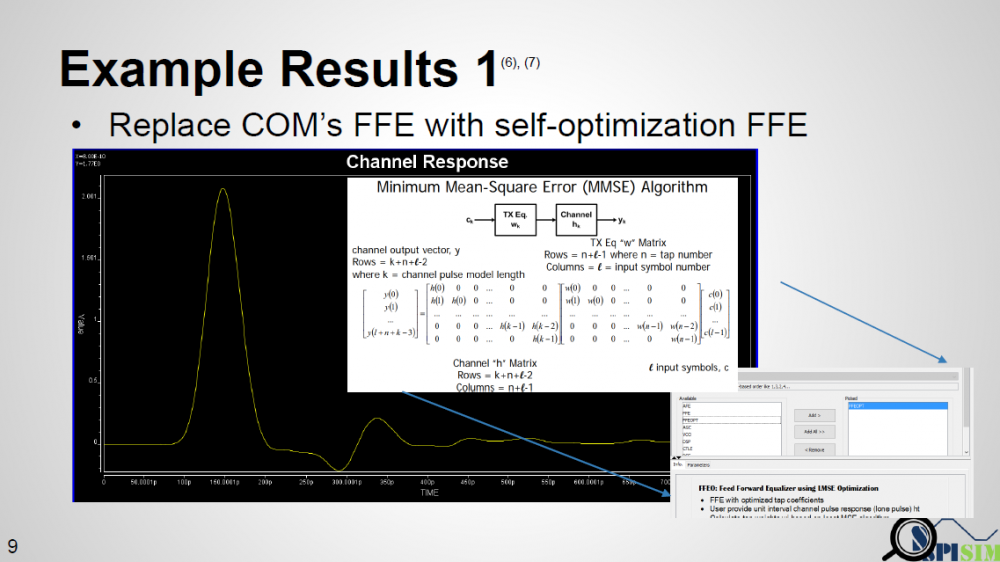
In our experiment, we want to avoid the multi-level loops for all possible FFE tap weight combinations by using our AMI FFE model capable of self-optimization. The concept is simple: if we already have an channel’s impulse response, then the optimal weight to obtain same output as input (recover signal) in the minimum mean-squared error sense can be solved by using pseudo-inverse and linear algebra technique. We want to validate this approach work and can find similar (if not same) solution comparing to full exhaustive search.
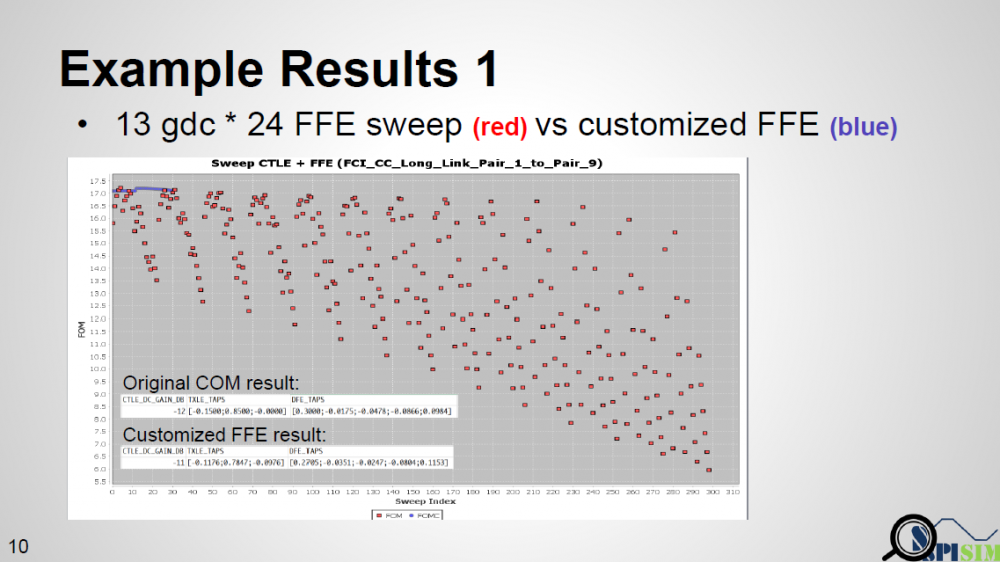
Result is shown above. Red dot represents original COM’s sweeping results (FOM value). There are 13 Gdc values each with 24 one pre-tap and one-post tap combination possible… so total 312 run is needed. Blue dots are our AMI results… since we still use COM’s CTLE, so 13 run is performed. However, for each Gdc run, AMI model computes only once based on the self-optimization algorithm mentioned and finally report best results together with best CTLE Gdc. As seen that blue dots are almost at the top of all 13 original ” COM chunks”, we validate that this algorithm/our Optimization-capable FFE does work.
To summarize this study, first we want to emphasize that for a model developer, who can be an individual model provider or a SERDES designer being asked to develop AMI models, a full flow capable of being used to debug AMI model being developed is needed. This can’t be covered by the simple utility driver particular when optimization such as back-channel come into play.
To meet our needs, open-source link-analysis platform is worth considering. In particular, COM flow of IEEE802.3 is attractive because it’s been ratified, well documented, widely used and support BER-like flow with source codes. While its Tx and Rx block functions may be generic, it’s not difficult to replace those function calls with our own AMI models’ API functions in either LTI or NLTV scenarios. This process not only help shortening model development cycles, but also is very beneficial in further understanding how link analysis is actually performed.
Presentation: [HERE] (http://www.spisim.com/support/paperetc/20180202_DesignConSummit_SPISim.pdf)
Audio recording (English): [HERE]
Here at SPISim, we provide AMI modeling service in addition to the developed EDA tools. Companies interested in AMI service are mostly IC/IP vendors. They need to provide AMI model in particular so that their user, system companies which use their ICs, can perform the design and analysis. Oftentimes, our client is only interested in AMI modeling for either Tx or Rx circuit because that’s where their IC design resides. However, they also often found later on that in many scenarios, it actually takes “two” models to be useful for their users. In this post, I will talk about some of such “paring-off” cases so that interested reader may be well informed when such modeling needs arise.

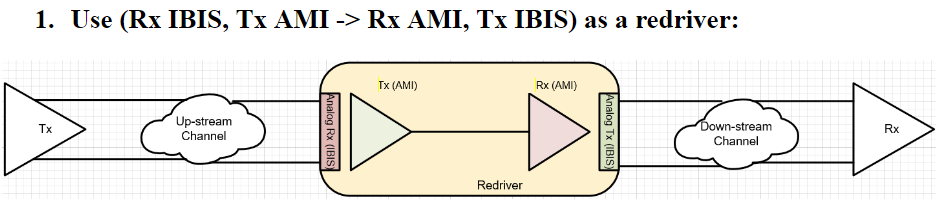
The topology shown above is most commonly used for link analysis. At the Tx and Rx ends, user often is asked to specify corresponding IBIS models. Most definitely, they need to specify AMI model and associated AMI parameters. The interconnect in the middle is generalized here… it can be Tx package, main route, connector and Rx package etc represented in either separate models or cascaded S-parameter. The whole purpose of interconnect here is to provide an impulse response so that when link simulator is operating in either “Statistical” or “Bit-By-Bit” modes, AMI models at the Tx and Rx ends will be able to process accordingly. The analysis flow an AMI-compatible simulator should follow is described in details in section 10.2 of the IBIS spec. User should find that in those descriptions, and almost all the tutorial documents on-line such as the one below from KeySight, both Tx and Rx AMI models are both required to be part of the analysis.
Thus, the first “paring-off” in AMI modelings is each Tx needs an Rx AMI models to work… at least mostly. From this perspective, this is very different from traditional spice-based simulation, where you may have Tx/Rx part in either IBIS, transistor circuit or behavior/Verilog-A modeling format and can simulate without any issue.
So what if you have only either Tx or Rx AMI model? It will be tricky (depends on the simulator) if not possible in many cases. So we here at SPISim often have to provide a “dummy” AMI model in additional to the one ordered. As a “dummy” model, it is a simple pass-through without doing anything. When combined with pass-through S-param or interconnect, it will be very straight forward and clear to test and validate delivered AMI model’s performance. When all the spec. are met (e.g. EQ levels), then the user can add real interconnect and Tx/Rx AMI models from other vendors to proceed the design process.

(A pass-through “Dummy” AMI model implements AMI API but without any implementation body or just don’t change those variables passed by reference)
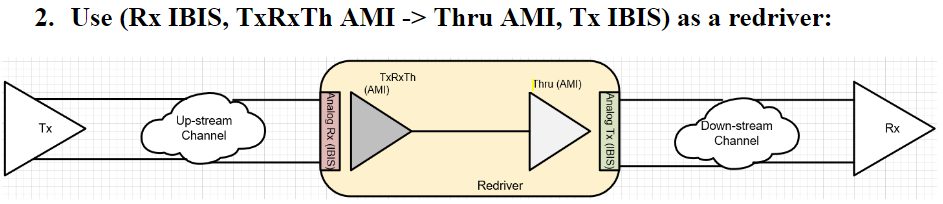
IBIS version 6.0 includes technical advances such as mid-channel repeaters documented in BIRD 156.3. Repeater is often used in longer SERDES channel such as PCIe or HDMI etc. There are two types of repeaters: redriver and retimer.
It’s easy to see the “paring” part within a repeater: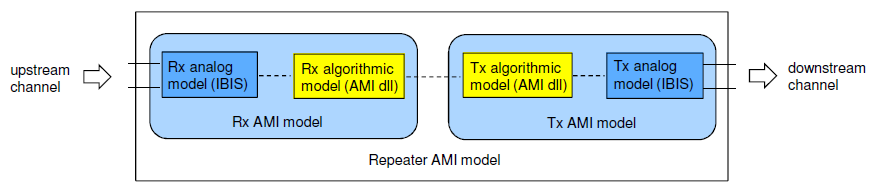
Within a repeater, Rx sits at the front to receive signals from upstream, then pass to Tx part of the repeater to transmit again toward the downstream. So one really can’t work without the other. Plus also “paired” Tx AMI at upstream and final Rx AMI at the end of the downstream, it takes at least four AMI models in most cases to start the analysis. More than one repeaters are also allowed so the number of “paired” AMIs can grow. The proper analysis sequence when repeater(s) is involved is also documented in 10.7 of the spec.
So far as repeater being an “electrical” component is concerned, there may be no such needs to probe signals between Rx and Tx within a repeater. However, when we model an optical link as a repeater (shown below from Agilent slides), then thing becomes much more interesting:
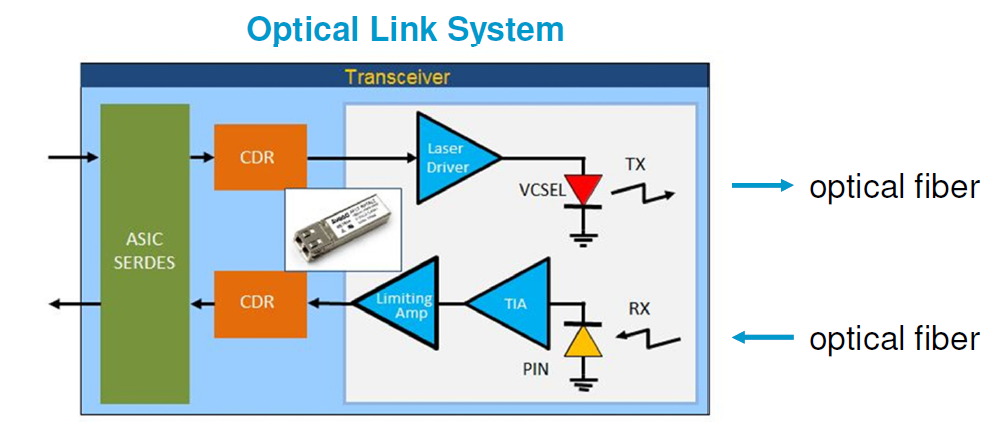
We handled such a case just recently… an optical transceiver used in an (electrical) system may be modeled as a repeater. Having that said, please note that in “optical” world, Tx is now again at the front of the repeater as laser is used to light the optical fiber to transmit signal toward Rx (now the 2nd part of the repeater). So a potential confusion may happen here when optical and electrical worlds meet. In addition, there might be two other considerations:
The first one above is tricky to solve… mainly due to the non-differential nature of signals in a link simulator. Until now, if one reads the AMI portion of the IBIS spec, he/she should notice that the signal mentioned are always differential. So while there is no problem to create an AMI model handling single ended signals, how the probing/analysis goes really depends on simulator being used. Having that said, with DDR adopting AMI methodology, the single-ended signal support should happen very soon.
To accommodate needs of different possible users of our clients, we make use of the “pass-through” dummy model again and proposed the following different AMI models combinations:
In usage scenario 1: The modeled Tx and Rx optical ends (each have their own circuitry) are assembled accordingly. Thus if a simulator can handle “single-ended-like” optical signal in between, then this model can be used directly.
In usage scenario 2: The signal between optical ends within a redriver is not of concern and the support of single-ended-like signal is uncertain. In this case, we “lumped” the TxRx together and put it at the front of the redriver. The second half of the redriver is a simple pass-through. As input and output from the first part are always differential, it will meet the expectation of the simulation flow documented in the spec.
In usage scenario 3: we assume the user is only interested in the downstream end and have only Rx AMI model. In such a case, a repeater will not work because it’s lack of the up-stream. So we combined the created TxRx here and make it a transmitter AMI.
In usage scenario 4: we assume the user is only interested in the upstream portion and only have Tx model. Similar to scenario 3, we combine the TxRx of the optical models and make it a receiver AMI.
In the “paring-off” for a repeater, there are two points worth mentioning:
When we focus on more technically challenging AMI models, we often forgot still important role a traditional IBIS model will play in link analysis. Simply put, the accuracy of an IBIS model still impacts the final results (e.g. BER eye) greatly.
The normal process of the link analysis starts with “link characterization”. Mostly this involves a time domain simulation of driver driving through interconnect with receiver analog front-end (no EQ) connected to obtain the pad to pad step response. Then this step response is differentiated to obtain the impulse response. Finally AMI models are brought into play by convolving with impulse response (LTI or statistics mode) or processing with bit response sequence (NLTV or bit-by-bit mode). In this characterization stage, no EQ (i.e. no AMI) is involved. It’s is their “analog front-end”, i,.e. IBIS models or corresponding spice/behavioral models being used. Thus, the accurate modeling of this portion does impact the processed link analysis results.
In the picture above, eye plots of identical AMI model yet each with different IBIS models are shown. It’ clearly seen how IBIS’s VT waveform and IV curves affect the eye openings width and height. Thus the third scenarios we want to emphasis of IBIS/AMI “paring-off” is the AMI model and their corresponding IBIS model.
SPISim is a relative small EDA/consulting company comparing to others such as Agilent, Cadence or Mathsoft (matlab). These companies each have their own AMI modeling solutions and cost much much higher when comparing to our offerings. However, when we look into their AMI product details, it’s not easy for us to find (or maybe even not there?) how the IBIS portion will be handled. As an AMI model is mostly used for SERDES application, differential or current-mode-logic (CML) design is often involved. If one reads chapter 4 of IBIS cookbook carefully (available at the IBIS website), he/she should find that the process of differential IBIS modeling is more complicated than the simple single-ended IBIS buffer. Thus when considering the importance of “paring” between AMI and IBIS, one should really take this into account. An AMI model without proper analog front end will definitely come back to haunt you during validation stage. Interested reader regarding differential IBIS modeling may also refer to our previous post or our 2016 Asian IBIS summit paper.
Preface:
This blog post is written in preparation for the upcoming IBIS summits at EPEPS (San Jose, Oct/18/2017), Shanghai (Nov/13/2017) and Taipei (Nov/15/2017), where I will present paper of the same topic. Slides, example models and audio recording will be made available below:
Motivation:
Many years ago when I entered the signal integrity field, we analyzed the channel by performing spice-like simulation for several hundred nano-seconds at most. Post-process were then done to get FOM metrics. At that time, the bus speed was barely around 1Gbps. These days, high speed-IO SERDEs are common among various computing devices and their speed reaches multi-Gbs or higher easily. Not to mention the several new 802.3 network protocols which have even higher speed (50G~ >100GB). With such high data rate, one needs to “simulate” number of bits at 1E12 level to reach certain bit-error-rate (BER, say 1E-12) with certain confidence level (CI, say 99%) . As such, traditional SI analysis method is no longer valid because it is simply inpossible to simulate so many bits in reasonable time using spice-based simulator. A new channel analysis methodology, like link analysis, is thus needed and invented around year 2003 to address this problem (e.g. StatEye). For link analysis, traditional buffer models such as IBIS are not much useful as they mostly time-domain based. Algorithmic modeling interface (AMI, a subset of IBIS) models are used mostly instead.
AMI modeling is very technically challenging, it requires cross domain expertise such as simulation, modeling and C/C++ programming across different OSes and platforms. Thus it usually takes much longer for an engineer to ramp up to be able to develop and deliver a model when comparing to traditional IBIS. Two of the big hurdles which cause this slow ramp-up for AMI modeling are the requirements to express the circuit’s behaviors in C/C++ language and then be compiled according to Spec’s API requirements. To lower such barriers, we are asked often: 1. Can we create an AMI model using scripting languages? 2. Can I simulate existing spice models using link simulator before committing to develop a full blown C/C++ version?
We propose approaches to meet these two common requests in this presentation.
Background:
Channel analysis: Nowadays the high speed link analysis most definitely includes stages such as Tx/Rx EQ, which are beyond traditional IBIS. Equalization is needed to compensate channel noise such as inter-symbol interference (self-channel interference) and crosstalk (co-channel interference). These EQ stages can open “eye” from a closed one of a noisy channel, represented by S-parameter interconnect.
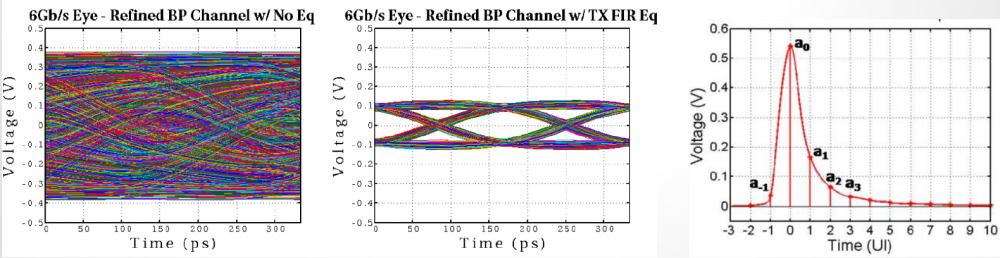
There are two analysis methodologies for modern link analysis:
AMI models support both of these two channel analysis methodologies.
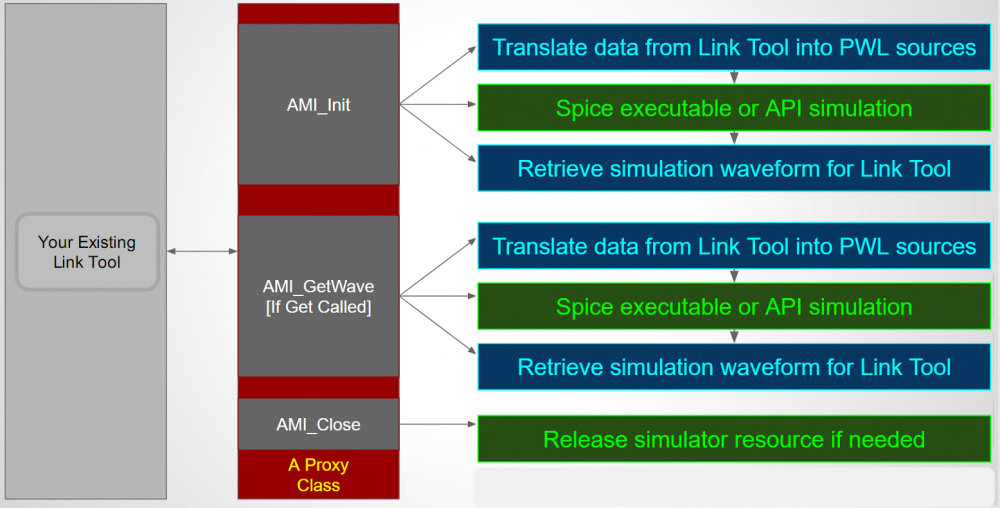
AMI Model: an IBIS-AMI model contains several parts:
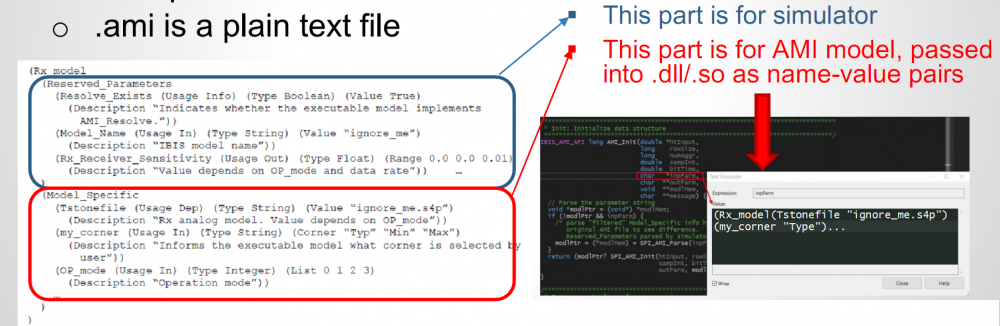
AMI-API functions: As of IBIS Spec. V6.1, there are up to five API functions can be used in a compiled AMI model:

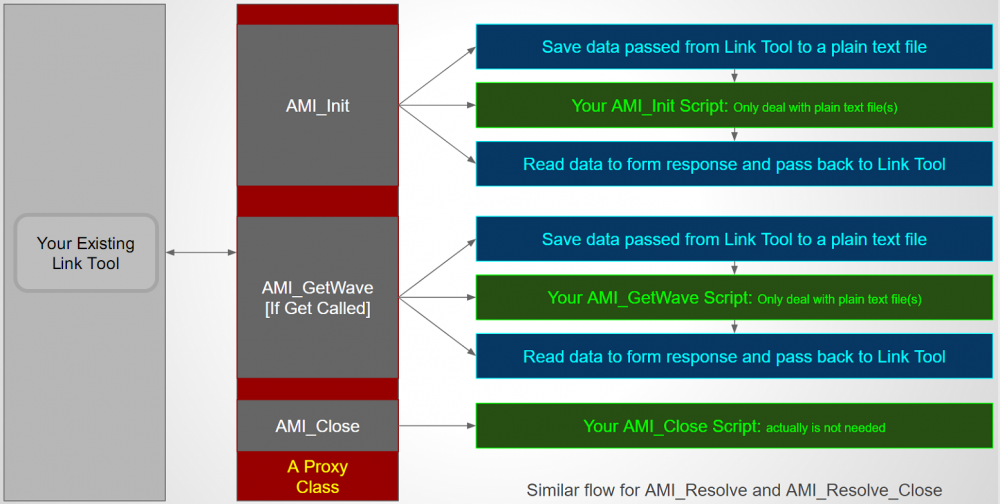
Among which, AMI_Resolve and AMI_Resolve_Close are for string parameter pre-processing which can be ingored in a lot of cases. AMI_Close is like garbage collection/clean-up to release allocated memory, so is trivial is most cases as well. Modern OS may reclaim memory space back even one does not do any “Free” or “Delete” there in AMI_Close. Two most important ones, AMI_Init and AMI_GetWave, are marked in red. In particular, they participate in the aforementioned “Statistical (for LTI)” and “Time-domain bit-by-bit (for NLTV)” models. That is, for a LTI model, its AMI model must/should implement the AMI_Init function call. A LTI model can also implement AMI_GetWave function call but this is optional. On the other hand, a NLTV model must implement AMI_GetWave function while implementing AMI_Init as “initialization” rather than “computing” portion of the codes. The bit-by-bit convolution part of a NLTV model should be implemented in the AMI_GetWave part of the codes.
When looking at the function declaration part of the spec, as boxed in red in right part of the image above, one should also realized that the first arguments (an array represented by double pointer) serves as both input and output purpose. These are “pass by reference” arguments as they are pointer. So at the beginning of the AMI_Init/AMI_GetWave calls, the model can obtain either impulse response of the channel or digital bit sequence from the simulator via this pointer. Then the model perform necessary computing using info from the rest of the arguments (some of them also serve as output purpose, such as char **msg, but is not that important in this context). At the end of the computation of this function call, the modified response must be filled in back to the address where the first arguments points to, so that the link simulator will retrieve the values and carry on the rest of the analysis.
AMI Modeling Flow:
A typical AMI modeling flow involves the following steps:
Now let’s talk more about item 2 above. There are many considerations on how you should code this part. A specifically C/C++ coded model for one circuit will mostly run very fast. However, it may requires frequent re-compilation/re-testing when new design comes. If we can make this part as simple as possible and non design specific, such as calling external scripts, then this work may only need to be done once as all the variation are now external to the compiled .dll/.so.
Modeling with Scripts:
Knowing the requirements of the AMI API, we can now propose a flow to create an AMI model using user’s favorite scripting language:
Flow:
To support script based AMI modeling, we need to have a thin API implementation (in C, as required by AMI Spec) whose sole task is to translate all the received arguments into a text format and write as a text file. It will then pass the path of the text file to user defined scripts or batch file via system call. Location and type of the script is defined in advance in plain-text .ami file. The script needs to retrieve the argument information first by parsing the plain text file, perform necessary computing, then write into another or same text file which this AMI model with thin layer knows where to find. So when the script completes, the AMI model will parse the text file generated by the script, fill the information back to the aforementioned “passed by reference” pointer array, then complete this step. As discussed, whether the scripts is needed for either AMI_Init or AMI_GetWvae or both are pre-defined based on circuit behavior. And since this is developer chosen favorite language, parsing and writing to text file should not be an issue when comparing to say C language. Lastly, should there be any information need to be passed between API calls (such as model member’s values between AMI_Init and AMI_GetWave), they can also be file based. To summarize, the AMI model with thin layer completes the API calls with upper simulator like other regular AMI models. However, its “transactions” with underlying user’s scripts are all file based.
Example:

A matlab example of the AMI_Init is shown above. In the matlab codes, it first calles parseInput function, which is a text file prepared by the thin AMI model and contains input waveform. It then performs computation such as convolve with FFE, then the result matrix is written back to the text file via storeOutput function call which thin AMI model know where to find. Since matlab’s “conv” function is used directly, the model developer does not need to deal with c-based implementation details such as memory allocation FFT/iFFT in some cases or other math library linking/compilation.
Considerations:
While script based AMI development is simple and handy, there are several considerations before deciding to release such models:
Modeling with Spice circuits:
Now that we know a thin layer can call external script either directly or via its interpreter, we may also come to the conclusion that it can also call external program such as a circuit simulator. This is of course true!.
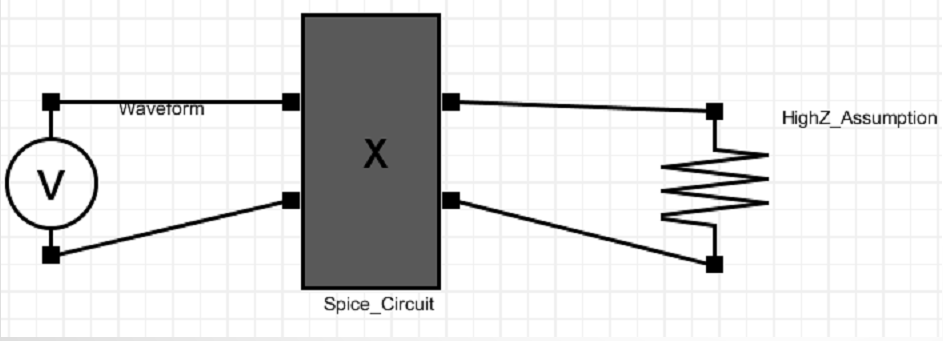
An assumption we mentioned at the beginning of the post is the “High-Z” condition. In a typical spice-like nodal analysis, there are many “Newton-Raphson” iteration going on within same time step. At the beginning of each Newton iteration, tentative voltages are given at each node. Each components then compute the drawing or output current into these nodes based on these voltages and its own behaviors. At the end of the iteration, circuit simulator solves the system matrix to see whether KCL/KVL reaches balance and then determine either another Newton iteration is needed or it can march into next time step.
In channel simulation, such iteration is not needed as there is a “High-Z” assumption… and that’s why it can run much faster than nodal spice simulation. In High-Z assumption, each blocks is assume to have high input impedance and output impedance so it will not draw any current at the input and the output is set once determined. Since the thin layer AMI model can obtain the inputs from simulator via API call, if it can perform another task… such as convert this inputs input PWL source with time step equal to UI/number_sample_per_UI (both are know and passed by the simulator), then it can theoretically call a simulator to drive user provided spice subckt like above. Note that the input waveform is just voltage which represents potential difference of two nodes. So there is no reference to GND at all. It’s subject to user’s spice circuit to determine what the reference is and provide GND reference if needed.
Flow:
The picture above shows the flow to simulate/model AMI with spice subcircuit. It is very similar to the flow for AMi with scripting language. First the thin layer AMI model need to generate a PWL source dynamically based on the provided inputs. Then form (either write out as a file or internally in memory) a netlist as a driving circuit and probe at the output. This driving circuit will use user provided spice subckt with possible value overrides defined at the .ami file. Then thin layer AMI will call external spice simulator (or internal API) to perform nodal based simulation. The output (like .tr0 for HSpice) is then processed and its value is again filled back to the initial API pointer array to return back to upper circuit simulator.
Example:
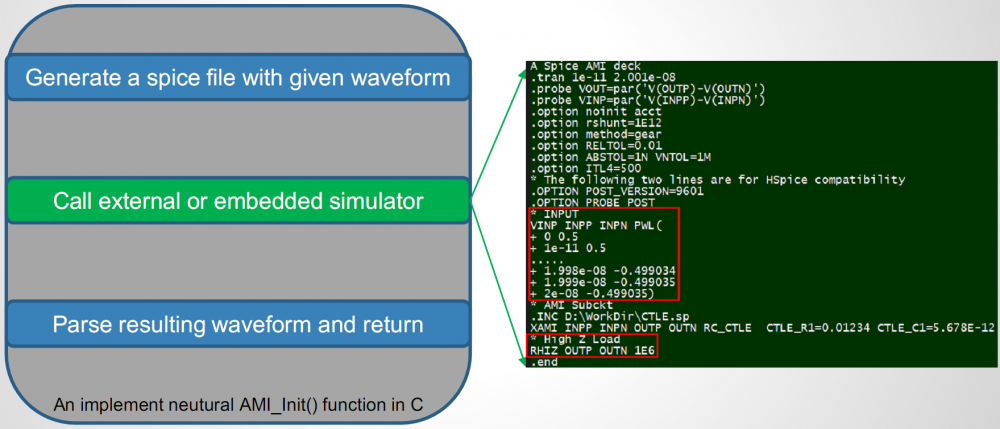
An example is shown above. The template is pre-defined with the PWL source and path to user’s spice circuit being left to be filled-in. The thin AMI generates the netlist with all values filled properly upon being called by simulator. It then call external simulator to do nodal simulation. Resulting waveform are post-processed and filled-in to the API argument memory address and complete this API call.
Considerations:
Similar to the AMI modeling with script language case, there are several considerations when adopting the spice-based AMI modeling approach. First is the performance… as each AMI API call involves nodal simulator initialization (allocate matrix, solve for DC, Newton iteration between each time sample etc), it will be significantly slower than pure C implementation. However, this is less of a concern if only AMI_Init is needed as it’s called only once. More over, one does not need derive any equation or do any coding at all and can get accurate link performance using this Tx/Rx circuitry directly… so development time is saved significantly there. If one decides to implement such block in C/C++, then simulation results obtained during this process can serve as a very good reference or correlation data for C/C++ based model to be developed.
Another consideration is again the distribuability: If this spice model has particular MOSFET model and requires say HSpice, then the AMI model recipient also needs to have HSpice in their environment in order to run. While commercial simulator like HSpice may not provide API or serve as shared library, many open source ones do. Examples are NgSpice and/or QUCS. In these case, the compiled thin AMI model is basically a simulator in .dll/.so form and can perform simulation all by itself. The binary size is around 8MB larger then without as it also needs to link with all simulator supported device models as well.
Summary:
Using either scripts or existing spice circuits for AMI modeling is actually doable. The presentation I give here is not just talk on paper. The implemented “thin-layer AMI” and examples are also provided together with the slides. These flows can be considered as part of the AMI development process as they can shorten the modeling cycle significantly while providing data for correlation should one decide to go full C/C++ implementation at the later stage. The consideration points includes performance, elegance of released models and distributability of either the script’s interpreter or simulator. Also a thin layer AMI models is needed. This thin layer API is called Proxy model in computing science terms. As a matter of fact, SPISim has implemented such proxy models and made them available for public to use free of charge. [Link Here] Having that said, this API model only needs to be done once as all the model variation are located externally in user scripts/spice models. and thus require no re-compilation when design changes. Nevertheless, these two possible modeling approaches provide an AMI model developer alternative ways to decide on how a model can be developed more efficiently and effectively.
IBIS-AMI modeling is a task usually executed at the end of IP development process. That is, hardward IPs are created first, then associated AMI models are developed and released to be accompany with this hardware IP since the IPs vendor usually does not want to expose the design details to the their customers. On the other hand, it is also likely the case that a user may have received behavioral or encrypted spice models first, or even obtain measurement data from the lab, then would like to create corresponding AMI models for channel analysis. Such needs arise usually because either original IP vendor does not have AMI model or may charge too much. It is also possible that end user would like to explore different design parameters before determining which IP/part to use.
In this post, we would like to discuss how such an usage demands can be accomplished with SPISim’s AMI flow without any C/C++ coding or compilation for AMI. Here are the topics for this case study:
Collateral:
For this design, we received a testbench for a typical SERDES channel using this IP. The schematic is shown below:
Both Tx and Rx are encrypted hspice models with adjustable parameters. When picking one set of parameters to test run the channel test bench, we get valid simulation results.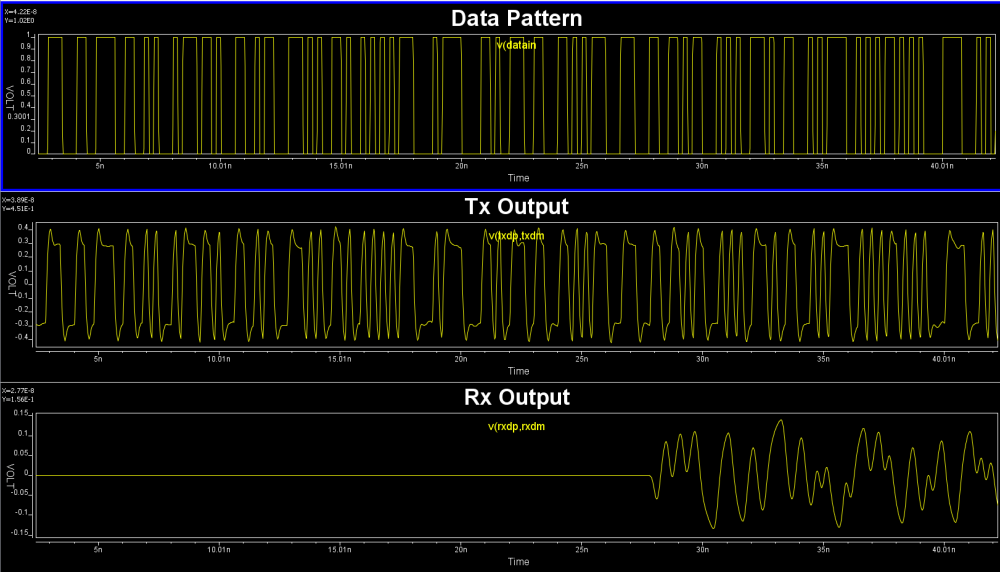
As this is a hspice netlist, we have the freedom to probe different points and change the simulation options as needed (for example, from transient to ac or transfer-function).
Design Spec. and modeling goals:
The original IP vendor only provides simple descriptions for various blocks and design parameters. The Tx and Rx packages are spice sub-circuits and channel is a s-parameter file. Both Tx and Rx model has typ/min/max corners. On the Tx side, there are settings for voltage supply which is independent with the corner settings, a 7-bit resolutions for a multiplier to work with the swing amplitude, a 6-bit resolution for a de-emphasis and a flag for turning-on/off the boost.
With these IP design spec, the modeling goal is to create associate AMI models which will allow end users to fine tune performance with similar parameters like original IP. Further more, SPIPro is used for its spec. AMI model so that model developer should not need to write any C/C++ codes or perform any .dll/.so compilation for this AMI modeling.
Modeling process:
If one needs to create AMI models from simulation or measurement results, that usually means he/she does not have original design details or even design spec. available. So the so called “top-down” approach will not work simply because there is no design at all to translate to corresponding C/C++ code. Instead, we need to create an architecture via trial-and-error to “reverse engineer” the design so that the performance will match what’s given. Here are the steps we used in this case:
While the full channel test bench demonstrate how the Tx/Rx work, it also includes information not needed in the AMI modeling. For example, package and channel are usually separated from the AMI model because they are usage or client specific. Besides, as mentioned in previous posts, one assumption of AMI model is high-Z input and output. So the first step of the modeling is to separate channel from driver/receiver and create Tx and Rx only test bench together with inputs and outputs.
For Tx, it’s a simple PRBS input with output connecting to 50 ohms loads.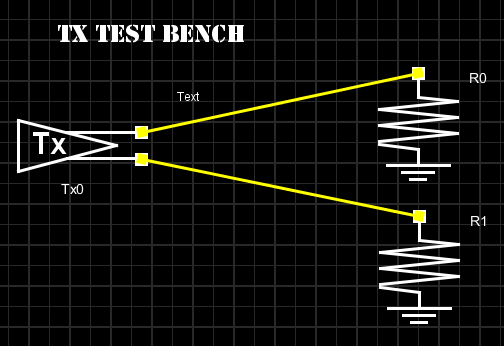
And its input/output should look like this:
When we modify the test bench to connect Tx directly to Rx, i.e. bypass all the package and channel models, we get such input/output eyes:
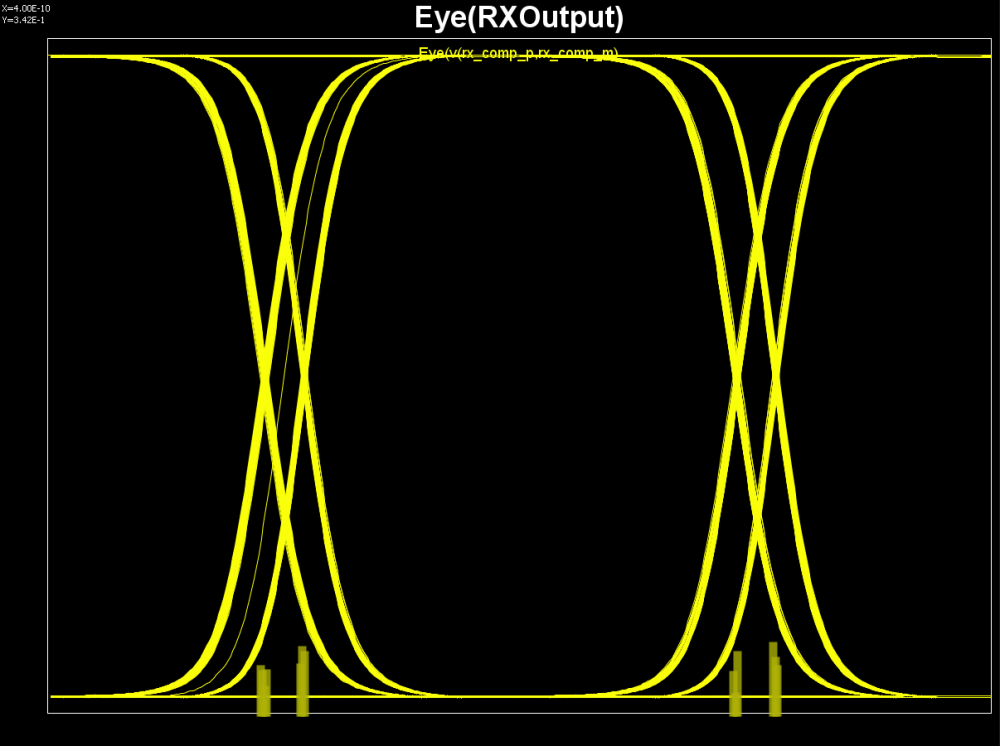
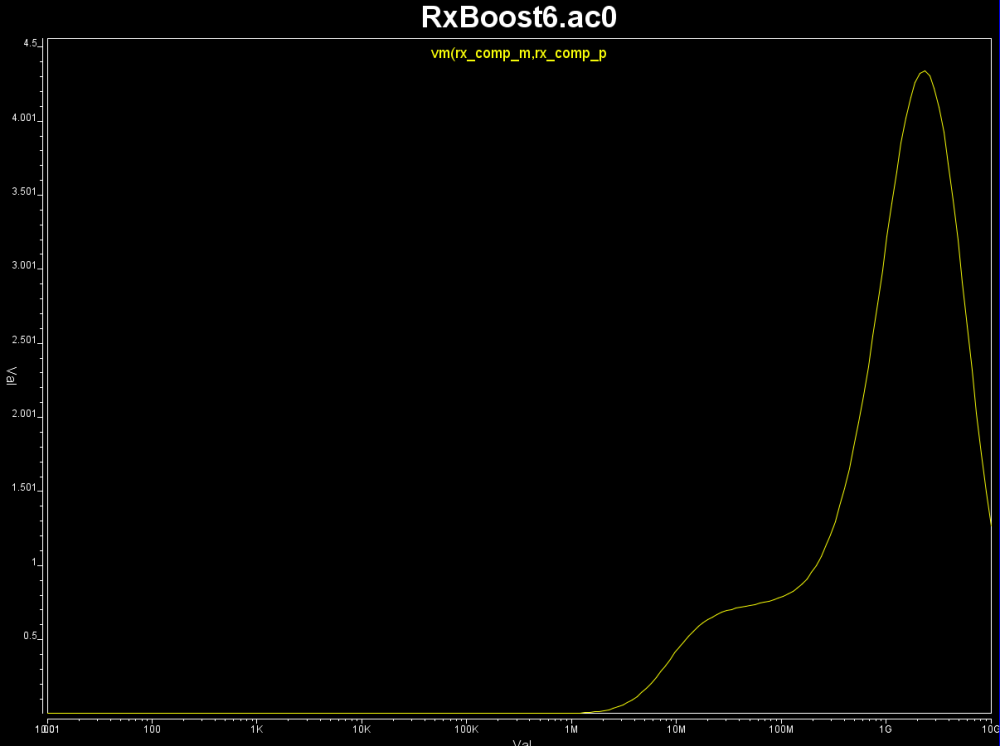
From these eye plot, we do not see DFE like abrupt force-zero output, thus the Rx model seems to be a CTLE like boost filter. So we created Rx test bench like below and obtain its frequency response:
Note that in order to perform what-if analysis of next step, we also use VPro to capture inputs to these Tx and Rx models so that they are evenly spaced.. as required by AMI’s Init and GetWave function. These evenly spaced inputs will be used later on by SPISimAMI.exe to drive the model. For HSpice, the following option may be needed so that the .tr0 file will have evenly spaced data points even simulation is various time-step sized:
Now that we have input data and desired output for this particular set of parameters, next step is to explore whether SPISim’s existing spec. model is sufficient to meet the performance.
Tx: for tx module, we observed the following two characteristics:
For the de-emphasis part. We can use Spec. AMI’s what-if analysis to see how different pre/de-emphasis settings will cause difference responses:
We change these pre and post cursors one at a time only, using -0.1 for value .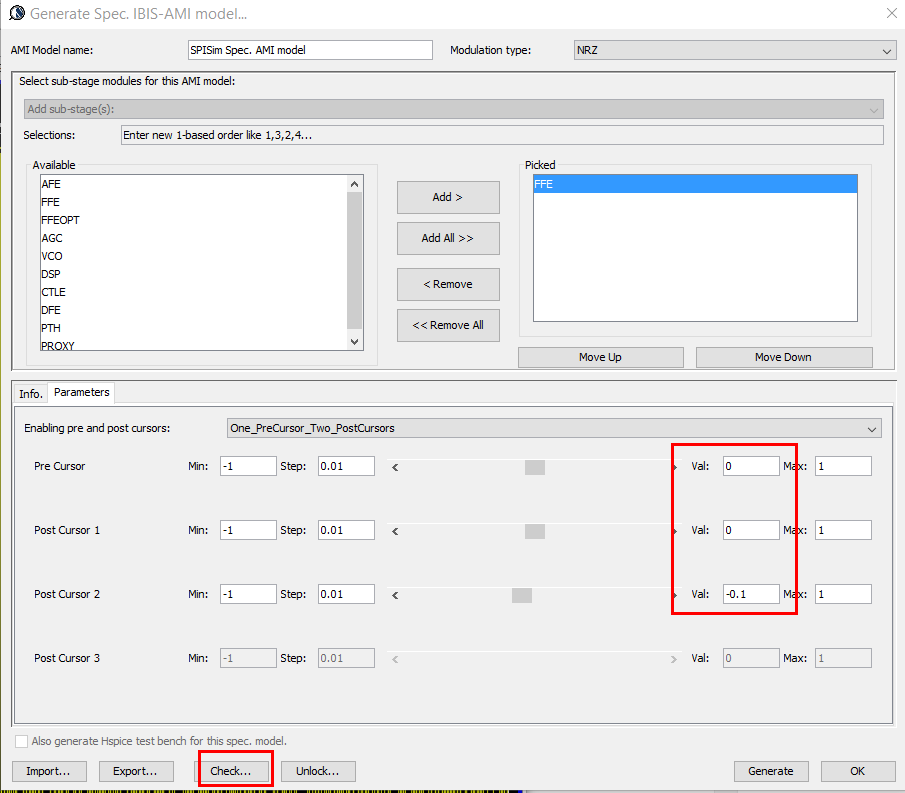
We then test drive using built-in PRBS with same UI time, 200ps:
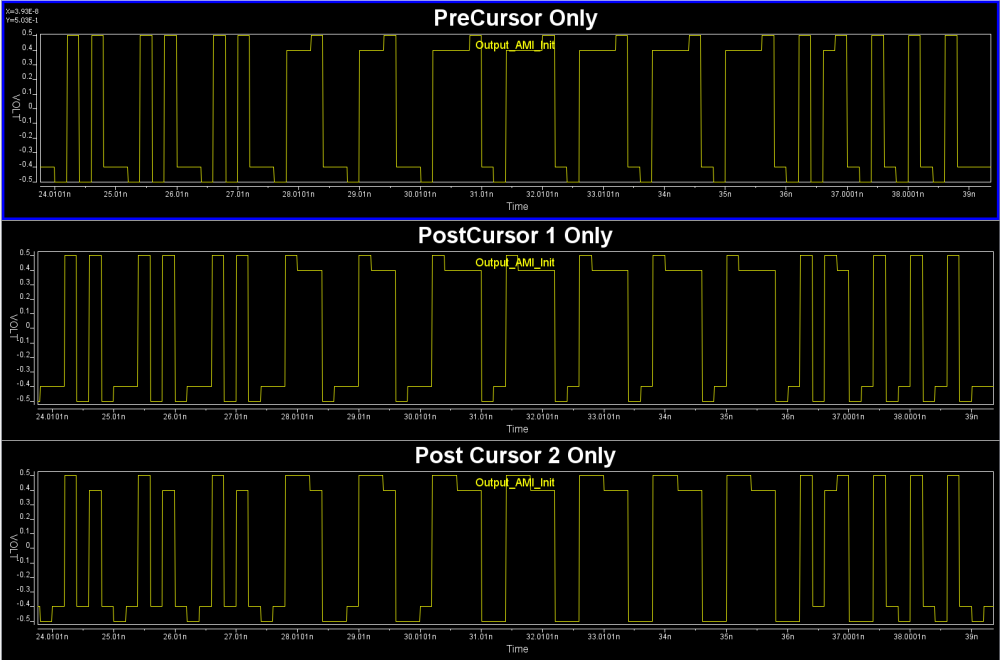
From the summary plot above, and correlate with the Tx output, it’s apparently that this Tx has one post-cursor FFE beause only this set-up gives de-emphasis after one UI after the peak.
For the output swing and slew rate, it’s the sign of AFE (analog front-end). So we can simply add an AFE stage right after FFE, with high/low rail voltage “clamped” to the simulated peaks:
With several trial-and-errors, all within SPISim’s Spec-AMI GUI, we obtained the following Tx correlation between spice test bench and AMI results for this particular set of parameters: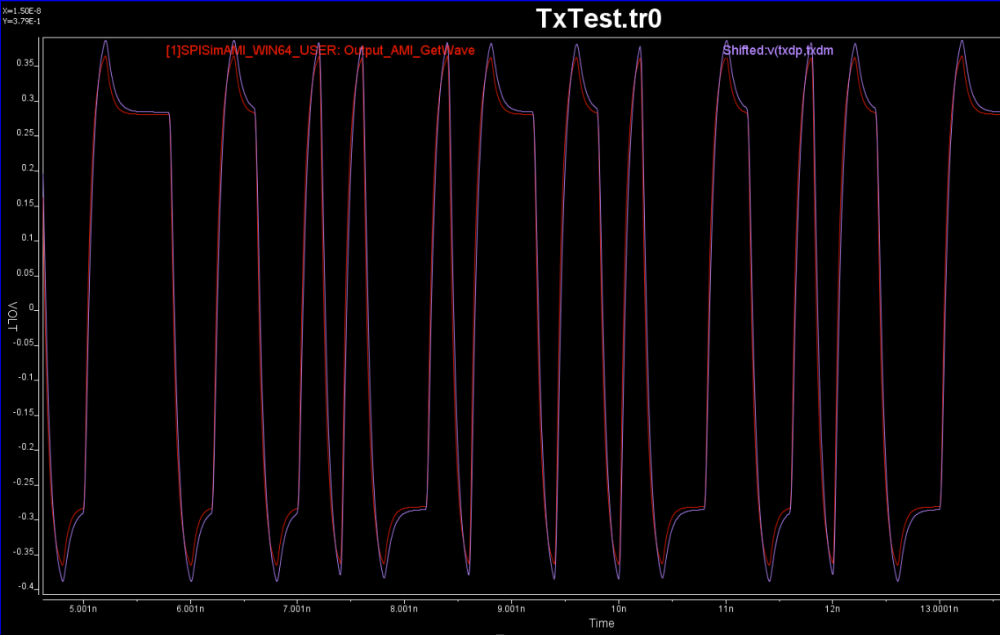
Similarly, as Rx behaves like a continuous filter, we use a CTLE stage to mimic its behavior: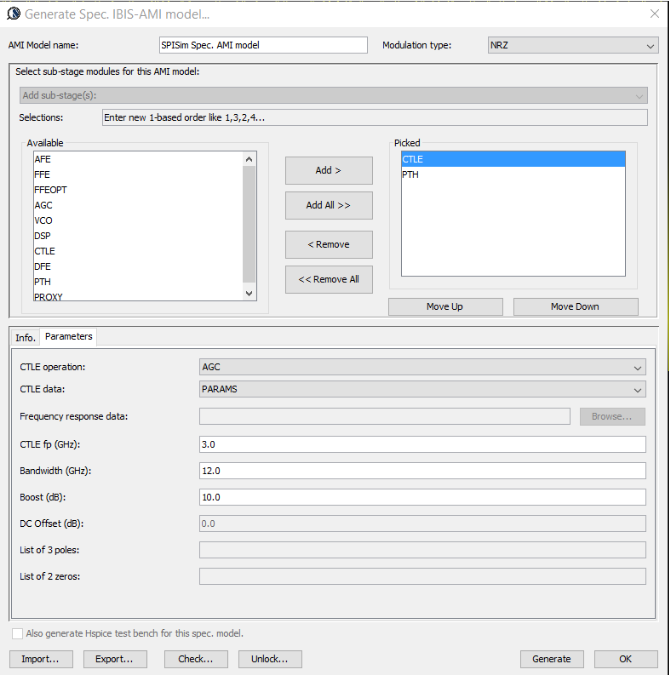
With several tuning, we obtain such Rx correlations: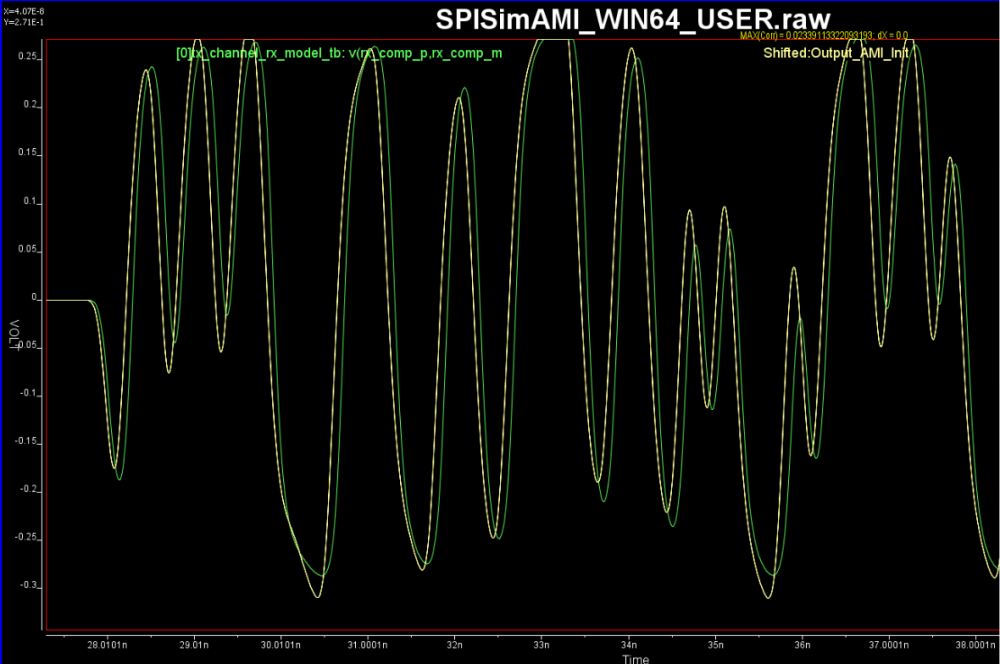
From these correlations, we believe that the stages built-in to the SPISim’s AMI are sufficient to meet the performance needs. So next step is to find the parameters to support all these design specs.
As similar process between Tx and Rx, we will use Tx as an example to demonstrate the flow.
Before generating a simulation plan, we first also make sure these design parameters are independent with each other. We performed simple 1D sweep (several points) in particular for the swing and de-emphasis level.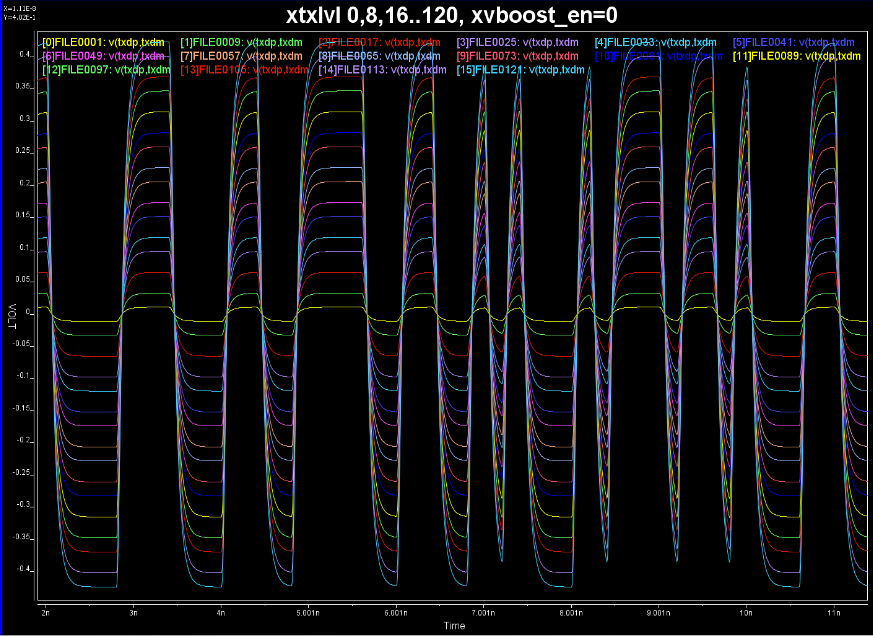

Notice that the slew rate and peaks are not affected by de-emphasis level much. In addition, the spacing seems linearly spaced according to the bit settings. With this, we can sweep them independently.
Now for Tx, a full factorial sweep will require 2^6 (de-emphasis level) * 2^7 (swing level) * 2 (boost flag) * 3 (corner) * 3 (voltage levels) ~= 150000 runs. Due to the linearity, we do no need to sweep full 6 and 7-bits of de-emphasis and swing levels. Instead, we increase step interval for simulation because SPISim’s model’s built-in interpolation can be applied automatically, more about this at the model release section.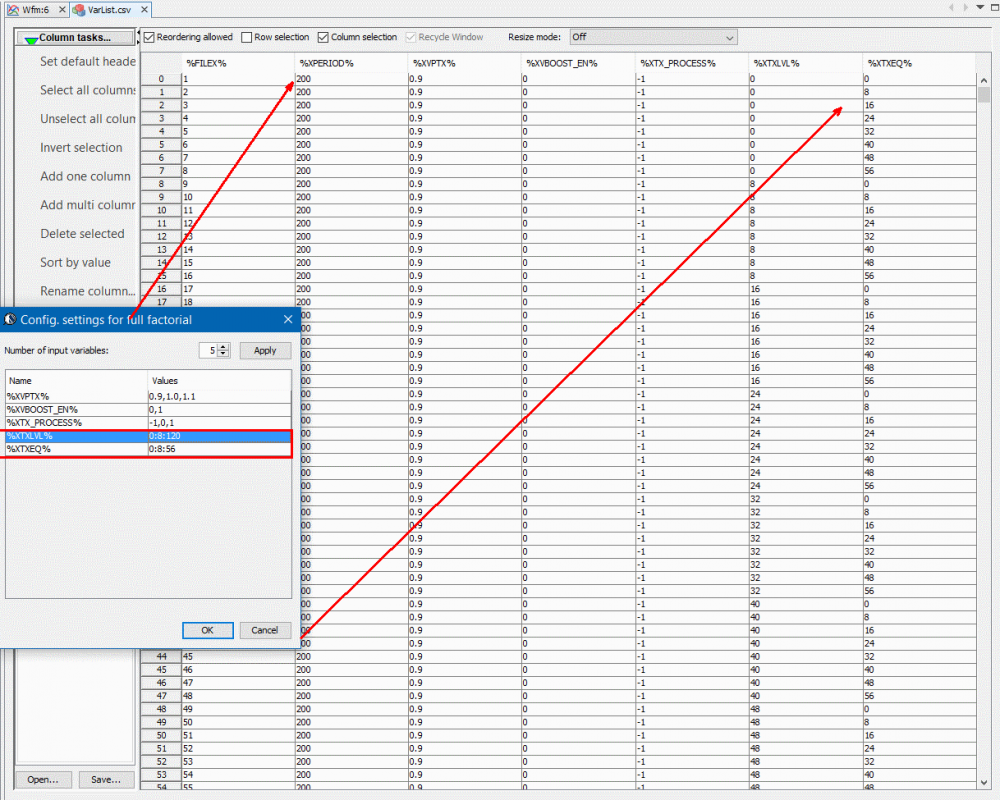
For these five variables, we use MPro to generate 2403 test case (1/60 of full factorial). We then create a template from the Tx spice test bench so that parameters can be updated according to the table and its column header above:
Noticed that variables are enclosed with “%” (e.g. %XVPTX%). Their values are replaced by corresponding values in each row of the table to generate a new spice file. With all these 2403 spice file generated, each for different combinations of parameters, we kicked-off the batch mode simulation and obtained all two thousand cases within one hour. This is done all within MPro and can also be done using user’s script.
With all results being available, next step is to find corresponding AMI parameters for each of the case. SPISim’s model driver, SPISimAMI.exe, is a must have here. It will take the collected, evenly spaced inputs to drive the AMI parameters together with the SPISim’s spec. model, output results can then be correlated with the .tr0 file simulated with HSPice for that particular case. In case when the correlation is not good, AMI parameters should be updated again for another iteration of performance matching. This process is summarized in the flow below:

Apparently, such as task is too tedious and error prune for a human to perform. Since the input pattern is the same, relative timing locations of different properties (such as peak and de-emphasis levels) are also the same even between different test cases, we can process these data automatically. Regarding “adjusting” AMI parameters, a simple bi-section search will quickly converge to the desired de-emphasis tap values for the given test case.
In our process, we first parameterized the .ami file as shown below. This ami file is based on the architecture identified in the second step… only that now we need to find different values for different parameters. In particular, the swing level and FFE post tap are unknowns and need to be swept.
Because these two variables are independent, we can first identify the peak value as “Swing” from the .tr0 simulation results, then use bi-section to adjust the FFE_PARM_POS1 such that the output from SPISimAMI for this .ami file settings and SPISim’s spec .dll/.so will match the tr0 data.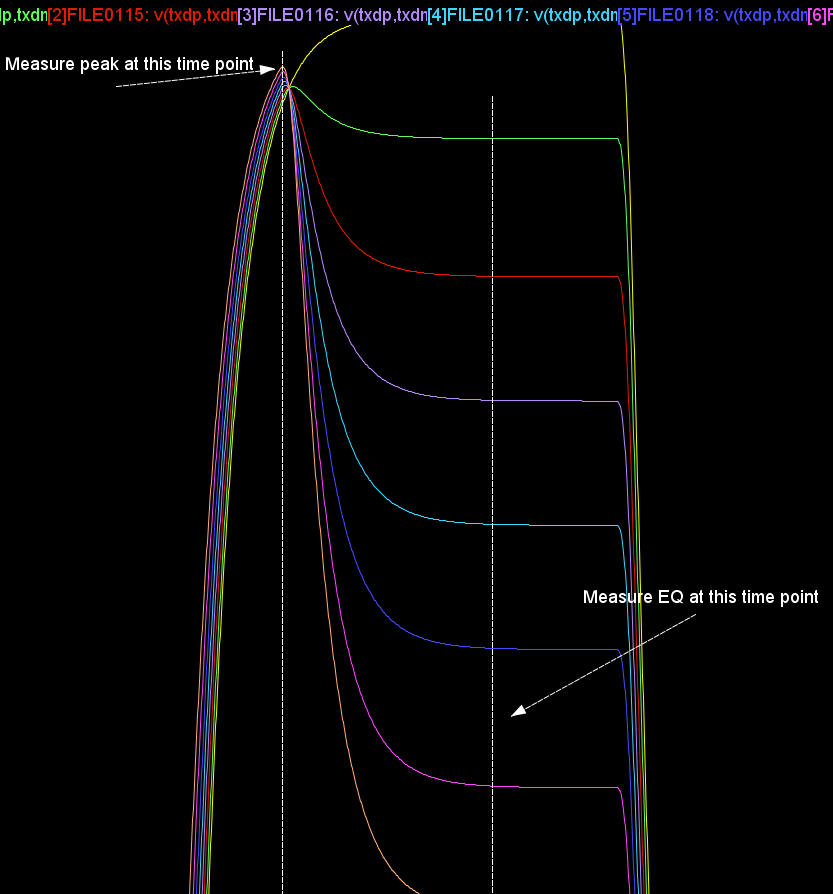
With this flow and process, we use our SPIProcPro to bath process the simulation results and get all 2403 fine-tuned AMI parameters within one hour:
Here is the partial config. settings for SPIProcPro of this modeling process: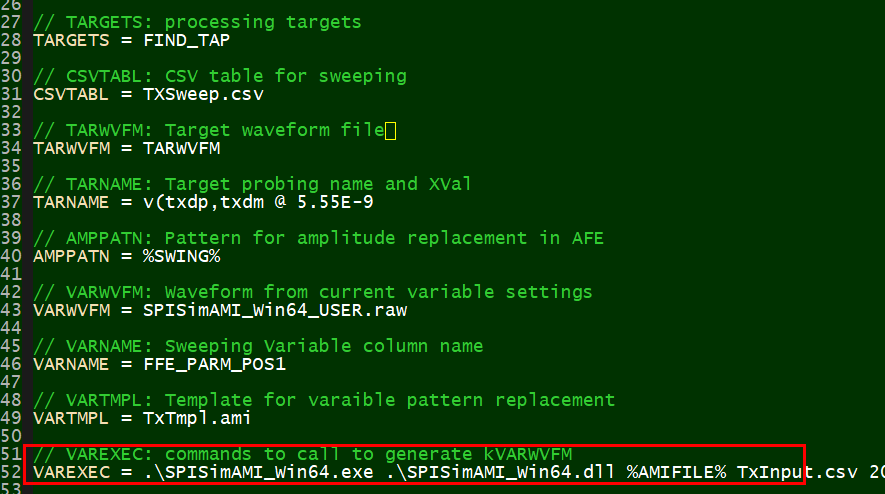
For each of the test cases, the post-processed AMI result is saved to an individual .csv file. All these csv files are also combined and then concatenated side-by-side with original input condition. The end result is a table with input condition at the left and associated AMI parameters at the right. This table will serve as pre-set data table for our AMI models to be released.
Model release:
The combined table looks like below: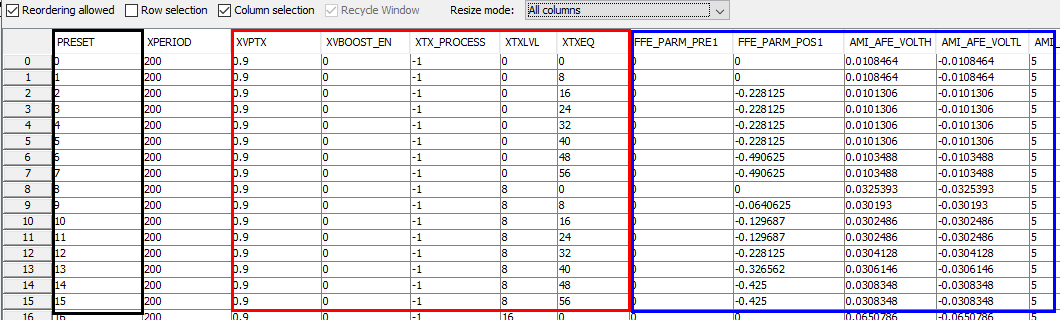
The columns boxed in blue above are those required for SPISim’s AMI spec models. These columns has header named exactly the same as those in the ami file green boxed below. The row entries for settings of each test case in the csv table is filled in to the boxed in red in ami file below.
Now this is not the format to be released to the AMI user. In stead, the design parameter we want to expose to the end user are listed in the red box in the csv table. They have the column headers matching original IP’s design parameters. Also note that this csv table only contains partial results as we didn’t perform full factorial sweep for all ~150000 cases.
The design parameters, boxed in red in csv file, need to be able to be mapped to those boxed in blue, the AMI stage’s parameters.
One unique feature of SPISim’s AMI model is it supports of table look up and up to two dimensional linear interpolation for numerical values not found. The set-up is easily done from model config. GUI. The example below is for PCIe with 11 preset tables.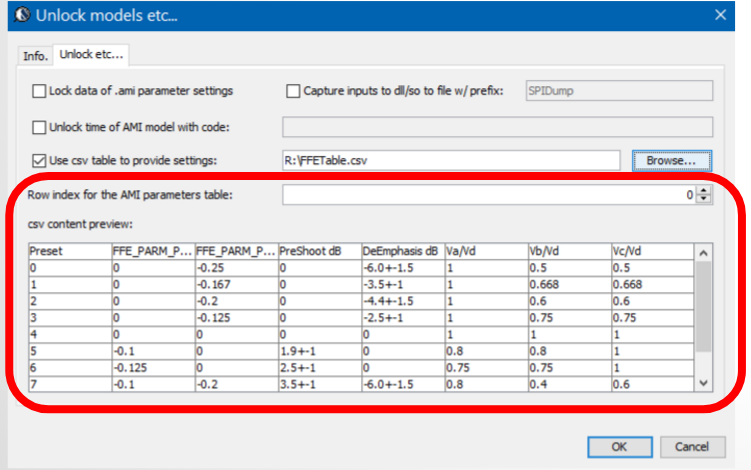
In this case, we do not use preset index. Instead, we set the preset index value to “-1” to signify that model’s table look-up will be used: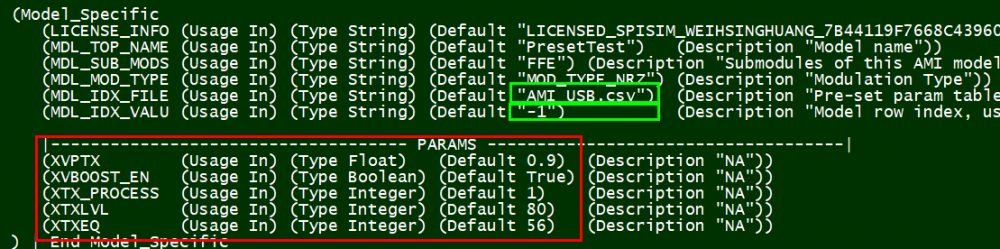
In the final .ami file above, the exposed parameters (boxed in red) are exactly those defined in the original given IP. Their name and values will be used to look-up from the table to find matching row. If up to two rows have no exact match in terms of numerical value, linear interpolation will be performed by the model during initialization. A final matching row or values will be used to assign to the parameters required by spec model.
The final results of the create model is one .ami file, one .csv file (plain or encrypted), and one set of .dll/.so file. There is no need to write any C/C++ codes or even compilation for the AMI modeling purpose and the SPISim’s spec. models can be used directly. For the post-processing portion, a python/perl/matalb scripts can be used instead if SPIProPro is not sufficient.
Other thoughts:
In this case study, a look-up table based approach is used to create AMI model via reverse engineering. Alternatively, we can create a spice simulation session using our SSolver/ngspice spice engine to simulate these given Tx/Rx spice model directly. The pre-requisite for this approach is that the given hspice model is not encrypted, can be converted to the SSolver/NgSpice based syntax and has no process file involved. Regarding search mechanism, a bi-section searching algorithm is used in our modeling process here as there is only one value (EQ variable) needs to be determined. The amplitude/swing is deterministic and can be found once tr0 simulation results is post-processed. If there are more than one variable involved for optimization , such multi-tap EQs, then a gradient descent based algorithm may be needed if full surface sweep is not practical.
Preface:
It has been often believed that IBIS-AMI modeling imposes a comparably high cost and technical barriers to get started. An AMI modeling engineer certainly has the due diligence to be familiar and understand the basic of link analysis or AMI flow. However, the requirements of implementing the models in C/C++ codes, compiling them into .dll/.so libraries, and being able to run on third party (often expensive) EDA tools with consistent results are often too much to ask for… or at least will increase the design cycle. To meet these challenges, several big EDA companies have provided top-down based flow for AMI generation directly from architecture codes. In exchange with the “click-button” convenience, SERDES needs to be designed in its environment first and tool’s up-front expense also needs to be considered. Further more, the long term cost of the generated AMI models (in terms of model support, maintenance and extensibility) are often ignored. It’s also true that even with these top-down flows, compilation on different platforms (win32, win64, linux) etc are still inevitable.
We published several free tools recently and presented a paper at the recent IBIS summit regarding AMI modeling. Together with other open source/free link analysis tool to be mentioned at the end of this post, we think it’s now a good time to consider an alternative AMI modeling flow. This proposed methodology in this post will be economic (no front end tools cost) and efficient (give SERDES/AMI developer most control).
[Note that in this post, we use link tool/simulator alternatively to represent the application loading IBIS-AMI models and calling their functions.]
Concepts:
Engineers familiar with Spice-like simulator know that we usually only need one platform specific simulator (binary). Schematics netlist is in plain text format and can be used cross different platforms (assuming good practice such as relative modeling path, file line endings are followed). A general purpose spice simulator is not design specific so there is no need to have different simulators for different circuit or IC design. This compatibility is achieved by building on simple rules, i,e KCL and KVL and linear algebra. This way a simulator can decoupled from the implementation details of design specifics.
In the “AMI-modeling” world, are there such simple rules to be found so that we don’t need to compile a binary just because the design is different? Understood that there are always trade-offs: e.g. simulation speed of design specific binary model vs slower yet convenience during modeling cycle, then at least we should find a way so that modeling engineers can focus more on the basic of the algorithmic blocks and hopefully, still find a way in a later stage to generate a speedy model with minimum extra tasks (C/C++,dll etc)
AMI model, at its current scopes, is mainly for SERDES application. They are mostly point-to-point system or can be processed stage by stage. We may also think it this way by looking at the defined AMI-API function prototypes:

AMI_Init and AMI_GetWave are two main processing routines defined in the API spec. Various arguments are passed-in and the AMI models are responsible to perform designed algorithmic within the model then return these values in place. By “in place”, we mean the impulse_matrix’s and wave’s content will be modified in the same memory address before returning back to the calling application… which is mostly simulation platform or circuit simulator.

Based on these observations, we can liberate the couplings between 1) link tool and models, and 2) models and underline algorithmic processing. Via these decoupling, an economic yet efficient flow can be made possible.
Decoupling within the model:
First, we want to observe how data are being passed from the link tool to the model. In the schematic above, the input to the Tx stage is either channel’s response (LTI mode) or bit pattern (NLTV). If the Tx is a simple pass through, then Rx will receive similar information without being affected by Tx:

Take AMI_Init as an example, we can achieve this decoupling using SPISim’s free SPISimProxy model. SPISimProxy will write the argument received from the link tool to a plain text file. After the AMI model’s processing, it will again write out the processed data to another text file before finally giving back to the link tool. This way data being exchanged between link tool and the model are now exposed… even if they both are compiled binaries. The two blue boxes above represent such generated text data. The main function of the AMI_Int function, purple block in the middle and existed in the model’s .dll/.so file as a form of the C function, is to transform input to output response.
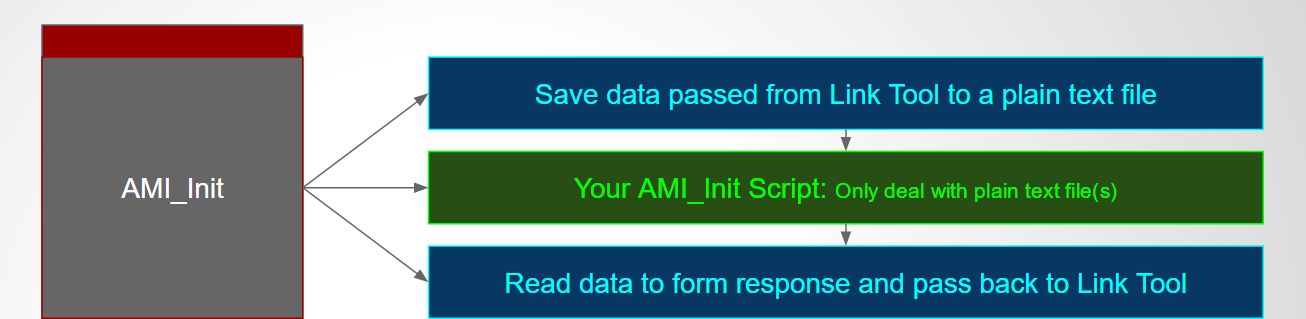
With this, we can now replace the AMI_Init function with our own… we can write this function in matlab, python, perl, java etc language instead of more demanding C/C++ form. It only needs to interface with two text files just exposed with the following operation sequence:
Because each of these steps can be customized by Proxy’s .ami settings, a configuration file or even environment variables, AMI developers are now liberated to use what ever languages they preferred without dealing any C/C++ if they like. There is also no need for .dll/.so compilation as SPISimProxy has been pre-compiled to support most of the platforms.
The example above uses AMI_Init as an example, other API calls, such as AMI_GetWave or AMI_Resolve can be done in similar fashion. Clean-up calls such as AMI_Close or AMI_Resolve_Close are also supported in SPISimProxy model so if needed, AMI modeler can also clean-up all these file traces at the end.
Part of the arguments passed from the simulator is the model pointer. This model pointer (void*) is supposed to be persistent during the AMI process. The script author may use file based persistence mechanism across AMI_Init/AMI_GetWave calls to store constructed data structure or settings etc. By avoiding using C/C++ specific pointers or data structures, the process becomes neutral and can support many different languages.
Decoupling with the EDA tool:
The aforementioned process requires an application to drive the proxy model, and thus the modeling scripts. This can be achieved with our free SPISimAMI.exe. It’s again pre-compiled to support most platforms. Its built-in pulse response enable user to model LTI based AMI process directly. For bit-by-bit based input data, user may use our SPILite or other free simulator such as our SSolver or NGSpice to generate bit sequence, then feed this input in .csv format to the application. SPISimAMI will then take this user’s input, form the proper arguments and send to underlying AMI models… it can be modeling script current under development, or an existing IBIS-AMI models for testing or validation purpose. SPISImAMI can also be used to drive an existing AMI models via SPISimProxy so that user may get insights about this process. In the demo video we posted on SPISimProxy page, a matlab script has been used to demonstrate the AMI_Init process.
Test drive with open-source link tool:
Once the given response work properly with the prototype implemented in modeling scripts, next step is to run them in a link tool for BER like analysis. For this purpose, pyBert may be used as it also load IBIS-AMI models, including our SPISimProxy.
Up to this point, there is no front-end cost involved in the AMI modeling process and a developer only needs to use his/her own favorite language to deal with plain-text input/output. In addition, the debugging and testing of the model prototype can be done with direct command call instead of multi-step GUI operation/invocation. This not only avoid license needed with 3rd party tool, but also ensures an efficient work flow with easily repeated consistent results.
Optimization and model release:
There are several possibilities to release the models from on this process:
The modeling flow suggested above is not proprietary and can also be implemented within the corporation or the modeling team. We believe that with the liberation of the modeling engineers from these unrelated AMI modeling process, they will be able to focus more on the core business logic, i.e. the algorithmic part and deliver the best quality model for the industry’s progress. Those non directly related tasks can be left for other EDA professionals (* cough *) if needed.