Note:
- Dataset and ipython notebook of this post is available at SPISim’s github page: [HERE]
- This notebook may be better rendered by nbviewer and can be viewed [HERE].


Continuous time linear equalizer, or CTLE for short, is a commonly used in modern communication channel. In a system where lossy channels are present, a CTLE can often recover signal quality for receiver or down stream continuous signaling. There have been many articles online discussing how a CTLE works theoretically. More thorough technical details are certainly also available in college/graduate level communication/IC design text book. In this blog post, I would like to focus more on its IBIS-AMI modeling aspect from a practical point of view. While not all secret sauce will be revealed here:-), hopefully the points mentioned here will give reader a good staring point in implementing or determining their CTLE/AMI modeling methodologies.
[Credit:] Some of the pictures used in this post are from Professor Sam Palermo’s course webpage linked below. He was also my colleague at Intel previously. (not knowing each other though..)
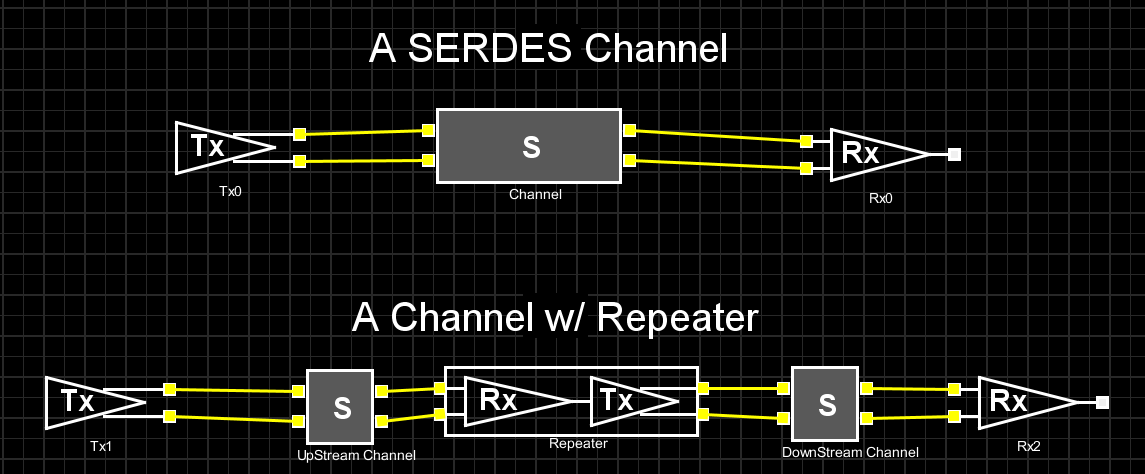
The picture above shows two common SERDES channel setups. While the one at the top has a direct connection between Tx and Rx, the bottom one has a “repeater” to cascade up stream and down stream channels together. This “cascading” can be repeated more than once so there maybe more than two channels involved. CTLE may sit inside the Rx of both set-ups or the middle “ReDriver” in the bottom one. In either case, the S-parameter block represents a generalized channel. It may contain passive elements such as package, transmission lines, vias or connectors etc. A characteristic of such channel is that it presents different losses across spectrum, i.e. dispersion.
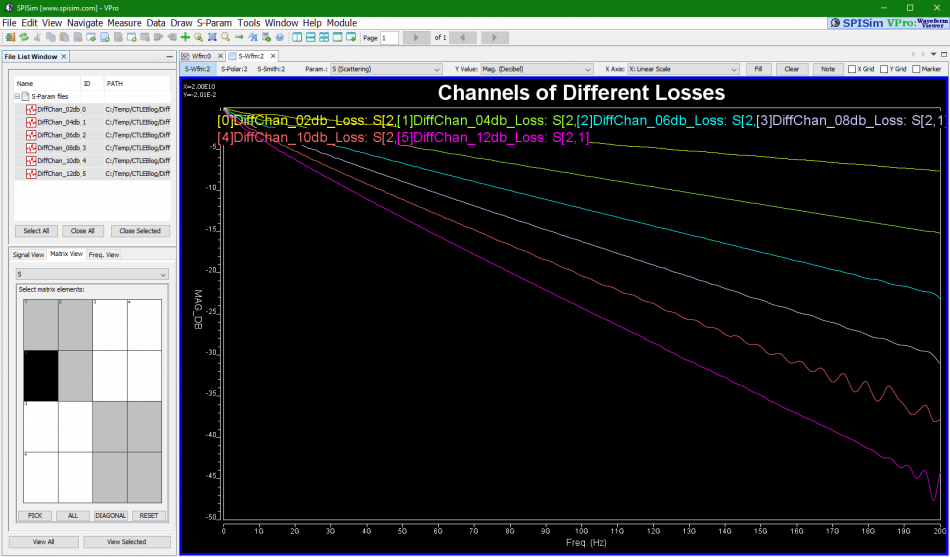
For example, if we plot these channel’s differential input to differential output, we may see their frequency domain (FD) loss as shown above.
Digital signals being transmitted are more or less like sequence of bit/square pulse. We know that very rich frequency components are generated during its sharp rising/falling transition edges. Ideally, a communication channel to propagate these signals should behave like an (unit-gain) all pass filter. That is, various frequency components of the signal should not be treated equally, otherwise distortion will occur. Such ideal response can be indicated as the green box below:

In reality, such all pass filter does come often. In order to compensate our lossy channels (as indicated by the red box) to be more like the ideal case (green box) as an end result, we need to apply equalization (indicated by blue box). This is why an equalizer is often used… basically it provides a transfer function/frequency response to compensate the lossy channel in order to recover the signal quality. A point worth taken here is that the blue box and red box are “tie” together. So using same equalizer for channels of different losses may cause under or over compensated. That is, an equalizer is related to the channel being compensated. Another point is that CTLE is just a subset of such linear equalizer.
A linear equalizer can be implemented in many different ways. For example, a feed-forward equalizer is often used in the Tx side and within DFE:
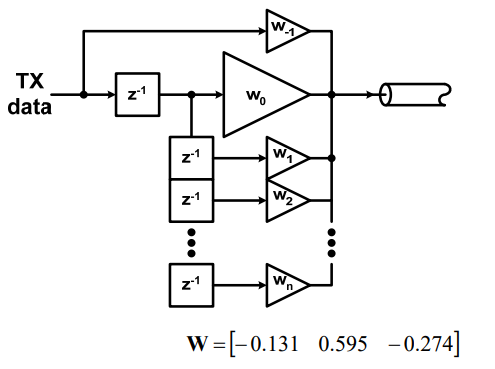
FFE’s behavior is more or less easier to predict and its AMI implementation is also quite straight forward. For example, a single pre-tap or post-tap’s FFE response can be easily visualized and predicted:
Now, a CTLE is a more “generalized” linear equalizer, so its behavior is usually represented in terms of frequency responses. Thus, to accommodate/compensate channels of different losses, we will have different FD responses for CTLE:
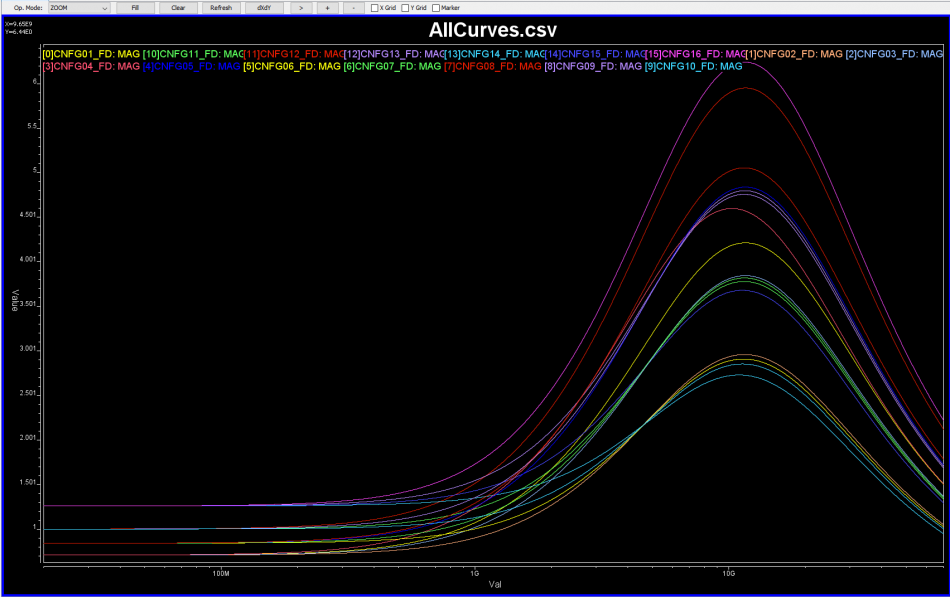
Now that IBIS-AMI modeling for CTLE is of concern, how do we obtain such modeling data for CTLE and how they should be modeled?
While CTLE’s behavior can be easily understood in frequency domain, for IBIS-AMI or channel analysis, it eventually needs to come back to time domain (FD) to convolve with inputs. This is because both statistical or bit-by-bit mode of link analysis are in time domain. Thus we have several choice: provide model FD data and have it converted to TD inside the implemented AMI model, or simply provide TD response directly to the model. The benefit of the first approach is that model can perform iFFT based on analysis’ bit rate and sampling rate’s settings. The advantage of the latter one is that the provided TD model can be checked to have good quality and model does not need to do similar iFFT every time simulation starts. Of course, the best implementation, i.e. like us SPISim’s approach, is to support both modes for best flexibility and expandability 🙂
Depending on the availability of original EQ design, there are several possibilities for FD data: Synthesized with poles and zeros, extract from S-parameters or AC simulation to extract response.
 So say if we are given a data sheet which has EQ level of some key frequencies like below:
So say if we are given a data sheet which has EQ level of some key frequencies like below: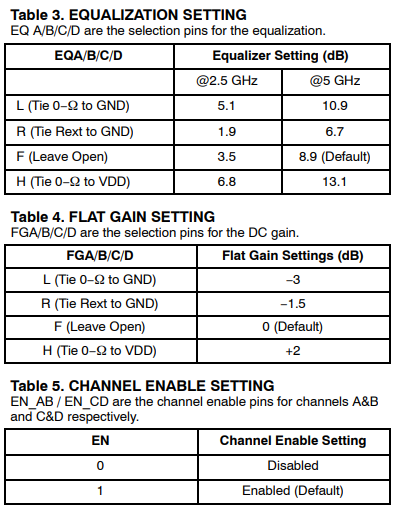 Then one can sweep different number and locations of poles and zeros to obtain matching curves to meet the spec.:
Then one can sweep different number and locations of poles and zeros to obtain matching curves to meet the spec.: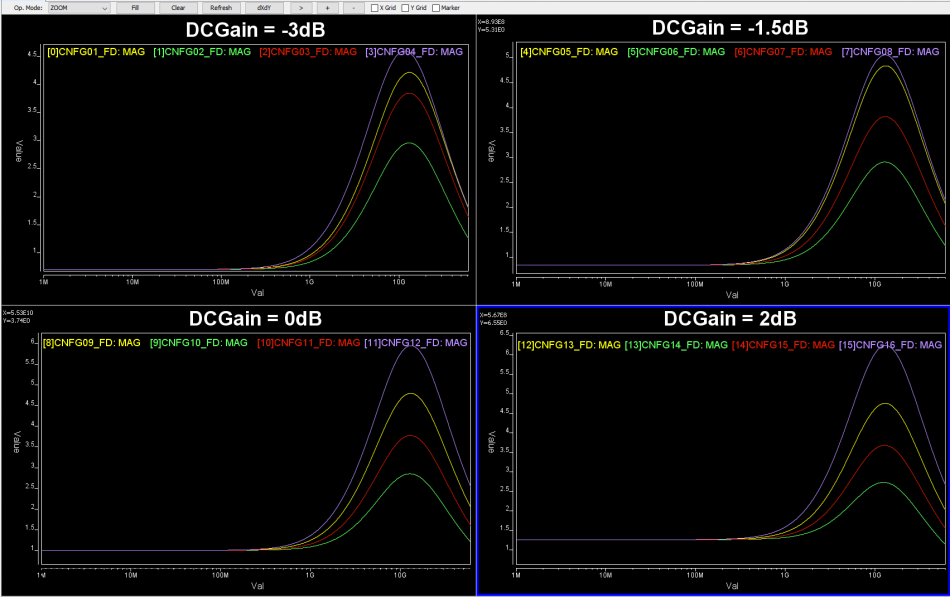 Such synthesized curves are well behaved in terms of passivity and causality etc, and can be extended to covered desired frequency bandwidth.
Such synthesized curves are well behaved in terms of passivity and causality etc, and can be extended to covered desired frequency bandwidth.

Now that we have data to model, how will they be implemented in C/C++ codes to support AMI API for link analysis is another level of consideration.
Typically, such adaptive mechanism has a pre-sorted CTLE in terms of strength or EQ level, then a figure-of-merit (FOM) needs to be extracted from equalized signal. That is, apply a tentative CTLE to the received data, then calculate such FOM. Then increase or decrease the EQ level by using adjacent CTLE curves and see whether FOM improves. Continue doing so until either selected CTLE “ID” settles or reach the range bounds. This process may be performed across many different cycles until it “stabilized” or being “locked”. Thus, the model may need to go through training period first to determine best CTLE being used during subsequent link analysis.
So now you have a bunch of settings or data like below, how should you architecture the model properly such that it can be extended in the future with revised CTLE response or allow user to perform corner selections (which essentially adds another dimension):
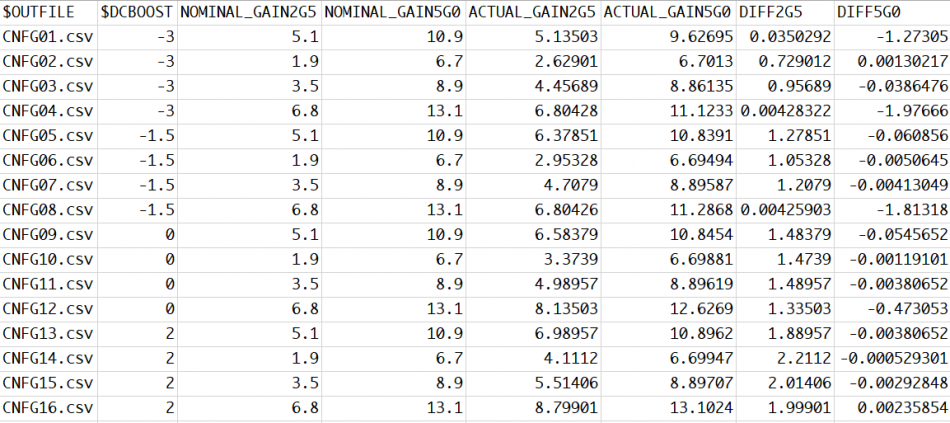
This is now more in software architecture domain and needs some trade-off considerations. For example, you may want to provide fine grid full spectrum FD/TD response but the data will may become to big. So internal re-sampling may be needed. For FD data, the model may needs to sample to have 2^N points for efficient iFFT. Different corner/parameter selection should not be hard coded in the models because future revised model’s parameter may be different. For external source data, encryption is usually needed to protect the modeling IP. With proper planning, one may reuse same CLTE module in many different design without customization on a case-by-case basis.
Finally it’s time to correlate the create CTLE AMI model against original EQ design or its behavioral model. Done properly, you should see signals being “recovered” from left to right below:
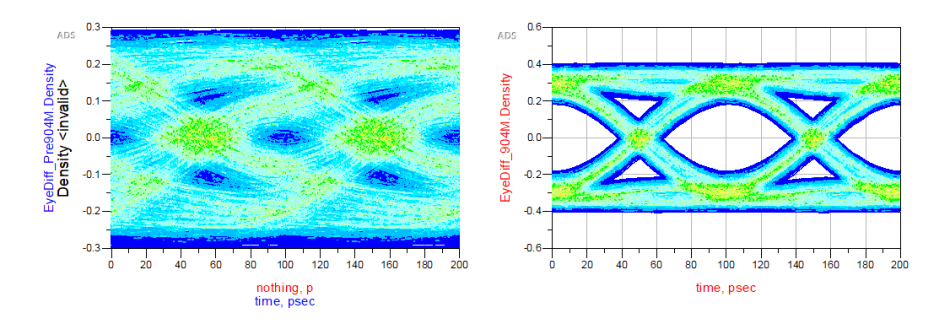
However, getting results like this in the first try may be a wishful thinking. In particular, the IBIS-AMI model does not work alone… it needs to work together with associated IBIS model (analog front-end) in most link simulator. So that IBIS model’s parasitics and loading etc will all affect the result. Besides, the high-impedance assumption of the AMI model also means proper termination matching is needed before one can drop them in for direct replacement of existing EQ circuit or behavioral models for correlation.
At this point, you may realize that while a CTLE can be easily understood from its theoretic behavior perspective, its implementation to meet IBIS-AMI demands is a different story. We have seen CTLE models made by other vendor not expandable at all such that the client need to scratch the existing ones for minor revised CTLE behavior/settings (also because this particular model maker charges too much, of course). It’s our hope that the learning experience mentioned in this post will provide some guidance or considerations regardless when you decide to deep dive developing your own CTLE IBIS-AMI model, or maybe just delegate such tasks to professional model makers like us 🙂
System channel is usually represented in S-parameters. They can be extracted in frequency domain using a 3D field solver, and/or cascaded stage by stage using tool like SPISim’s SPro. With LTI (linear time invariant) assumption, it’s possible to synthesize eye or BER plot of millions of bits using statistically analysis… using single time domain pulse for these parameters. However, it’s still often desired to be able to simulate the s-parameter in time domain for defined bit patterns. Thus, a system simulator like our SSolve must be able to support such requirement. In addition, one may also want to know the frequency response when given a broadband spice converted spice elements, such as via, package or connector models. So the reversed process, i.e. extract S-parameters from spice elements, is also often required. In this post, we will briefly talk about how these may be developed in simulator like SSolver.
S-Element… S-Parameters:
There have been many conference and journal papers proposing different methods of simulating S-parameter in time domain. However, at the most basic level, S-parameter can be considered as a transfer function or filter block. Thus DSP techniques can apply: transfer function multiplying inputs in frequency domain can be converted into time domain using convolution:
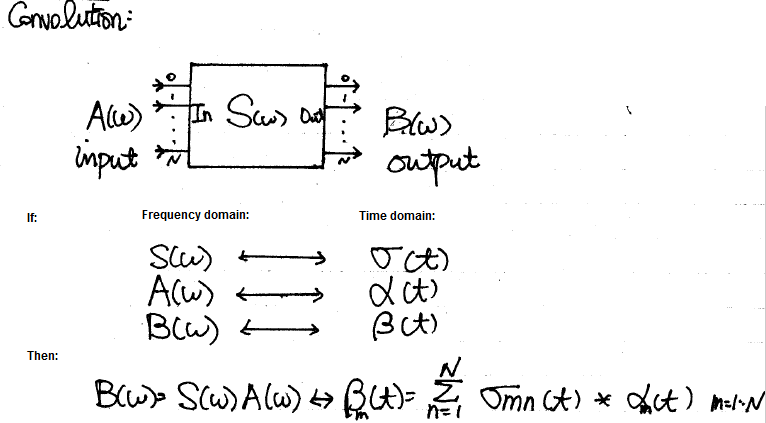
The time domain at the right hand side can be further separated into two parts: history up to this time point (integrate from -infinity to t=n-1) and the value at this particular moment t=n due to input. The first part is a constant as it’s already happened in the past and can’t be changed, the second part is, however, input dependent and must be updated within the “solve” and “stamp” hot loop inside newton iteration. When putting together, they form a Norton circuit form of I = Y * V + J where Y is value affected at this moment and J, a constant, is due to past history. This Norton form can then be “stamped” accordingly for matrix solving.
Interested reader may refer to the paper published by HP linked below for detailed explanations and math:
Integration of Transient S-Parameter Simulation into HSpice
The equation [18] and [19] is the aforementioned Norton equivalent circuit form and can be used accordingly.
The convolution method needs to update history with the solved results of this time step for next time step to be used. In addition, the basic convolution requires that the dt to be constant, thus a variable time step simulation will be greatly hampered by this requirement in terms of performance. So the convolution modeling has rooms for improvement.
One of the possible approach is using vector fitting technique mentioned in previous post about “W-element” modeling. With the S-parameter data in frequency domain, one may construct a Pade approximation using several poles and zeros. Then basis functions can be created for each of the pole in time domain and simulate accordingly. A benefit of this process is that the constructed form is a rational function which is guaranteed to be causal. So if there are issue regarding causality of the provided s-parameter, it can be fixed during the modeling process. Lastly, due to exact fitting of multi-port s-parameter across the frequency spectrum are not likely, some sort of error minimization (in the MSE sense) is needed to have a balance between accuracy and number of poles.
P-Element… Port element:
Often times after a package, connector or via modeling engineer created a model, he or she will use tool like broadband spice to convert such 3D extracted s-parameters to spice equivalent circuit composed of various basic elements. When a system designer or SI engineer receive such converted models, the original S-parameter may not be available already. Rather than insert this model into the channel and simulate blindly, it’s often beneficial to be able to reconstruct and inspect the model’s frequency domain response first before actually using them. S-Parameter extraction via simulation is basically a form of AC simulation, thus with AC model of the system elements constructed, the S-Parameter extraction part becomes easy.
The context here is small signal S-parameter extraction, thus all the AC signal is done very close to the operating point. That is, a DC solution needs to be obtained first for each port’s respecitve bias condition, then the AC stimulus is applied and solve for each frequency point.
A “Port” or “P-element” has several properties: dc bias condition, reference impedance, port-name and port-order. For a multi-port s-parameter extraction, one port is excited at a time with specified dc bias value. AC sweep is then performed while the other ports are terminated to their reference impedance. The power wave of input and output, measured and processed using current injection and nodal voltage measured, can then obtained for this input to the other output ports. Using simple math described in the link below:
S-parameter measurements
one can obtain S-parameter of Sij (i is port with input stimulus, j are the other ports) content easily this way. Repeat the same process for the other ports one at a time (with their respective dc bias condition) and the full S-parameter can be obtained. Finally, the order of ports are arranged according to the port properties, their respective port name are written out at the top of the touch stone file and the process is complete. Should there be needs to convert to other formats such as Y, Z parameter (sometimes good for checking connectivity), one can do so easily with formula (assuming generalized 2-N ports) or simply use developed tool like our SPro.
Back to the top:
Back from these modeling physics to the computer science domain, one also need to consider the following topics when doing simulator development:
While the list can go on and on and the tasks may be daunting, the end results are definitely worthy to the analysis flow and methodologies development. With developed simulator, there is no longer absolute need to form a close-loop formula or equation in order to solve circuit equation. The module or flow running on top can simply create netlist and have this simulator solved for you. Not to mentioned this also make maintenance and testing much easier. For an EDA company like us, I would say this is a journey worth taking.
When modeling device for a circuit simulator, the raw netlist input needs to be converted into internal structure first, then a physical model is constructed during the “modeling” phase, and corresponding equivalent Norton or Thevenin circuits’ parameter are solved within each Newton iteration at each timestep. The solved parameters are finally “stamped” into system matrix for Newton iteration solving. “Model” and “Solve” is the essential part of device modeling for a circuit simulator and that’s whey “Physics” come into play.
In these two posts, we will briefly talk about how system devices, in particular IBIS, Transmission line and S-parameter are “modeled” and “solved”.
B-Element… IBIS:
Looking at the IBIS’s structure, the modeling part is actually quite straight forward:
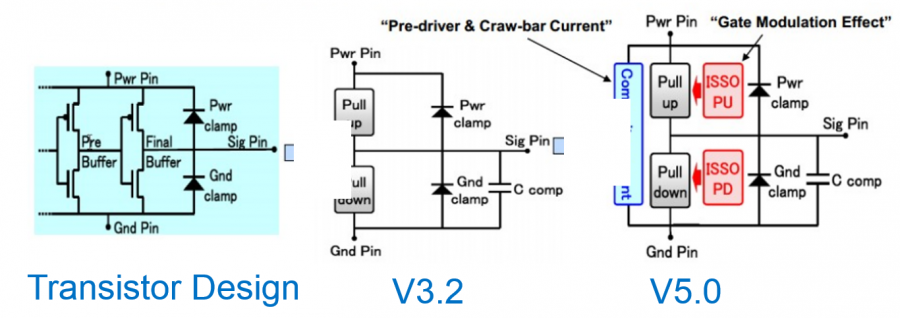
The four IV curve data: pull-up, pull-down, power clamp and ground clamp act like non-linear resistors. With terminal voltage known within each Newton iteration, the conductance can be look-up from these curve tables and obtained using linear interpolation.
The switching coefficients and composite currents are both time dependent. Their values are calculated in the “modeling” phase when simulation has not even started. The obtained coefficients is a multiplier which will further scale the conductance calculated for IV data and thus stamped value. These scaling are such that when test load specified in the waveform section is connected, driver at the pin will reproduce exactly the same waveform data given in the model. As to C-Comp, it can be inserted using simulator’s existing infrastructure so the integrator there will manage the stamping and error prediction.
The more complicated portion of IBIS modeling inside a simulator is due to the options available for the end user, thus model developer must plan in advance. For example, the c_comp may be split across different terminals. Each waveform, IV or components have different skews which book-keeping codes must take care of. There might be added submodel for pre-emphasis or de-emphasis so the class implementation-wise one should consider “composite” pattern such that recursive inclusion can happen. At the end, this is a relative simple device to model for simulator, particular when comparing to the transmission line.
W-Element… Transmission line:
Every electromagnetic text book will give transmission line structure as shown below:
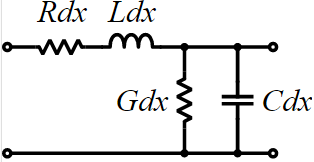
This is an uniform distributed model and is implemented early in various simulators as the “U” element. While implements T-Line model this way is now outdated due to the performance issue, it’s still how the T-Line’s raw data, frequency dependent tabular model, are given:
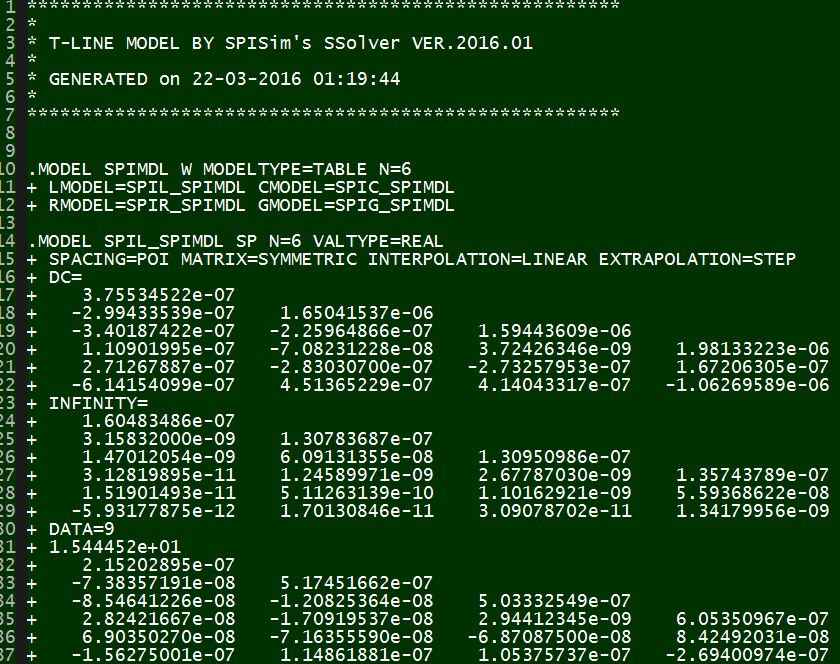
The tabular model are field solved of Maxwell’s equations based on layer stackup, trace layout, material properties and sometime special treatment (like surface roughness) and finally presented as R/L/G/C data at low (DC), high (Infinity) frequencies and many points in between. Thus to model T-Line for a simulator to use, one has to convert these data to a mathematical form first which can then be used in either time or frequency domain. For transmission line, this can starts with Telegrapher’s equations.
By solving the KCL/KVL of a unit length RLGC circuit above, one can derive and find the telegrapher’s equation:
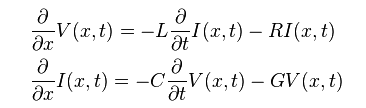
And the solution to this equations, as explained in the wiki link above, involve a wave propagation function Gamma:
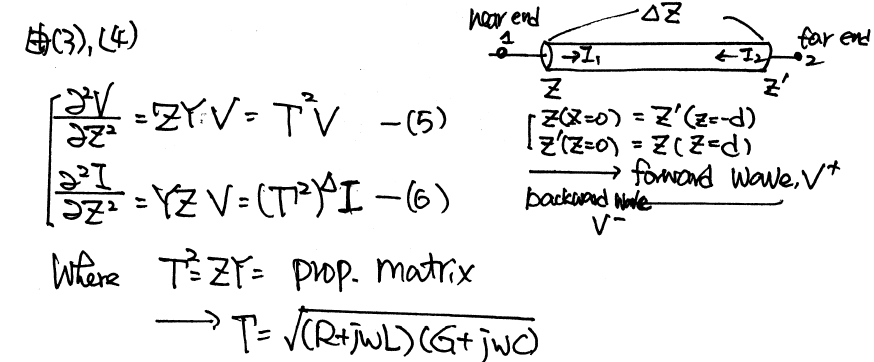
When realize this in the system model, it as the Norton equivalent circuit form:
So on each side (near end and far end) of the transmission line, there are two components: Z (admittance) at that particular time step and current source due to the propagation delay originated from the other end. These two components (Z(s) and r(s)) can be obtained from the tabular data in frequency domain and then converted to integrate-able form in time domain so that they can be “stamped”. Generally, it includes the following steps:
For the first three steps, I wrote a simple matlab codes to demonstrate how how they are done:
Impedance function: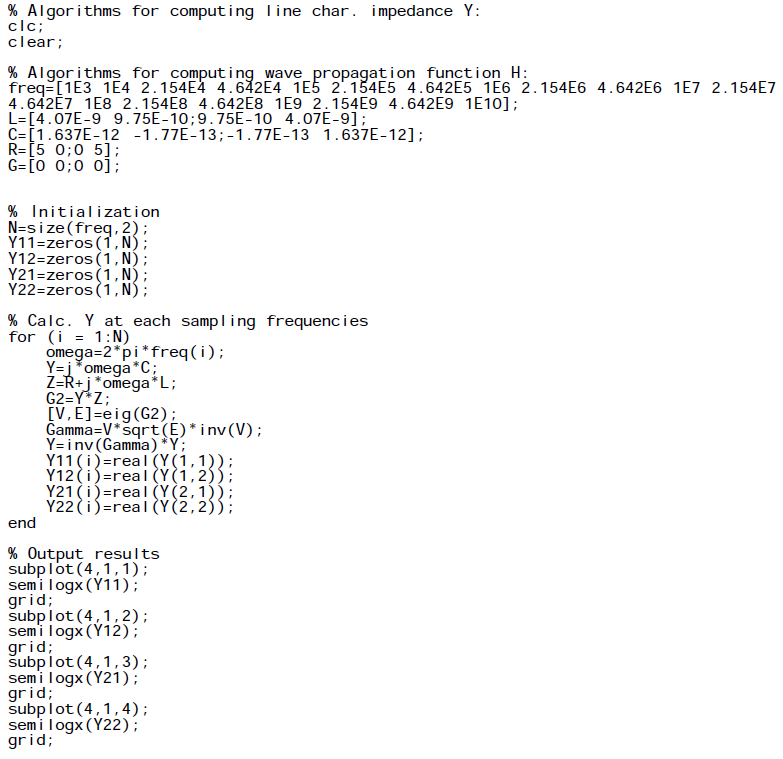
Propagation function: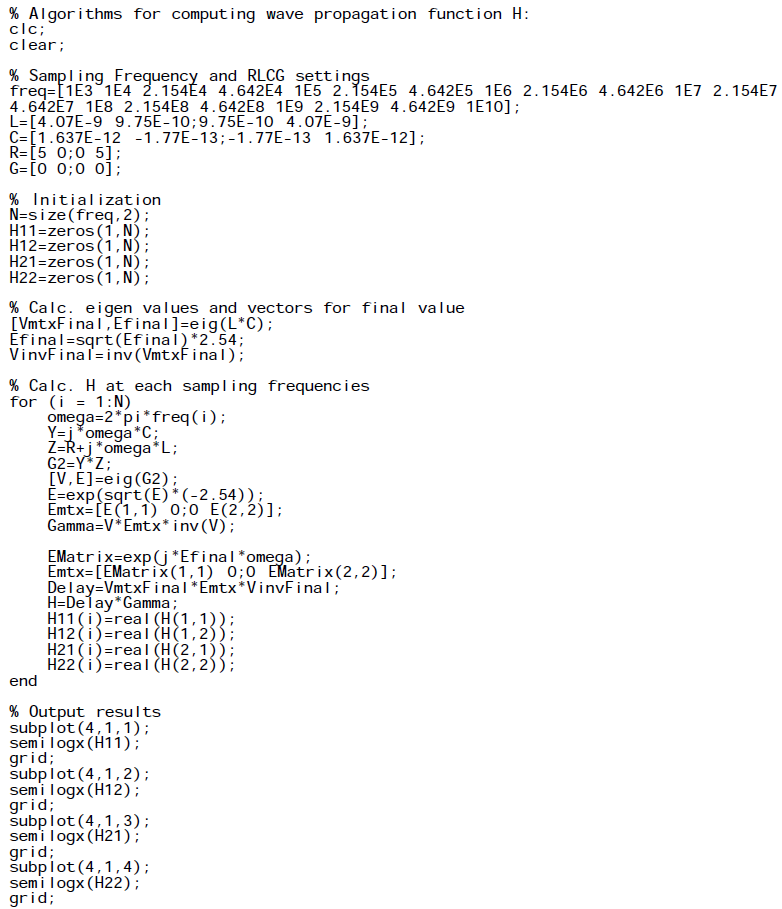
Plots: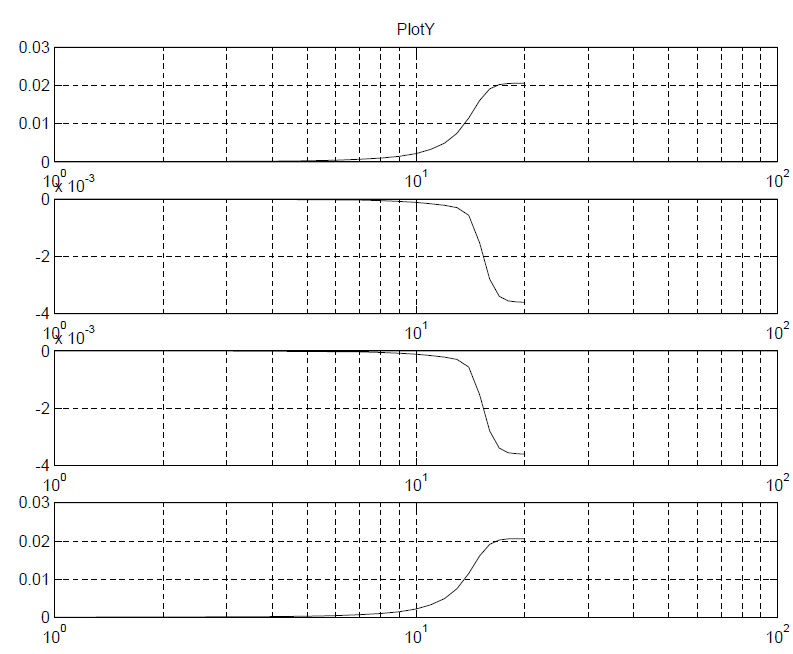
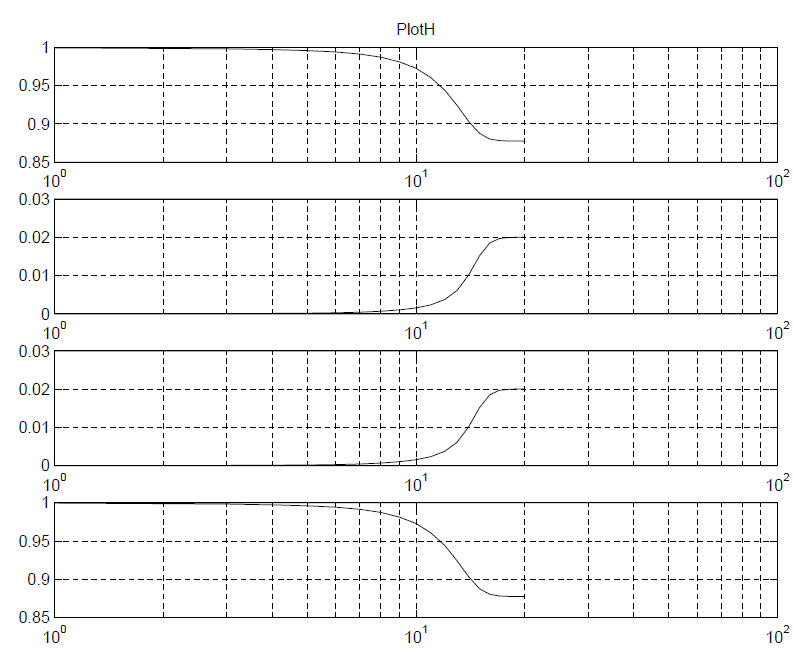
While the matlab codes above seems straightforward, most simulator (including SPISim’s SSolver) will program with native codes (C/C++) for performance consideration. So a whole lots of matrix operation (inverse, eigen value, LU decomposition etc) will also come into play during the process.
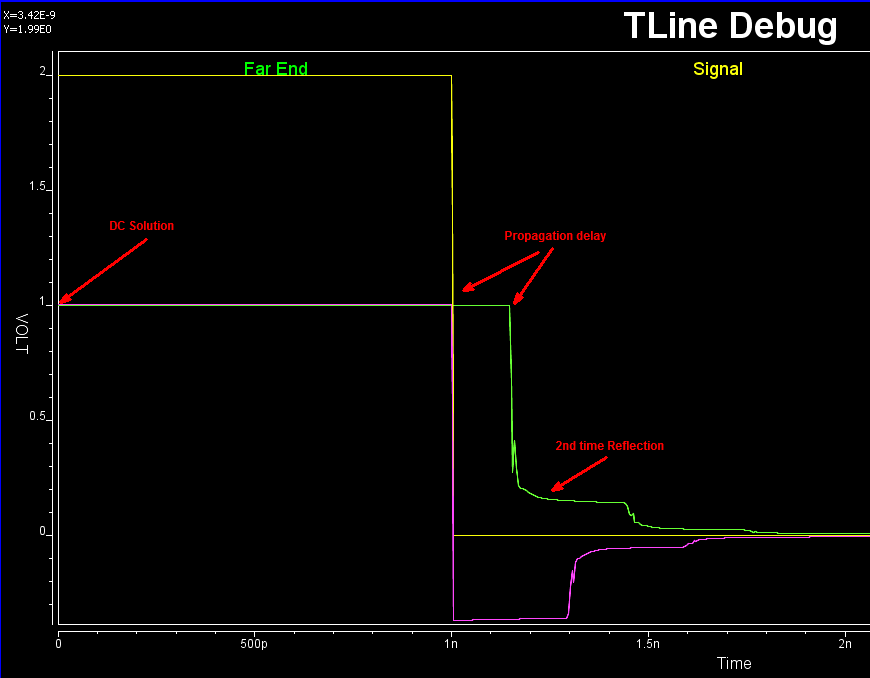
It’s rarely the case that the developed model or codes will work the first try. With so many terms (of converted poles and zeros) for so many dimensions (coupled cases), it’s a daunting task to figure out what has gone wrong when waveform is not as expected. It’s often simpler to back to basic: check steady state solution first, use one line, no reflection with by matching impedance at the other end, use characteristic impedance to find nominal reflection value and so on to help identifying the issue:
Interested reader may find more details about SPISim’s implementation, same as HSpice’s, in the following paper:
“Optimal Transient Simulation of Transmission Lines” by Dmitri Borisovich Kuznetsov, Jose E. Schutt-Aine, IEEE Trans. on Circuit and Systems, I Feb. 1996
In terms of book, I have found that Chap. 5 of Dan Oh’s “High-speed Signaling” book, S6 in our reference book section, give best explanations among others. This maybe because Mr. Oh is from UIUC around the same time when the paper was published as well 🙂 It also worth mentioning that similar technique can be applied to other passive, homogeneous device modeling, such as the system channel. For example, one common approach of checking and fixing casual issue of a s-parameter is by using vector fitting and convert to rational function form.