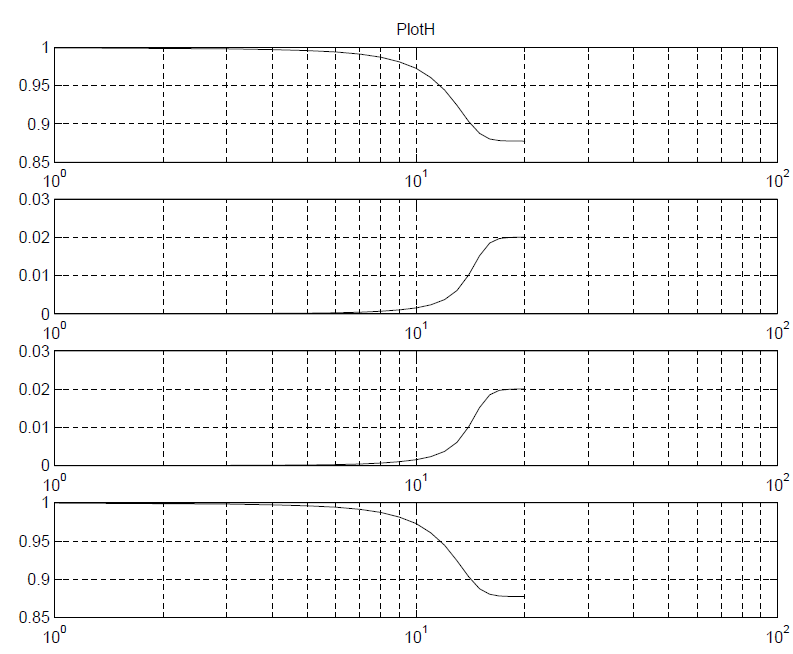
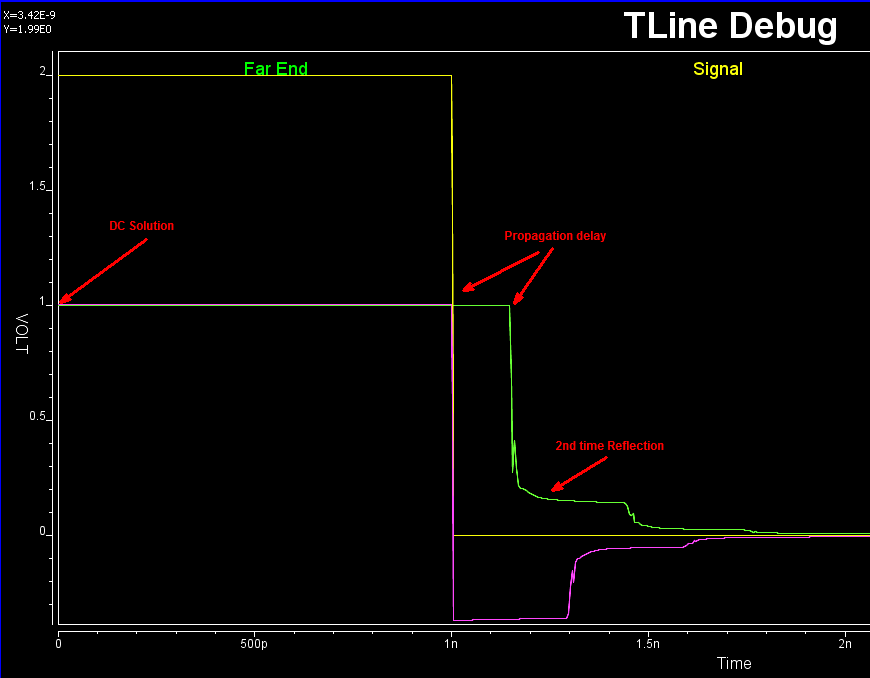
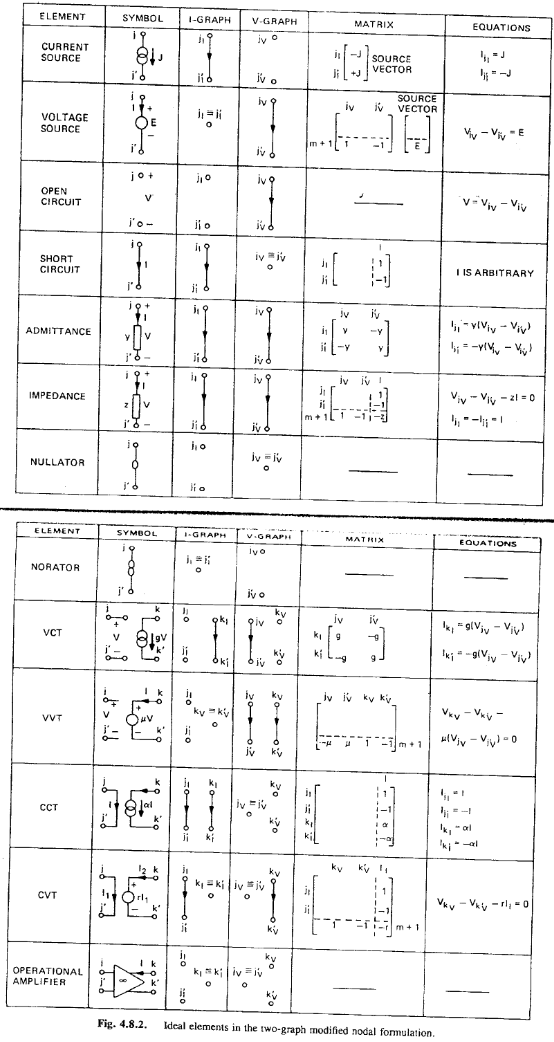
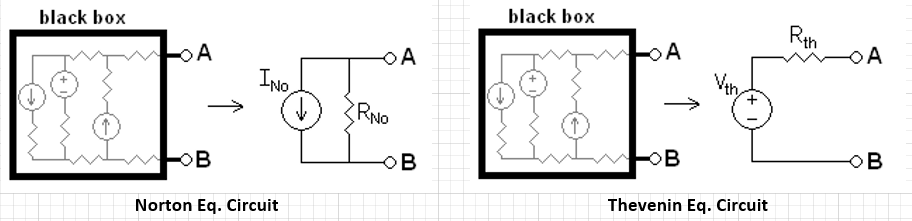
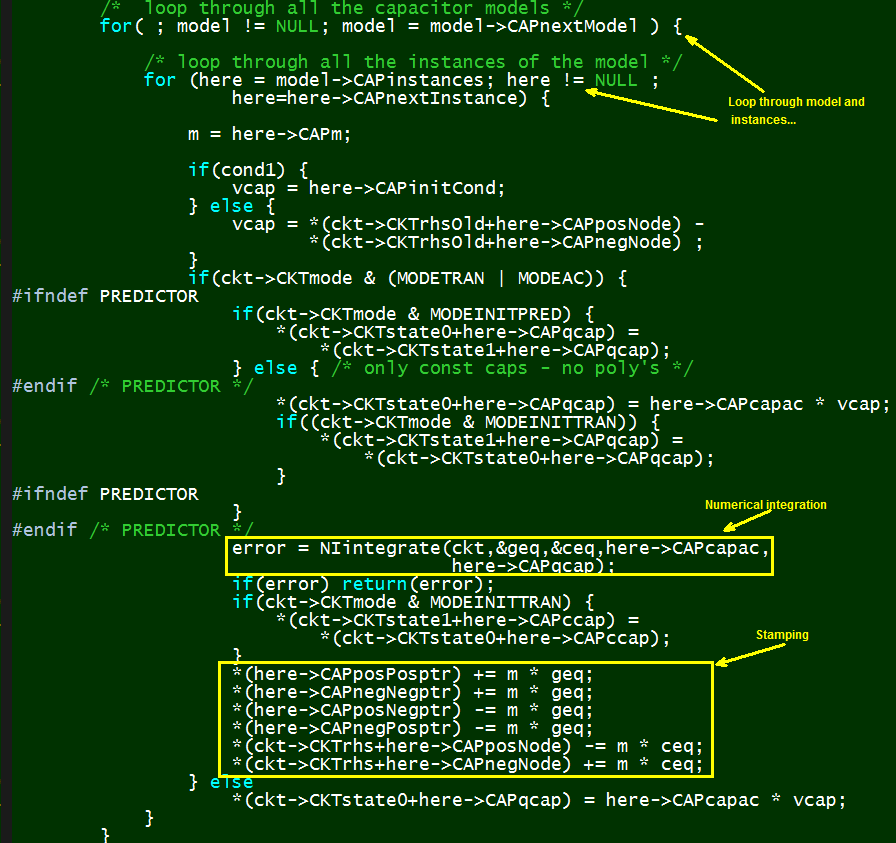
System channel is usually represented in S-parameters. They can be extracted in frequency domain using a 3D field solver, and/or cascaded stage by stage using tool like SPISim’s SPro. With LTI (linear time invariant) assumption, it’s possible to synthesize eye or BER plot of millions of bits using statistically analysis… using single time domain pulse for these parameters. However, it’s still often desired to be able to simulate the s-parameter in time domain for defined bit patterns. Thus, a system simulator like our SSolve must be able to support such requirement. In addition, one may also want to know the frequency response when given a broadband spice converted spice elements, such as via, package or connector models. So the reversed process, i.e. extract S-parameters from spice elements, is also often required. In this post, we will briefly talk about how these may be developed in simulator like SSolver.

S-Element… S-Parameters:

There have been many conference and journal papers proposing different methods of simulating S-parameter in time domain. However, at the most basic level, S-parameter can be considered as a transfer function or filter block. Thus DSP techniques can apply: transfer function multiplying inputs in frequency domain can be converted into time domain using convolution:

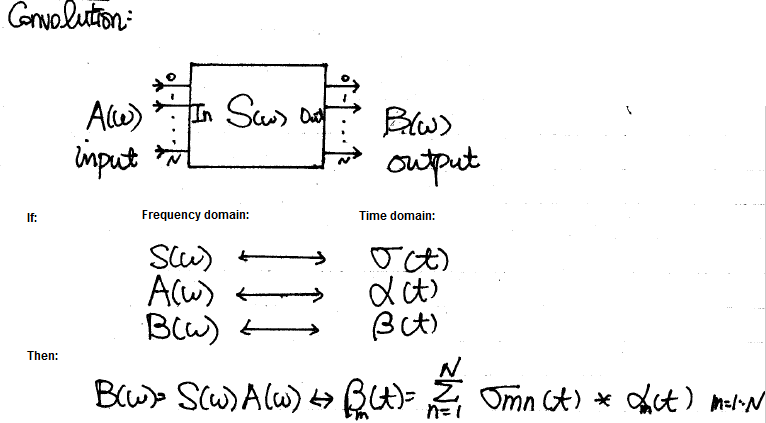
The time domain at the right hand side can be further separated into two parts: history up to this time point (integrate from -infinity to t=n-1) and the value at this particular moment t=n due to input. The first part is a constant as it’s already happened in the past and can’t be changed, the second part is, however, input dependent and must be updated within the “solve” and “stamp” hot loop inside newton iteration. When putting together, they form a Norton circuit form of I = Y * V + J where Y is value affected at this moment and J, a constant, is due to past history. This Norton form can then be “stamped” accordingly for matrix solving.

Interested reader may refer to the paper published by HP linked below for detailed explanations and math:

Integration of Transient S-Parameter Simulation into HSpice

The equation [18] and [19] is the aforementioned Norton equivalent circuit form and can be used accordingly.

The convolution method needs to update history with the solved results of this time step for next time step to be used. In addition, the basic convolution requires that the dt to be constant, thus a variable time step simulation will be greatly hampered by this requirement in terms of performance. So the convolution modeling has rooms for improvement.

One of the possible approach is using vector fitting technique mentioned in previous post about “W-element” modeling. With the S-parameter data in frequency domain, one may construct a Pade approximation using several poles and zeros. Then basis functions can be created for each of the pole in time domain and simulate accordingly. A benefit of this process is that the constructed form is a rational function which is guaranteed to be causal. So if there are issue regarding causality of the provided s-parameter, it can be fixed during the modeling process. Lastly, due to exact fitting of multi-port s-parameter across the frequency spectrum are not likely, some sort of error minimization (in the MSE sense) is needed to have a balance between accuracy and number of poles.

P-Element… Port element:

Often times after a package, connector or via modeling engineer created a model, he or she will use tool like broadband spice to convert such 3D extracted s-parameters to spice equivalent circuit composed of various basic elements. When a system designer or SI engineer receive such converted models, the original S-parameter may not be available already. Rather than insert this model into the channel and simulate blindly, it’s often beneficial to be able to reconstruct and inspect the model’s frequency domain response first before actually using them. S-Parameter extraction via simulation is basically a form of AC simulation, thus with AC model of the system elements constructed, the S-Parameter extraction part becomes easy.

The context here is small signal S-parameter extraction, thus all the AC signal is done very close to the operating point. That is, a DC solution needs to be obtained first for each port’s respecitve bias condition, then the AC stimulus is applied and solve for each frequency point.

A “Port” or “P-element” has several properties: dc bias condition, reference impedance, port-name and port-order. For a multi-port s-parameter extraction, one port is excited at a time with specified dc bias value. AC sweep is then performed while the other ports are terminated to their reference impedance. The power wave of input and output, measured and processed using current injection and nodal voltage measured, can then obtained for this input to the other output ports. Using simple math described in the link below:

S-parameter measurements

one can obtain S-parameter of Sij (i is port with input stimulus, j are the other ports) content easily this way. Repeat the same process for the other ports one at a time (with their respective dc bias condition) and the full S-parameter can be obtained. Finally, the order of ports are arranged according to the port properties, their respective port name are written out at the top of the touch stone file and the process is complete. Should there be needs to convert to other formats such as Y, Z parameter (sometimes good for checking connectivity), one can do so easily with formula (assuming generalized 2-N ports) or simply use developed tool like our SPro.

Back to the top:

Back from these modeling physics to the computer science domain, one also need to consider the following topics when doing simulator development:

• Memory pool management (allocation, expansion and clean-up)
• Multi-threading consideration
• Plug-in architecture for future devices
• ….

While the list can go on and on and the tasks may be daunting, the end results are definitely worthy to the analysis flow and methodologies development. With developed simulator, there is no longer absolute need to form a close-loop formula or equation in order to solve circuit equation. The module or flow running on top can simply create netlist and have this simulator solved for you. Not to mentioned this also make maintenance and testing much easier. For an EDA company like us, I would say this is a journey worth taking.

When modeling device for a circuit simulator, the raw netlist input needs to be converted into internal structure first, then a physical model is constructed during the “modeling” phase, and corresponding equivalent Norton or Thevenin circuits’ parameter are solved within each Newton iteration at each timestep. The solved parameters are finally “stamped”  into system matrix for Newton iteration solving. “Model” and “Solve” is the essential part of device modeling for a circuit simulator and that’s whey “Physics” come into play.

In these two posts, we will briefly talk about how system devices, in particular IBIS, Transmission line and S-parameter are “modeled” and “solved”.

B-Element… IBIS:

Looking at the IBIS’s structure, the modeling part is actually quite straight forward:

The four IV curve data: pull-up, pull-down, power clamp and ground clamp act like non-linear resistors. With terminal voltage known within each Newton iteration, the conductance can be look-up from these curve tables and obtained using linear interpolation.

The switching coefficients and composite currents are both time dependent. Their values are calculated in the “modeling” phase when simulation has not even started. The obtained coefficients is a multiplier which will further scale the conductance calculated for IV data and thus stamped value. These scaling are such that when test load specified in the waveform section is connected, driver at the pin will reproduce exactly the same waveform data given in the model. As to C-Comp, it can be inserted using simulator’s existing infrastructure so the integrator there will manage the stamping and error prediction.

The more complicated portion of IBIS modeling inside a simulator is due to the options available for the end user, thus model developer must plan in advance. For example, the c_comp may be split across different terminals. Each waveform, IV or components have different skews which book-keeping codes must take care of. There might be added submodel for pre-emphasis or de-emphasis so the class implementation-wise one should consider “composite” pattern such that recursive inclusion can happen. At the end, this is a relative simple device to model for simulator, particular when comparing to the transmission line.

W-Element… Transmission line:

Every electromagnetic text book will give transmission line structure as shown below:

This is an uniform distributed model and is implemented early in various simulators as  the “U” element. While implements T-Line model this way is now outdated due to the performance issue, it’s still how the T-Line’s raw data, frequency dependent tabular model, are given:

The tabular model are field solved of Maxwell’s equations based on layer stackup, trace layout, material properties and sometime special treatment (like surface roughness) and finally presented as R/L/G/C data at low (DC), high (Infinity) frequencies and many points in between. Thus to model T-Line for a simulator to use, one has to convert these data to a mathematical form first which can then be used in either time or frequency domain. For transmission line, this can starts with Telegrapher’s equations.

By solving the KCL/KVL of a unit length RLGC circuit above, one can derive and find the telegrapher’s equation:

And the solution to this equations, as explained in the wiki link above, involve a wave propagation function Gamma:

When realize this in the system model, it as the Norton equivalent circuit form:

So on each side (near end and far end) of the transmission line, there are two components: Z (admittance) at that particular time step and current source due to the propagation delay originated from the other end. These two components (Z(s) and r(s)) can be obtained from the tabular data in frequency domain and then converted to integrate-able form in time domain so that they can be “stamped”. Generally, it includes the following steps:

• Parse and store the raw tabular model;
• Calculate the propagation delay and characteristic impedance using highest frequency data (or using extrapolation), these value will be used for interpolation later in time domain.
• Construct the Z(s) or Y(s) and the wave function r(s) shown in the system model. As transmission lines are usually coupled, these curves are multi-dimensional in frequency domain;
• Using vector fitting technique to represent this frequency domain functions using series of poles and zeros. In most of the cases, particular when the model data has insufficient bandwidth or low quality, exact fit is not possible with reasonable number of poles/zeros and thus best fit in the minimum-square-error sense needs to be performed.
• Once pole and zeros are found, they can be converted into time domain as different order of terms. All these terms combined together will form the Y(t) or r(t) in time domain. Pade’s approximation may be used here.
• During time domain simulation, use interpolation to find r(t)’s value in the past history (propagation delay ago) and use that data to construct the equivalent model of this end at this particular time point.
• For frequency domain analysis, vector fitting and conversion to integral form is not needed. The Y(s) and r(s) data can be used directly for stamping at this frequency with some interpolation.

For the first three steps, I wrote a simple matlab codes to demonstrate how how they are done:

Impedance function:

Propagation function:

Plots:

While the matlab codes above seems straightforward,  most simulator (including SPISim’s SSolver) will program with native codes (C/C++) for performance consideration. So a whole lots of matrix operation (inverse, eigen value, LU decomposition etc) will also come into play during the process.

It’s rarely the case that the developed model or codes will work the first try. With so many terms (of converted poles and zeros) for so many dimensions (coupled cases), it’s a daunting task to figure out what has gone wrong when waveform is not as expected. It’s often simpler to back to basic: check steady state solution first, use one line, no reflection with by matching impedance at the other end, use characteristic impedance to find nominal reflection value and so on to help identifying the issue:

Interested reader may find more details about SPISim’s implementation, same as HSpice’s, in the following paper:

“Optimal Transient Simulation of Transmission Lines” by Dmitri Borisovich Kuznetsov, Jose E. Schutt-Aine, IEEE Trans. on Circuit and Systems, I Feb. 1996

In terms of book, I have found that Chap. 5 of Dan Oh’s “High-speed Signaling” book, S6 in our reference book section, give best explanations among others. This maybe because Mr. Oh is from UIUC around the same time when the paper was published as well 🙂 It also worth mentioning that similar technique can be applied to other passive, homogeneous device modeling, such as the system channel. For example,  one common approach of checking and fixing casual issue of a s-parameter is by using vector fitting and convert to rational function form.