Preface:
During the weekly meetings of IBIS Advanced Technology Modeling (ATM) task group earlier this year, a participant proposed requirement of code signing the released IBIS-AMI models for identification and security consideration. While this direction was not pursued further at the end due to various considerations, several meeting attendees suggested it would be helpful if someone with experience in this process can share (e.g. at the IBIS summit etc). It just so happens that all SPISim’s digital downloads, including executable, patches and AMI models are digitally signed. Thus even though I am no computer security expert, I am writing this post to share some info. and our process for you, the AMI model maker, to consider. If you decide to go this route, this post may even help you saving hundreds or even thousands of dollars on certificate purchase (really!) So read on…
What is code signing:
According to the wikipedia [HERE], code signing is a process of digitally “signing” executables to confirm the software author and guarantee that the code has not been altered or corrupted since it was signed. That is, if say SPISim creates an application or an AMI model, digitally sign then release them, recipients will be able to verify that the binary files they have at hand, regardless how they obtained them, are the originals. (I will use “software” to represent both executable and AMI models from this point as they are all binaries with programs.) If the software’s content was tampered … such as becoming corrupted during downloading or injected with malicious instructions, the digital signatures of the software will no longer be valid. This will be detected by the operating system or UAC (user account control). The digital signature is embedded inside the software. It only guarantees the source of the files but not their behaviors. So software may still have bugs or crash… only that you know who is the author to blame 🙂
Code signing makes use of asymmetric cipher (public/private key) algorithm. The private key file, i.e. a certificate, is a platform neutral. However, the code signing process itself is platform dependent. So windows’ software needs to be signed on windows and so are on OSX. Linux is a little different on this aspect, you will find more info. about this at the wikipedia link above.
In the subsequent sections, I will be using windows platform as an example.
What does signed software look like:
If your software is unsigned… such as the application shown below, users will see a “Publisher Unknown” info with yellow background. This may raise a red flag depending on your company’s IT or computer’s UAC policy settings.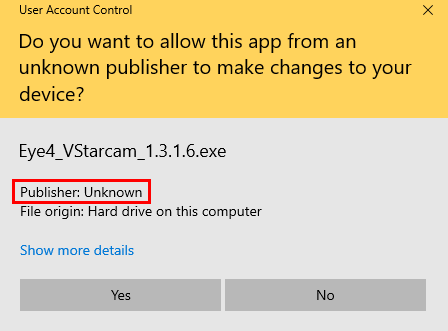
On the other hand, a signed application like ours will look like this (blue):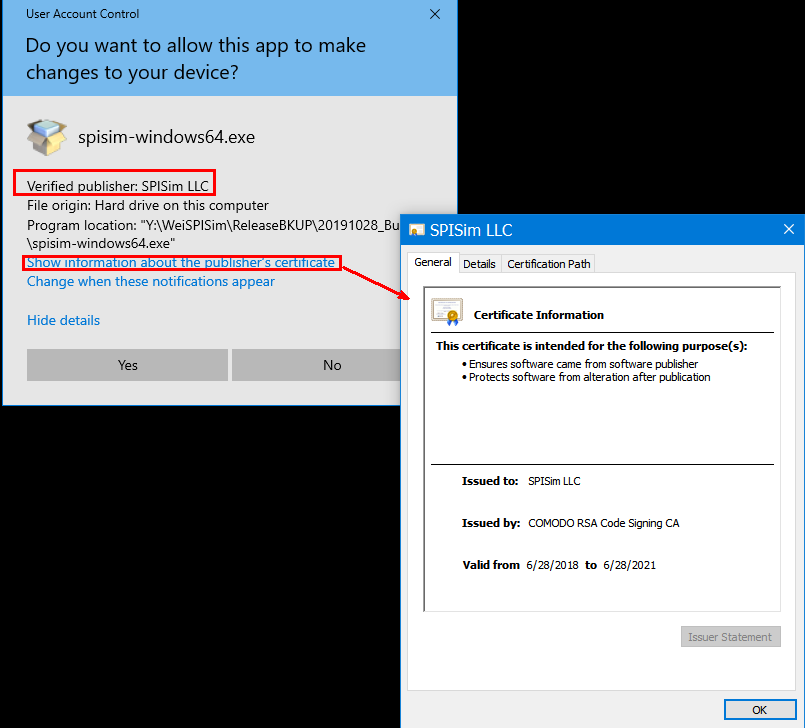
Besides showing “Verified”, more info such as company name, address, certificate issuer, valid periods etc are also available upon request as it’s embedded in the software.
Actually, as soon as you download a software application, you may right click to verify their “Digital Signatures”. Only signed binary will have such tab available: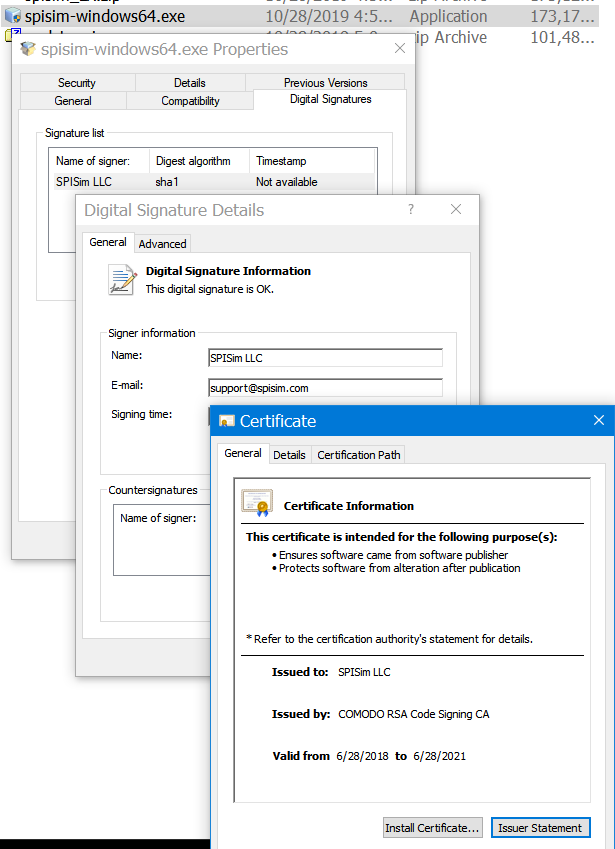
For signed web based application, such as our SPISim_AMI and SPISim_LINK free web apps, browser like chrome will let user run them directly. An unsigned or self-signed (more on this later) web-apps will mostly be blocked.
Regarding .dll (e.g. IBIS-AMI models), an unsigned one will not have any source info: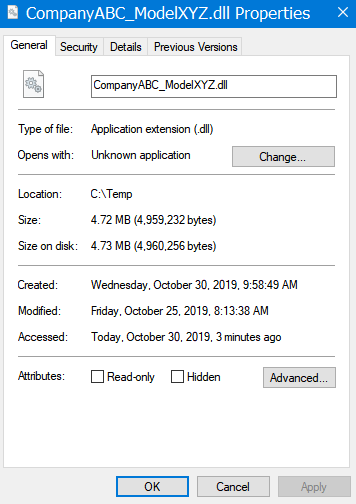
A signed one will look like this: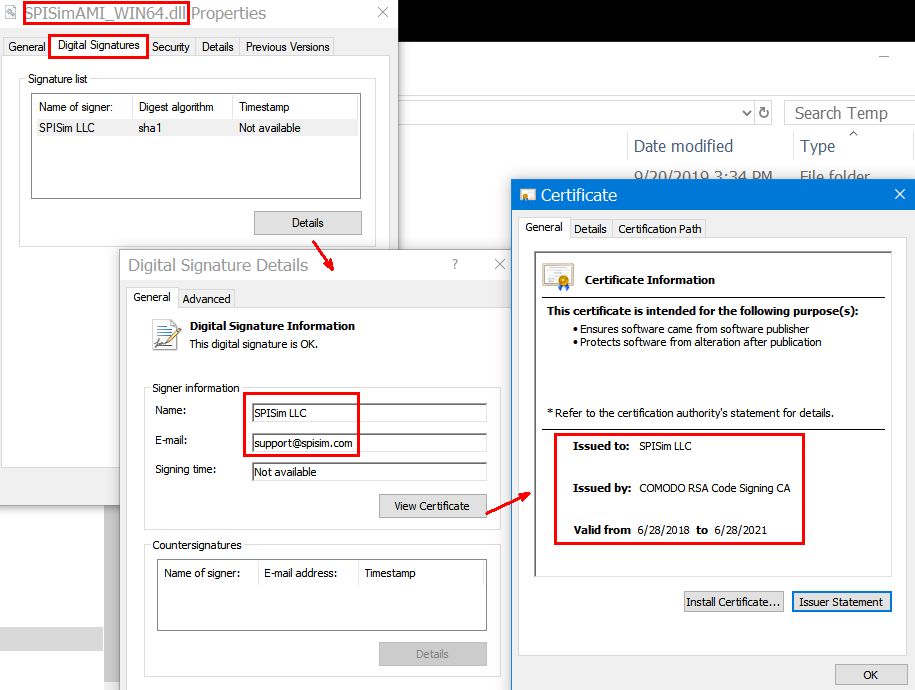
Why you should have your software signed:
For a desktop or server based application, platform mechanism such as windows’ UAC will detect the signature during the initial installation process. For a web-based application, browser serves as a gatekeeper to detect or even block unsigned ones being run as they present more/frequent dangers. For a .dll file such as IBIS-AMI model, users need to right-click the file and check its properties by themselves unless the application which loads these dlls will check first before executing APIs within. At this time point, I am not aware of any EDA tool or simulator which does so. Nevertheless, code signing your software is like putting a seal of approval. It makes your product look more professional and also shows that as a software or model publisher, you care about customers or clients’ cyber security when your product is being used.
How to have your software signed:
Now that you are interested in getting software signed, here are the process:
- Purchase a certificate:
You will need to have a certificate (i.e. private key) to sign the software. Your identity will be encrypted within this private key. Only a reputable entity can serve as a certificate authority (CA) and issue such certificate. One used to be able to create a self-signed certificate but that may be only useful within same organization (intranet). For public network, this entity will verify who you say you are before encrypting the identity you have provided using their own key (i.e. they vouch for your info) as a certificate. This is like a chain of trust. This way you can’t pretend that you are Microsoft or Google etc. This is a very involved process with human effort included so it may not be cheap!! By the way, a certificate is not forever… it expires after certain period of time.
If you search “purchase certificate for code signing” online, those top ones are probably quite expensive:
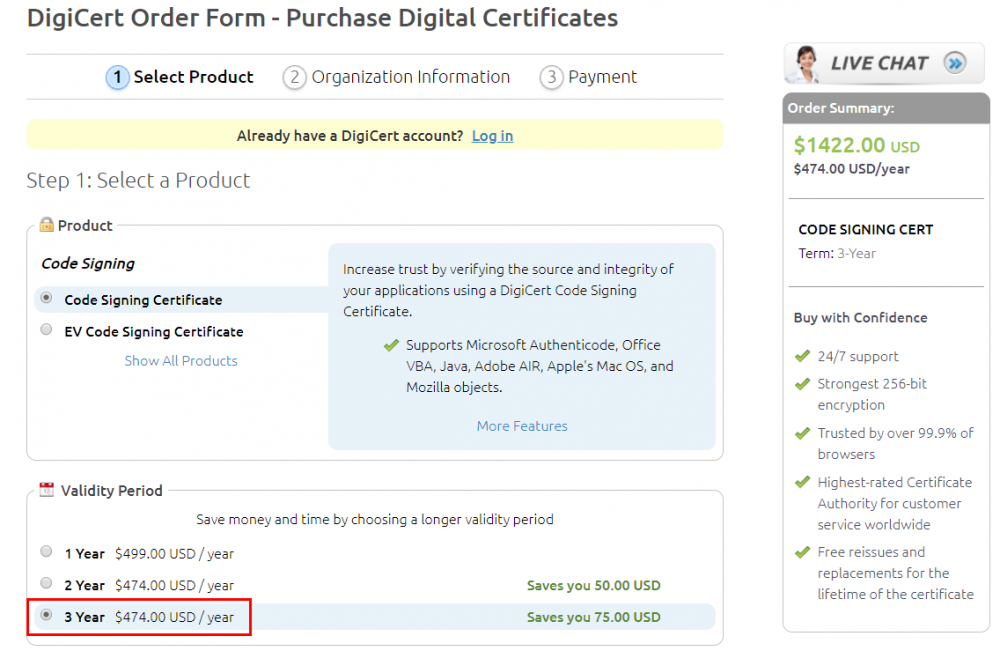
I am going to save you money here… Visit tucows.com, open an account and purchase certificate there. In stead of thousands, you pay less than two hundred for a three-year certificate!

- Validate your identification:
During the purchasing process, you will be asked to provide identity such as your personal or company name, company email address, phone number, phsical address etc. All the info. provided must be verifiable by this entity you are purchasing from. For example, you will need to have a public (government or state) record which shows same information. You may be asked to provide IDs and verify you are the domain owner. You will then be asked to wait for a period of time or even possible phone call from the CA. They will go through human based verification process to make sure the data you provided is valid and you are who you say you are. Only after that, they will email you the link to download/install the certificate they have issued for you. A supported web browser like FireFox is required to install the issued certificate.
For example, here is the info. requested during the purchasing process:

- Download and backup certificate
The issued certificate will delivered via a clickable link and can only be installed in the same browser used during application/purchasing process. It is very important that you install, export this certificate right away then backup to a different location. With backup certificate, you can use other computer to sign software or the same computer after OS re-install. You will also need this certificate as a file as part of the building and release process.
More info. about how to do this is available [HERE]
- Make code signing part of your build/release process
Once the certificate file is available, you may incorporate that into part of software releasing flow by signing and verifying the signature at the end of the building process. This is platform and OS-bit (32-bit or 64-bit) dependent. The white blocks below are password I used for using our certificate..
Signing and verify IBIS-AMI dll file: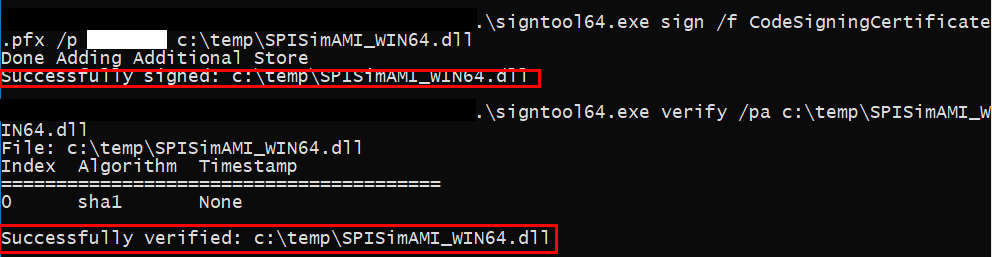
Signing web-app jar file: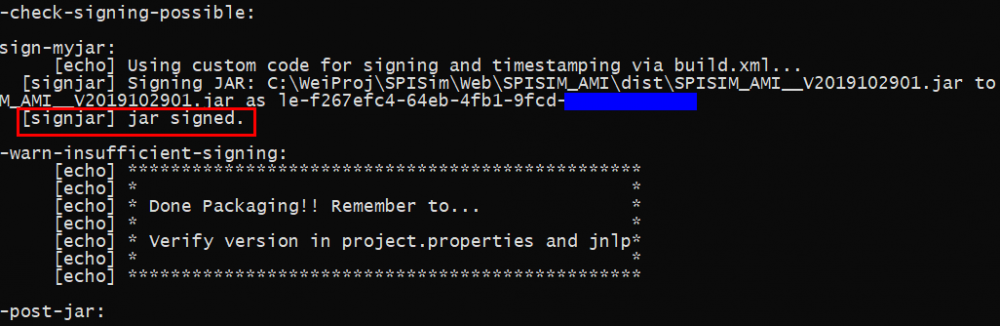
Signing and verify installer:
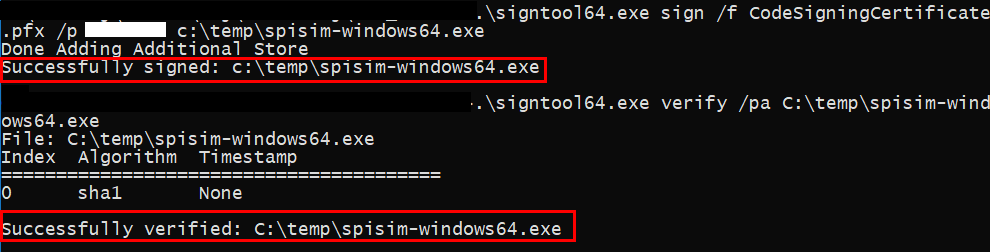
Time-stamp using a NNTP server is required:

Signtool64 above is a windows’s tool from Microsoft. Java has its own version: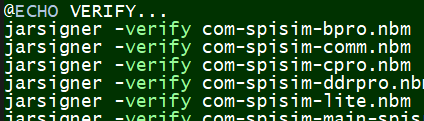
Unsign signed software:
Because a certificate is valid only though certain period of time(e.g. three years), it will “expire” after that. While not immediately after the expiration date, you will soon not be able to sign the software with expired certificate. The time-stamping via a time-server during the signing process is a mechanism to prevent you back-date the software to be released…. That means you will need to keep certificate updated by re-purchase a new one. Platform such as windows’ UAC may also prevent one from installing software signed by outdated certificate. The last possibility is that a certificate may be revoked due to the “chain of trust” being destroyed somewhere upstream.
More often than not, once an AMI model is released, it may stay out there beyond original publisher’s control for quite some time and then become expired. A signed software can be un-signed to strip this timestamped signature if the IT policies prohibit installing outdated binaries: More info. may be obtained [HERE]
Finally:
I hope this blog post will be helpful for model maker publishing their AMI models or software alike. Another good blog article on this topic may be found [HERE]









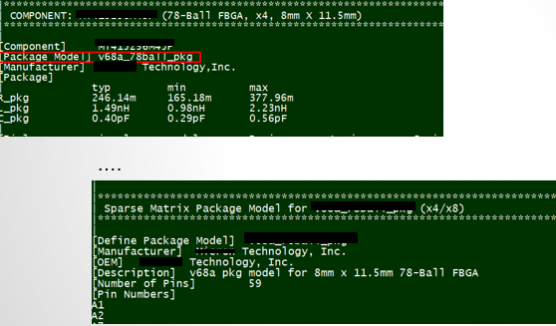
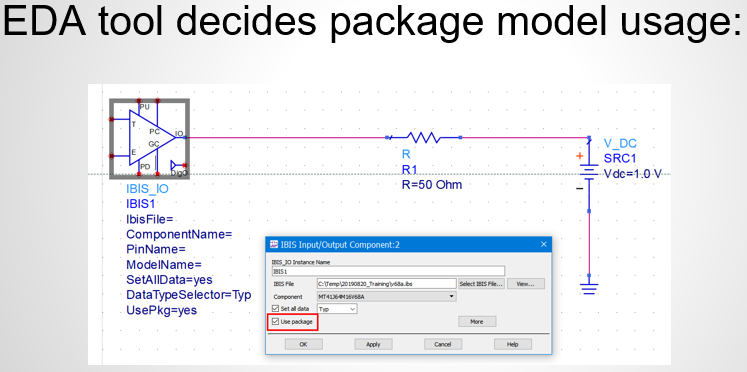


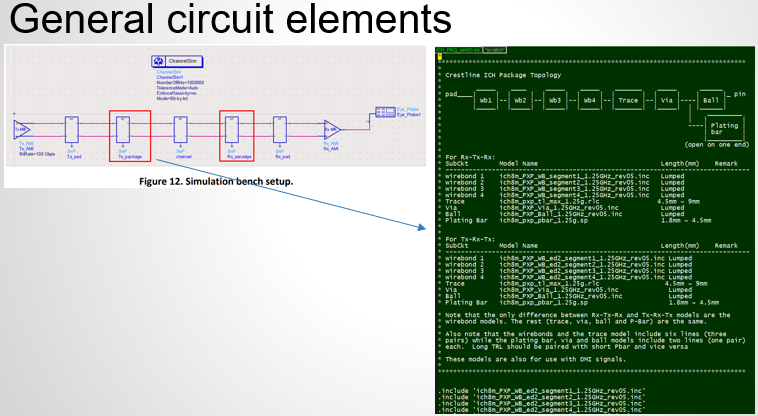
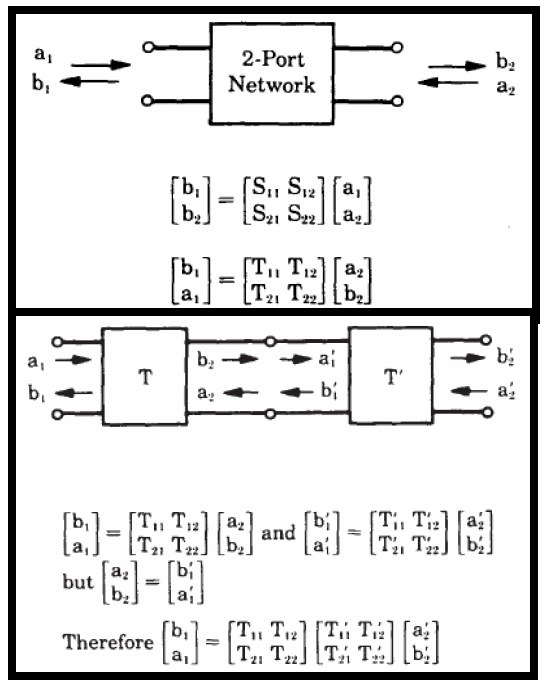
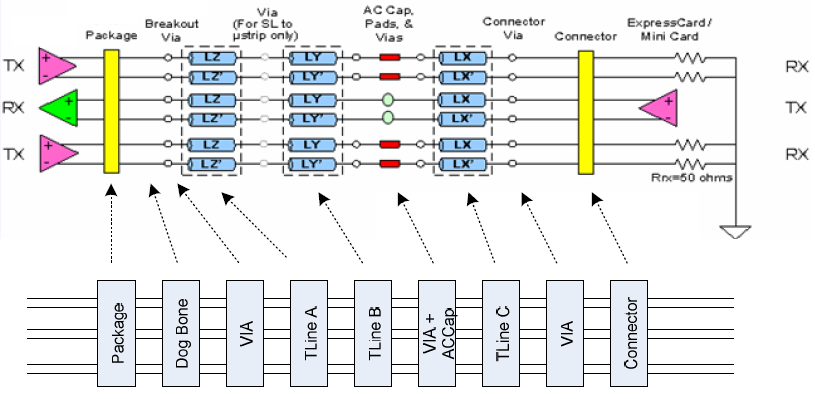
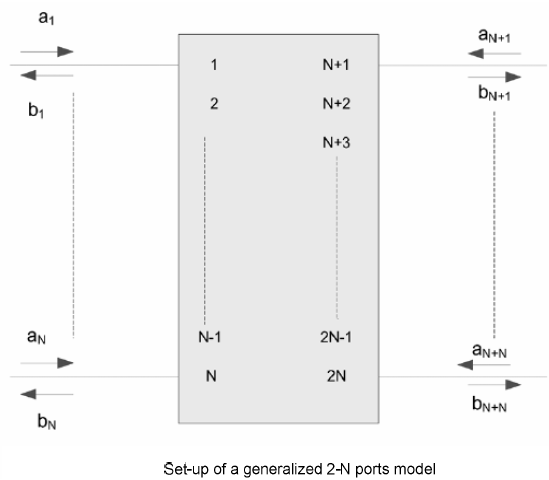

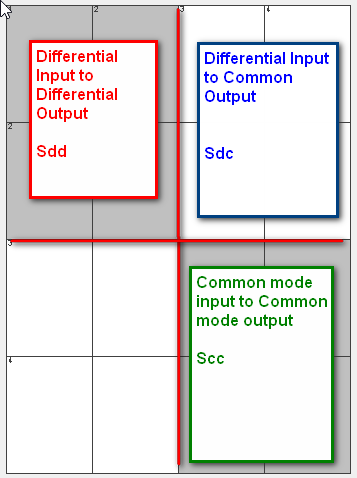
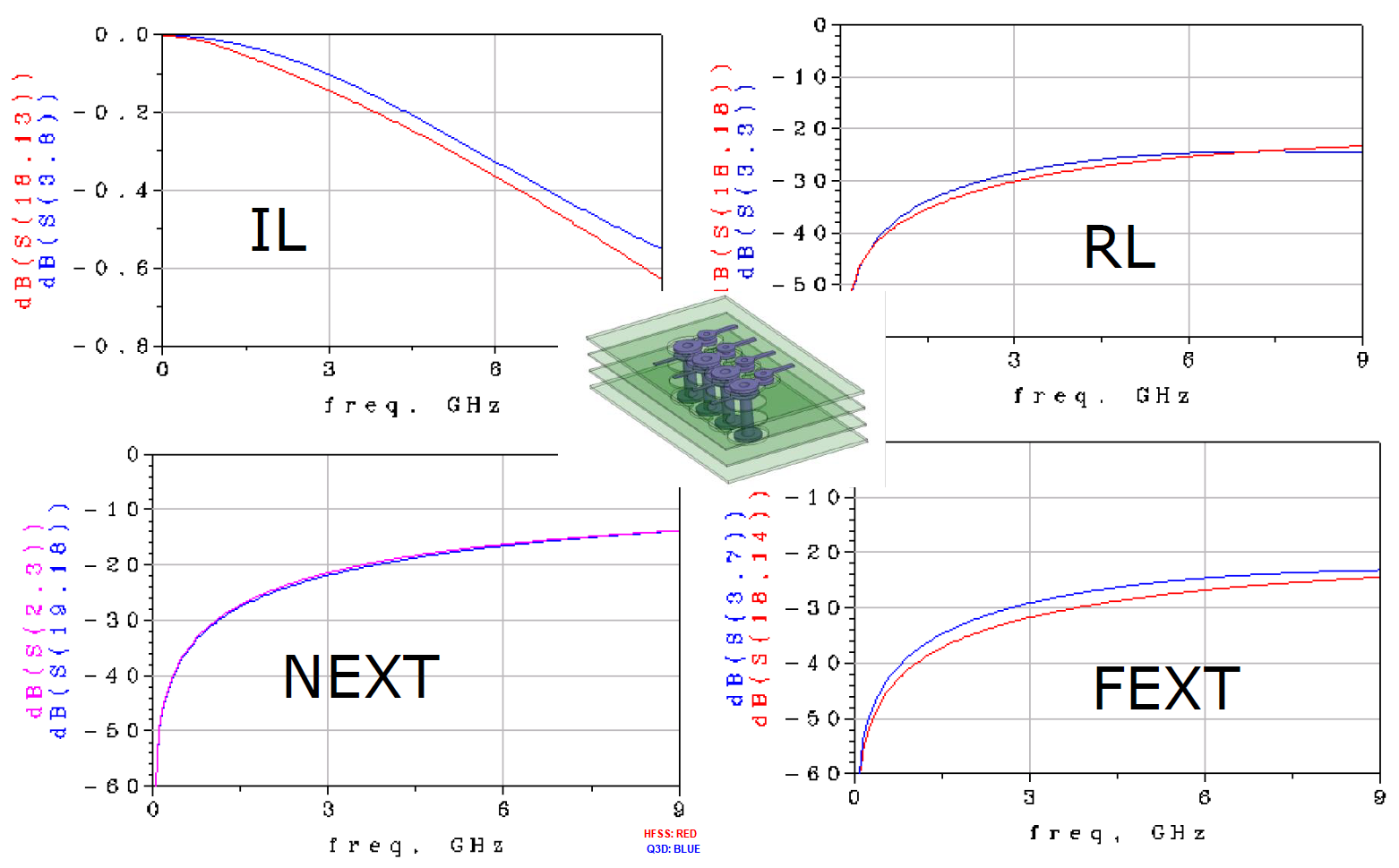
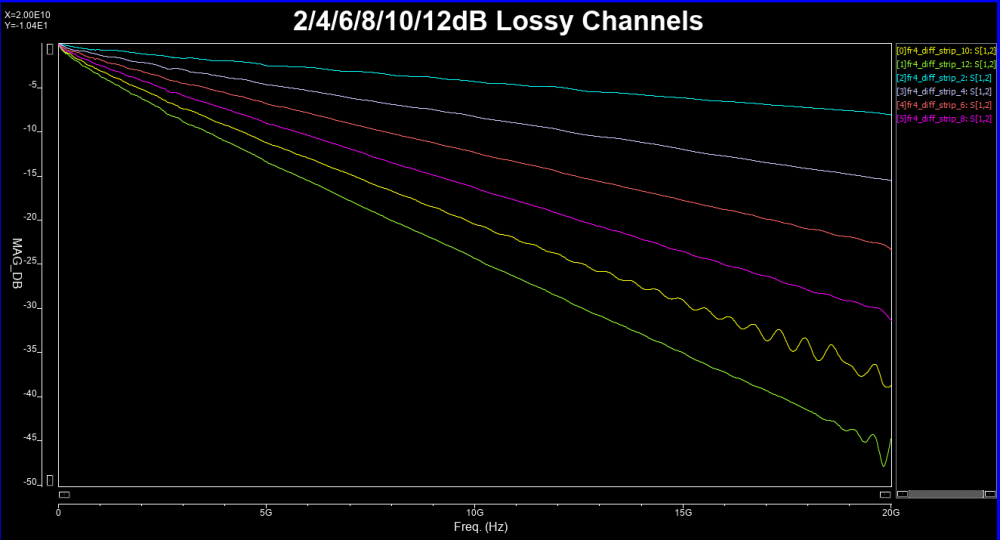
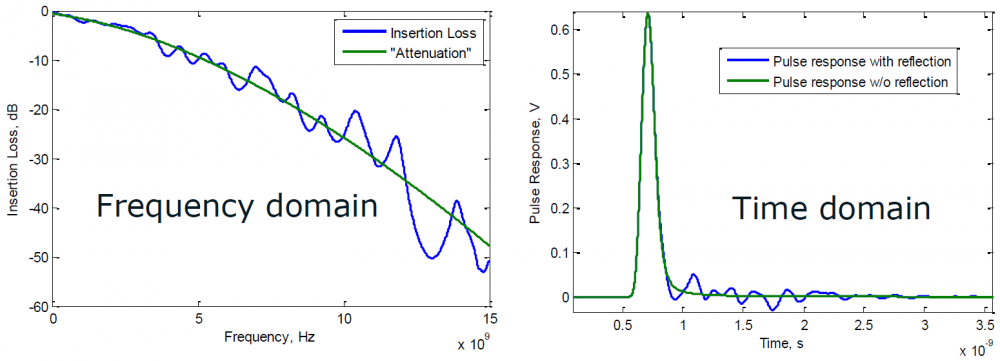

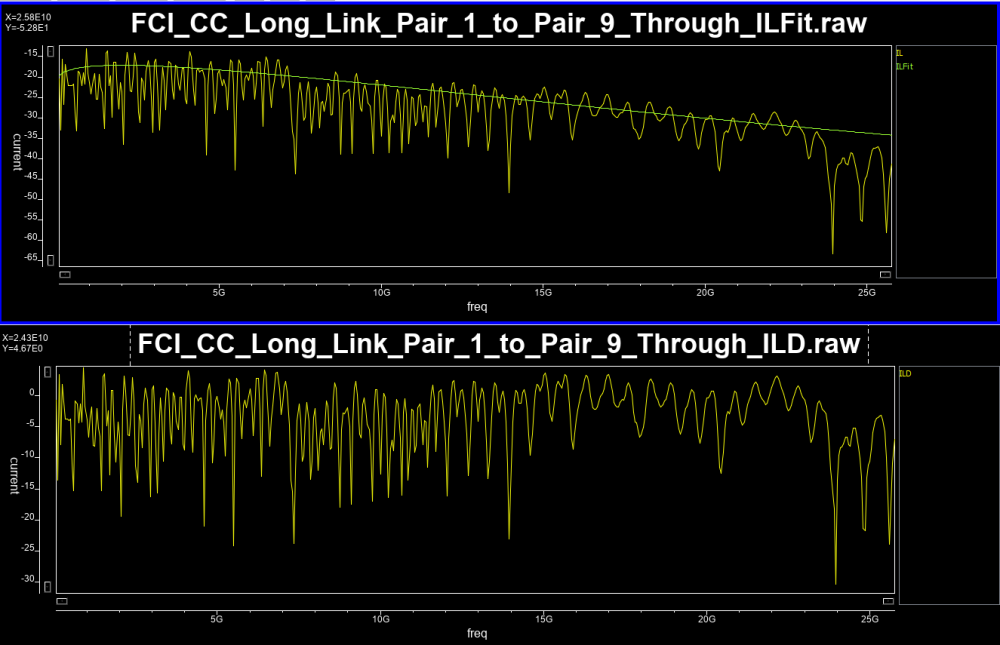
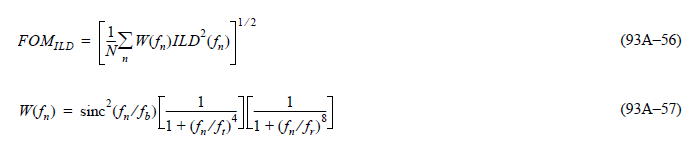


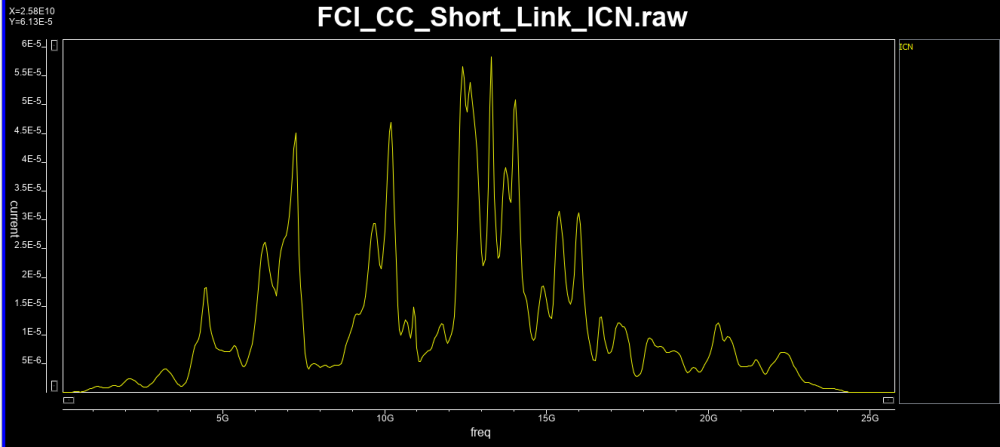

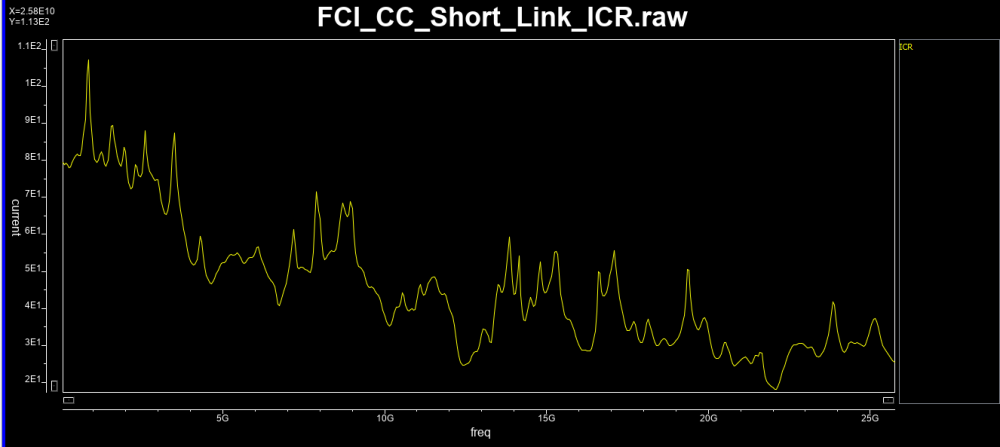
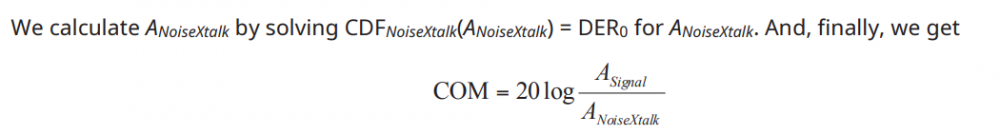

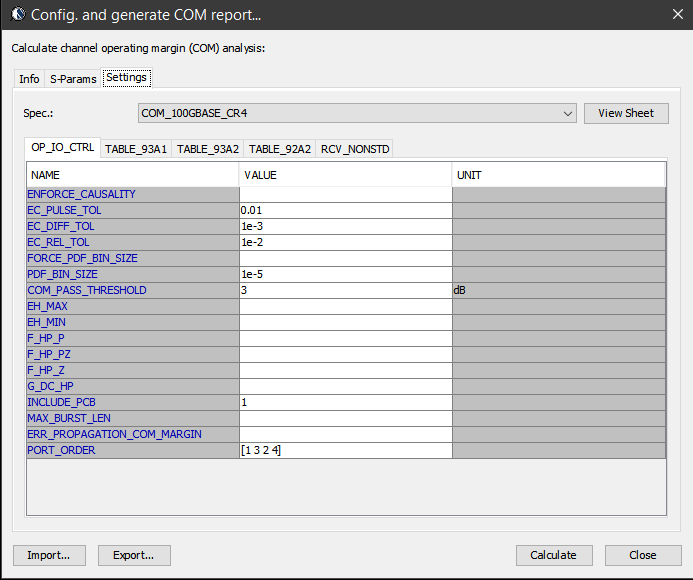
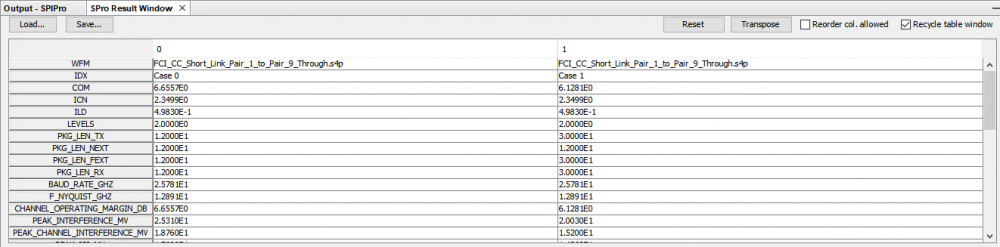
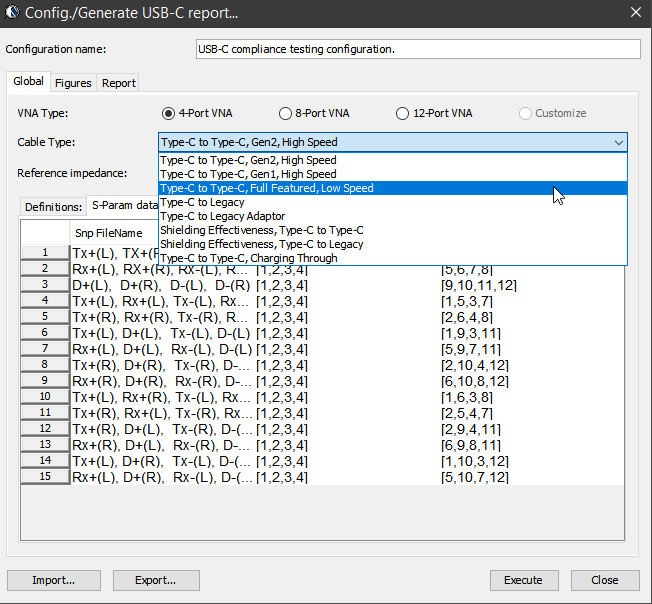
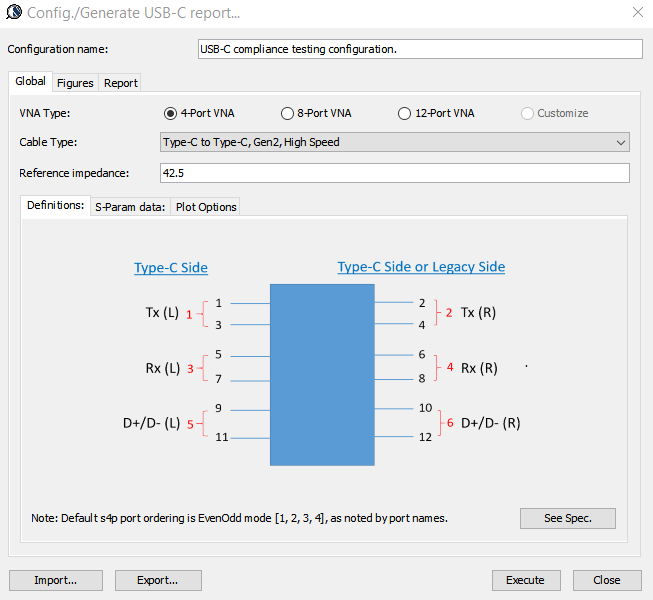


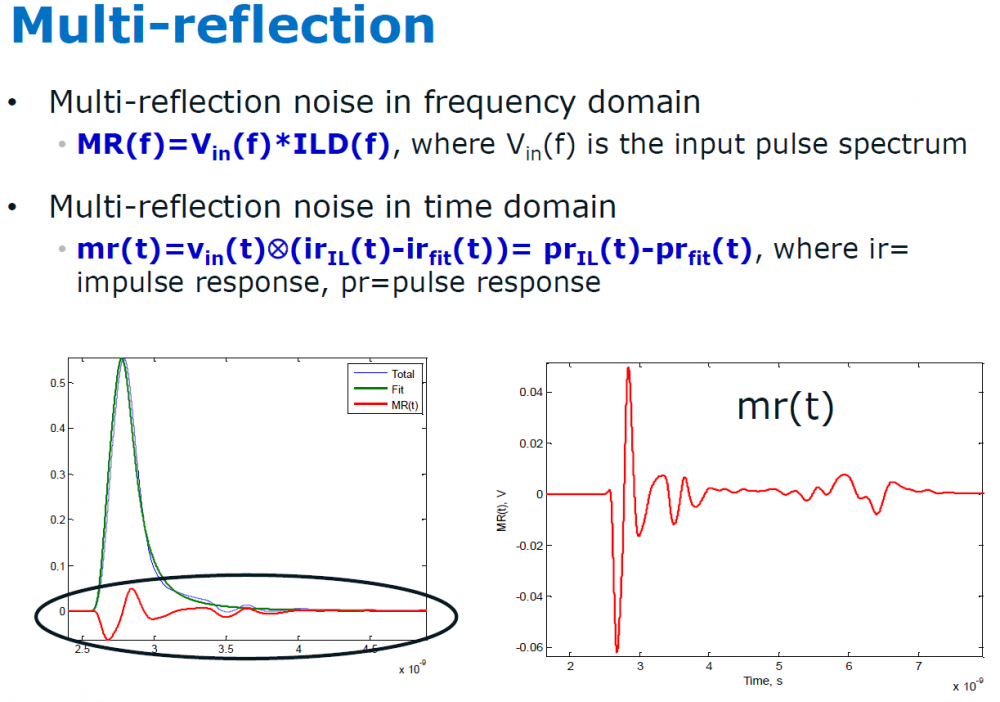



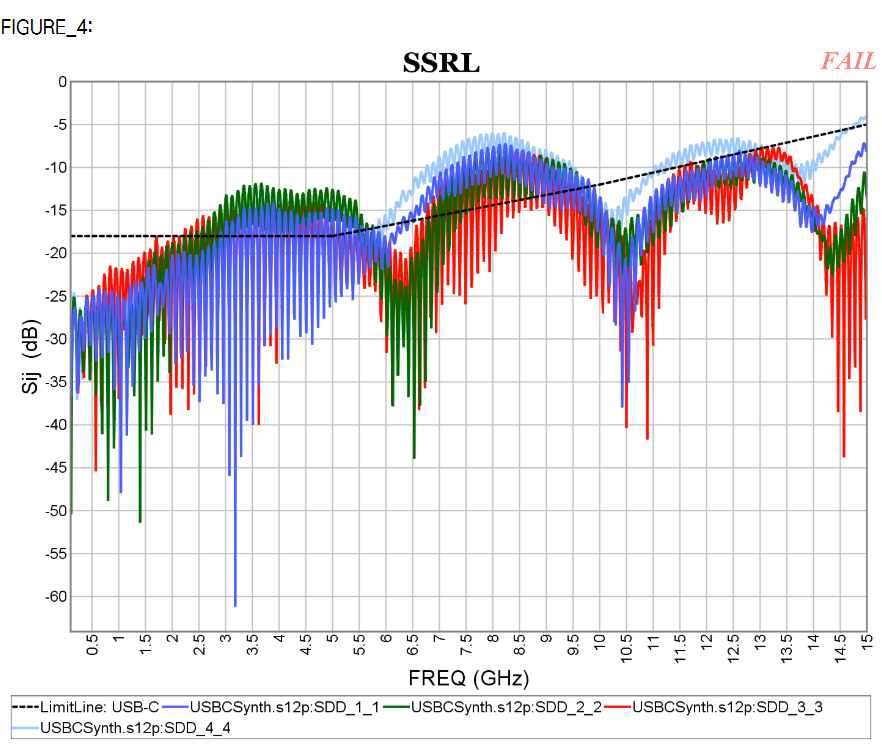
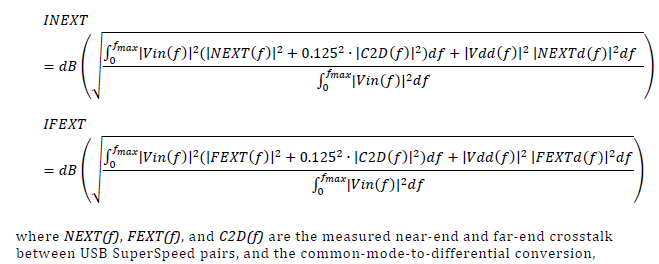
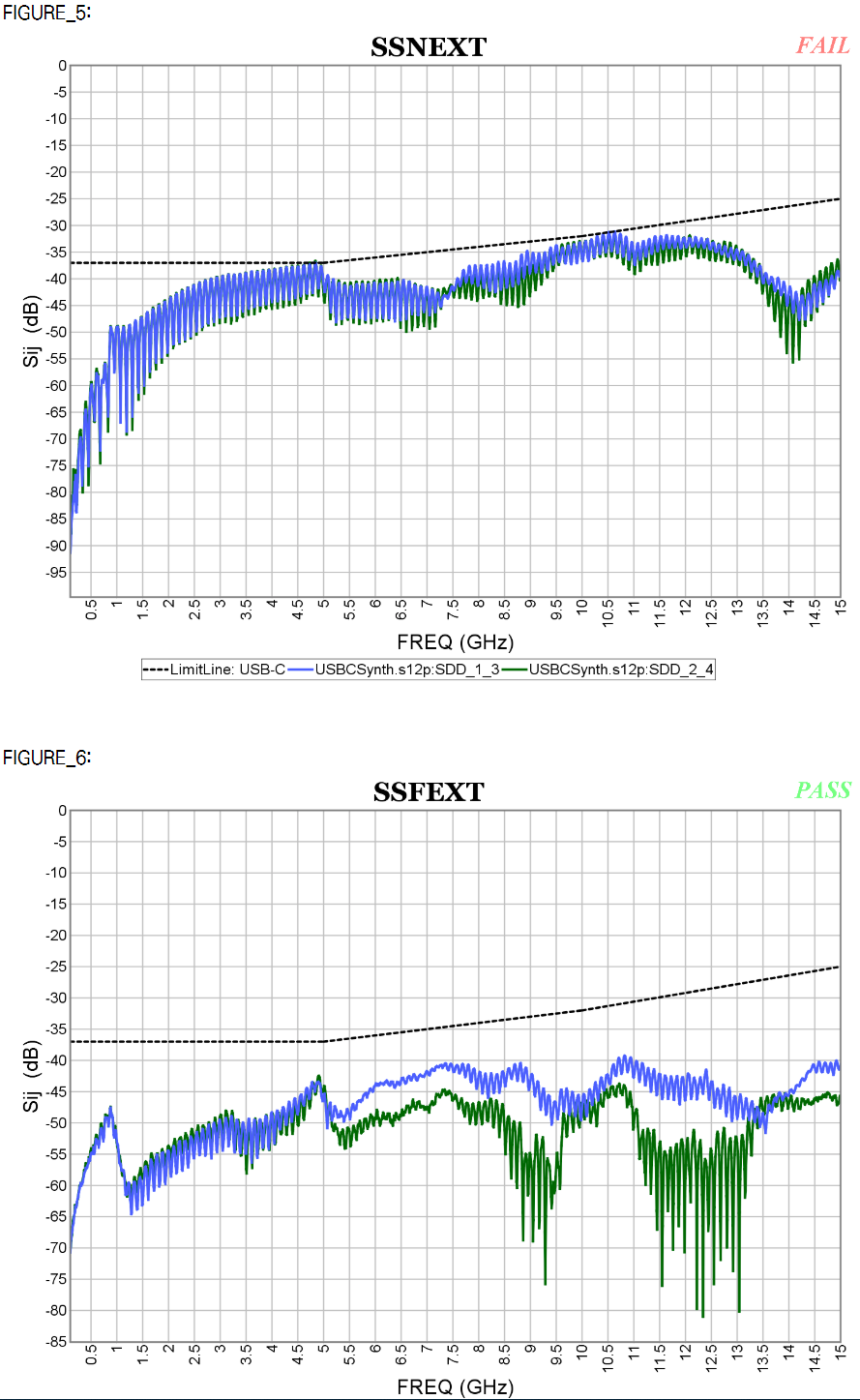


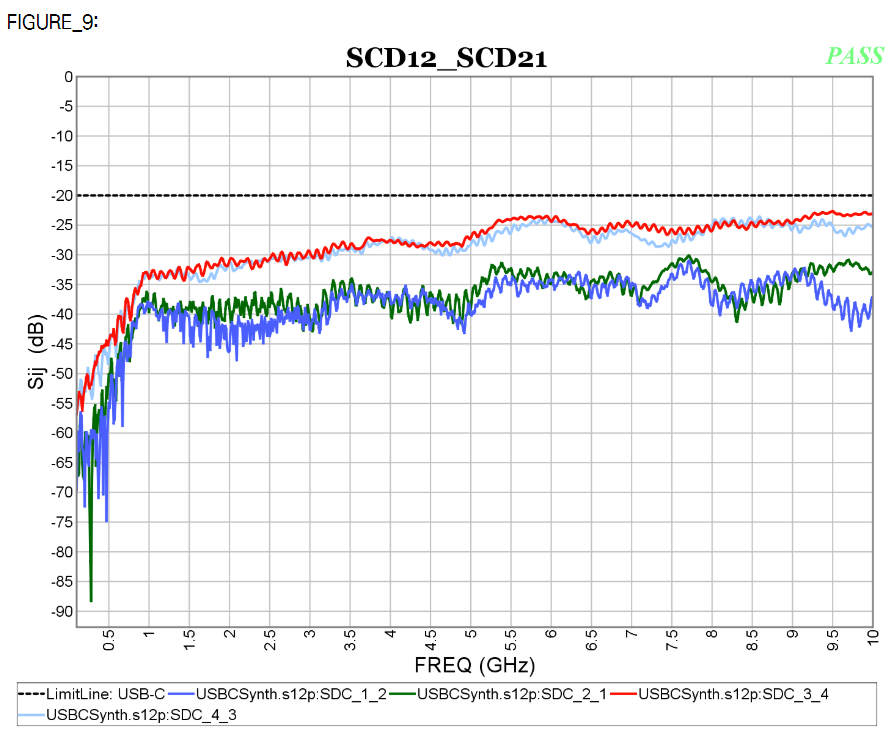

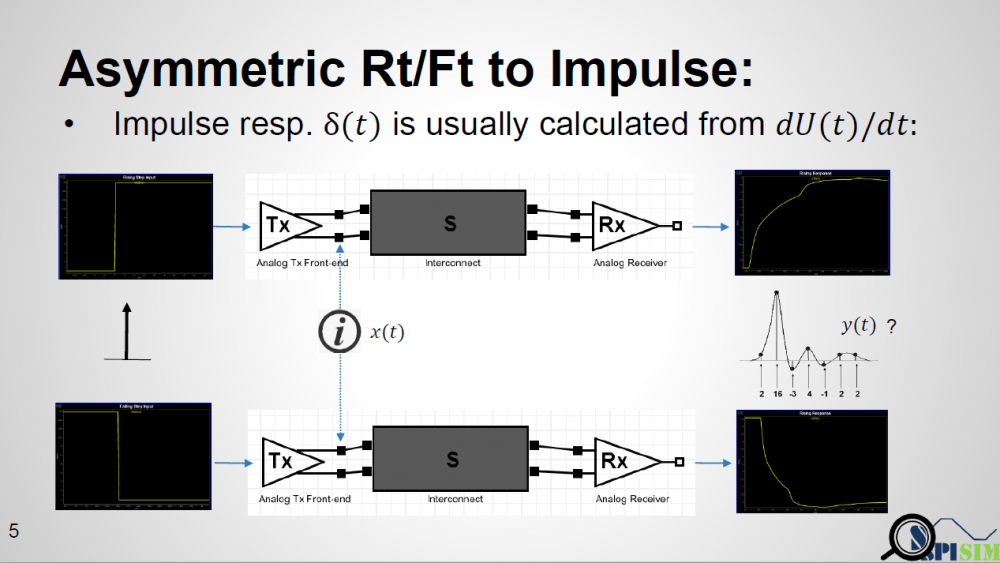
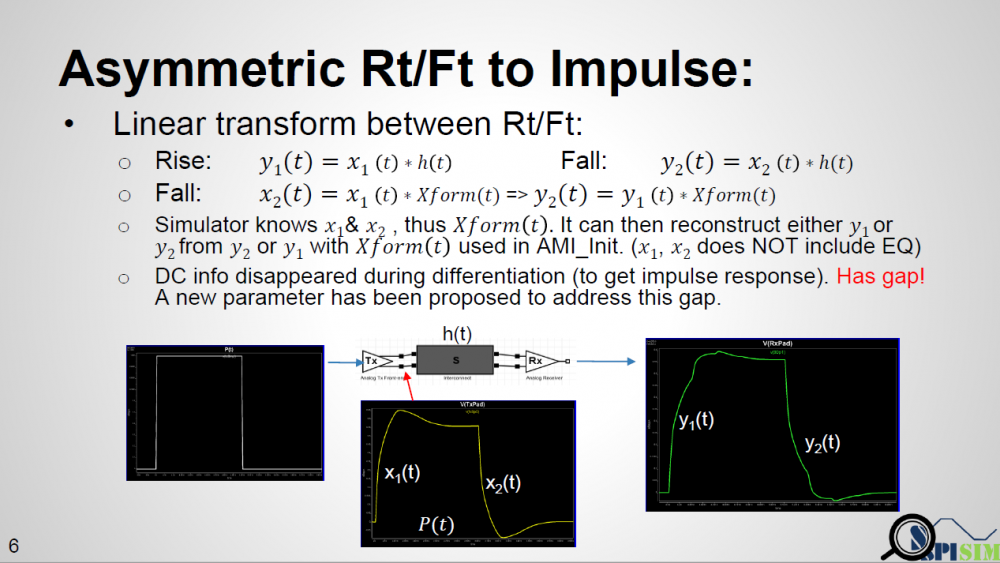




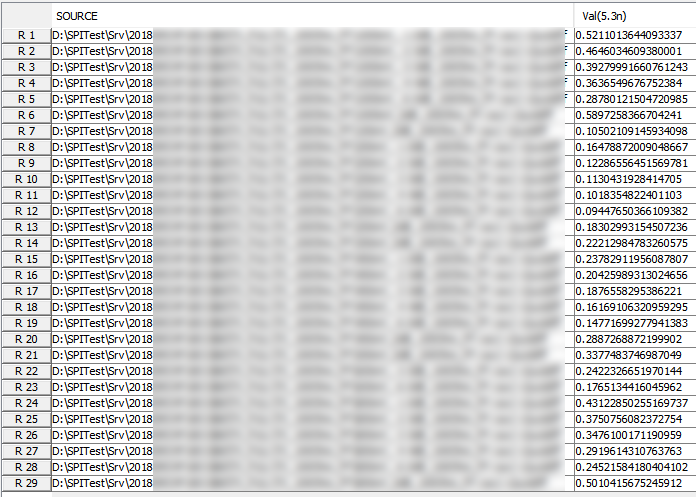 Similarly, data collected from measurement needs to be quantified. This may be done manually and maybe labor intensive as the noise is usually there:
Similarly, data collected from measurement needs to be quantified. This may be done manually and maybe labor intensive as the noise is usually there: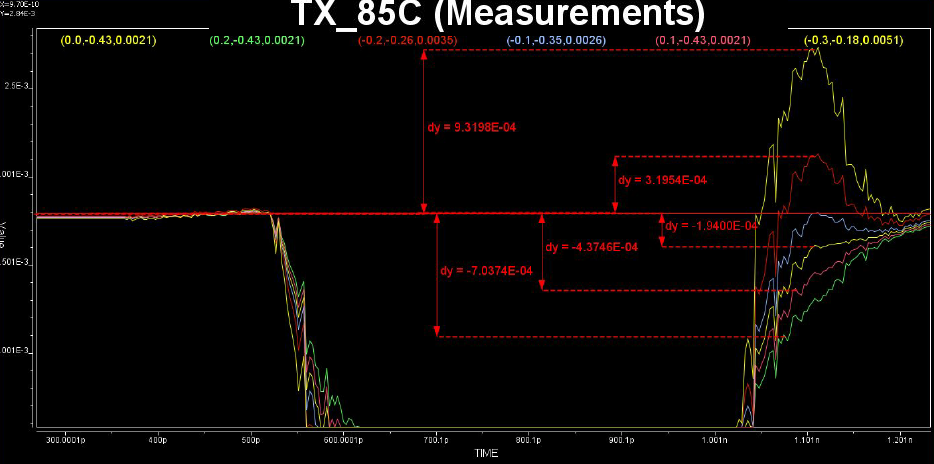
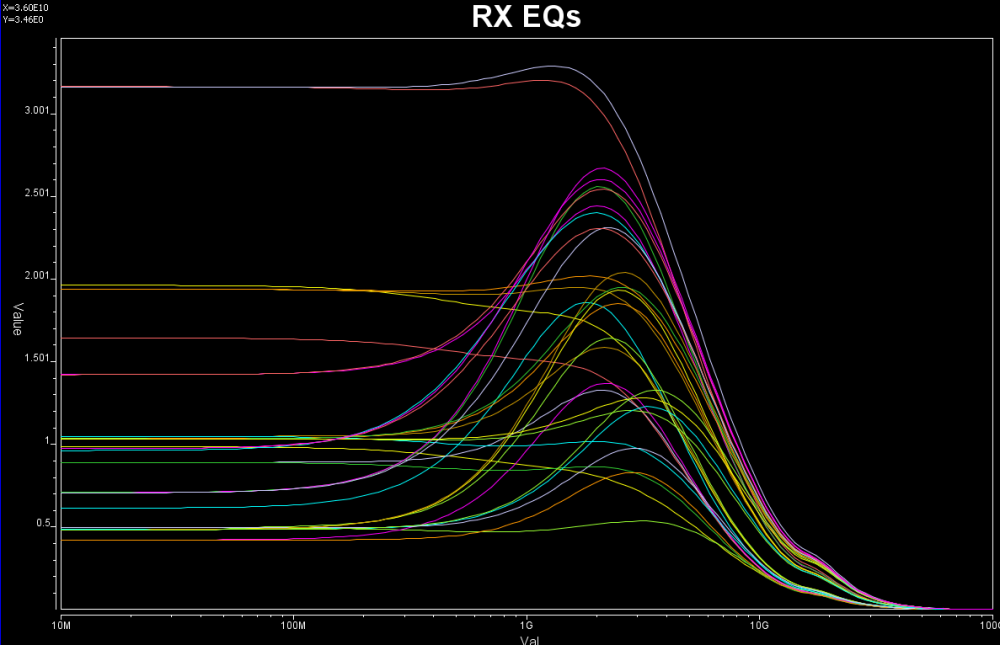
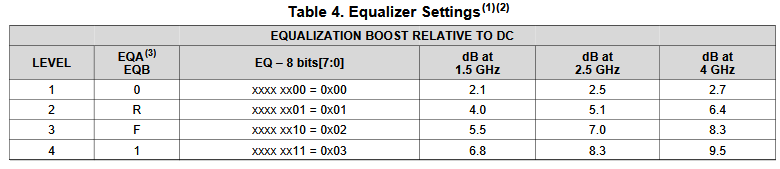
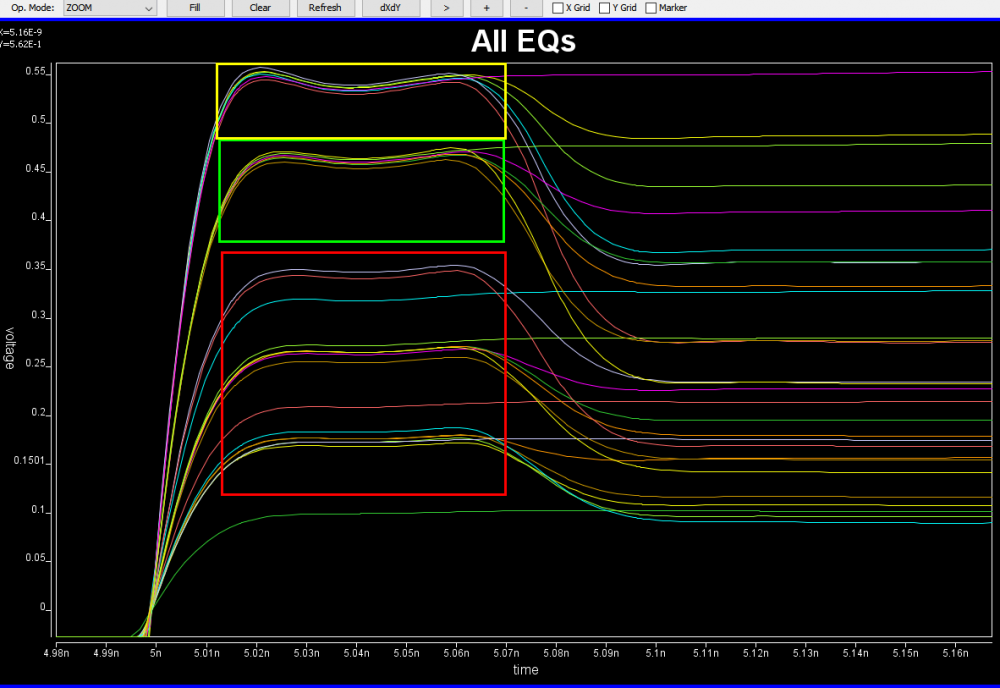
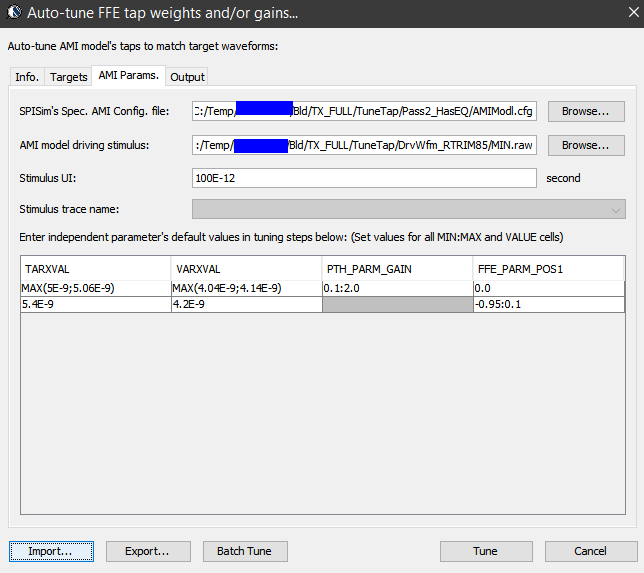

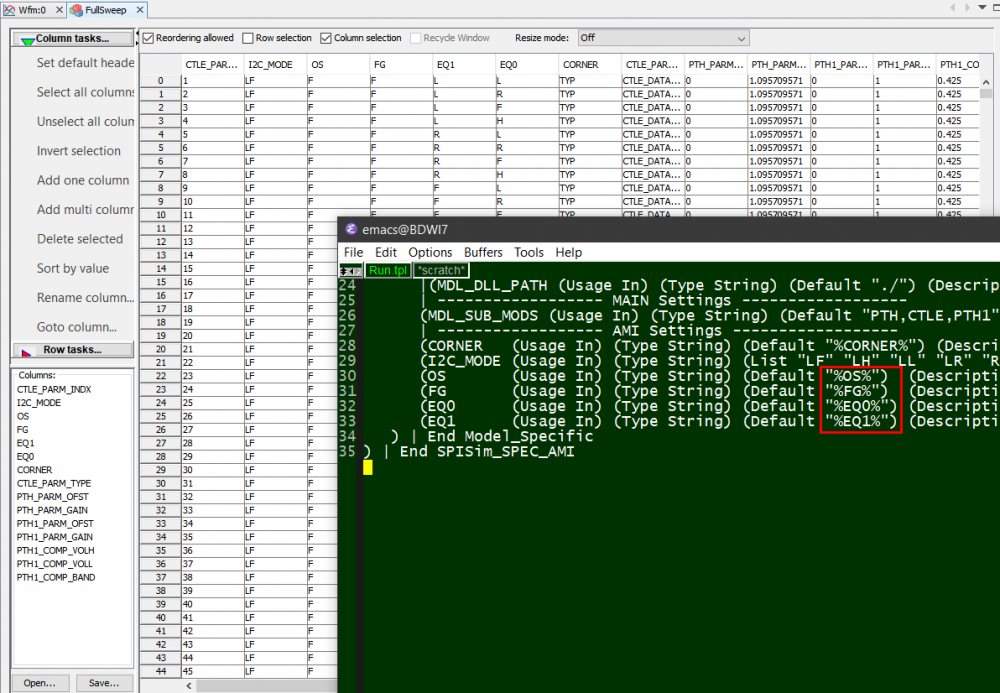
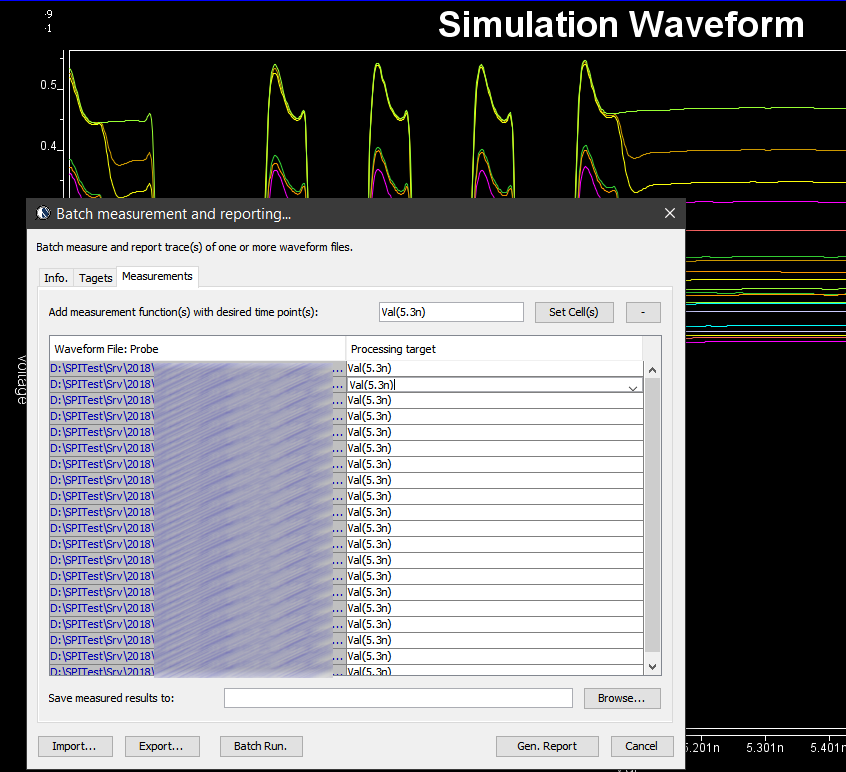
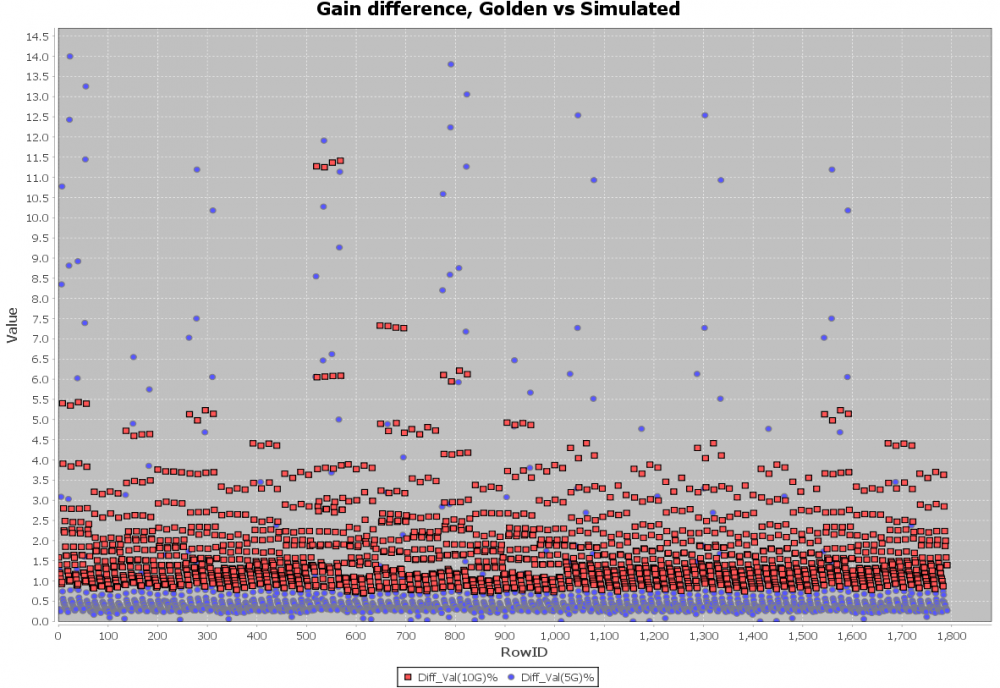
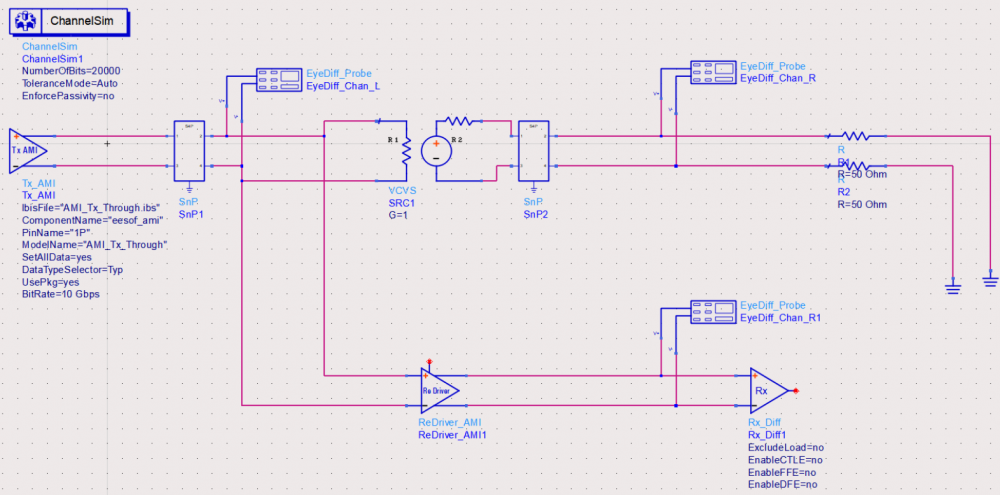

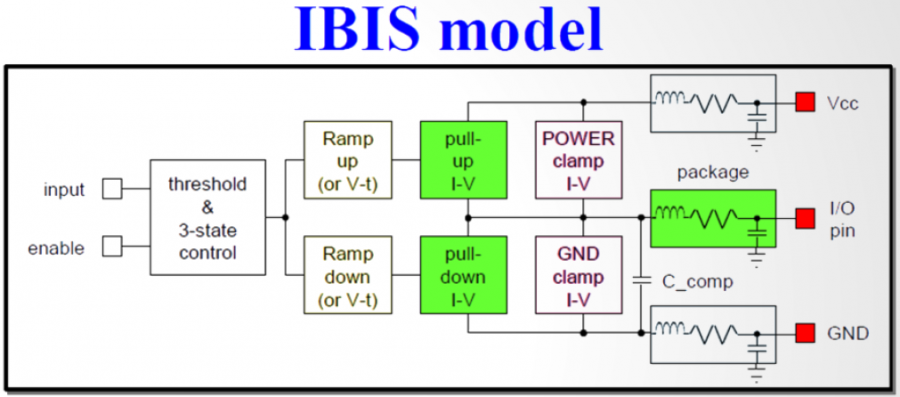
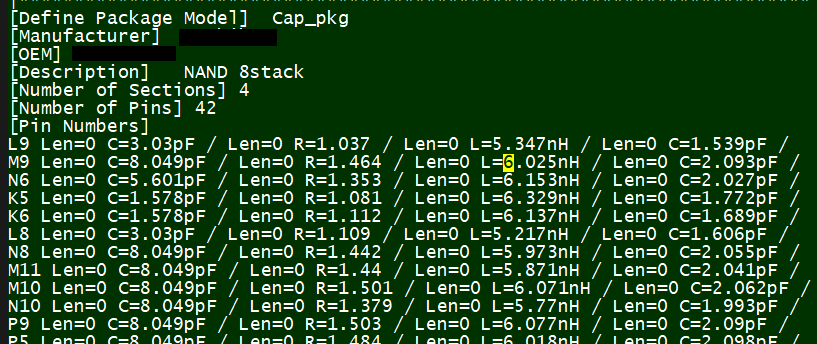
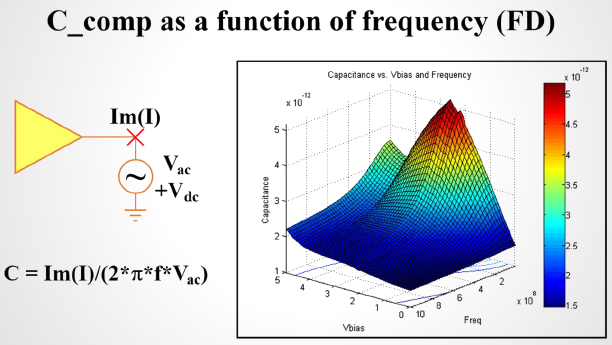

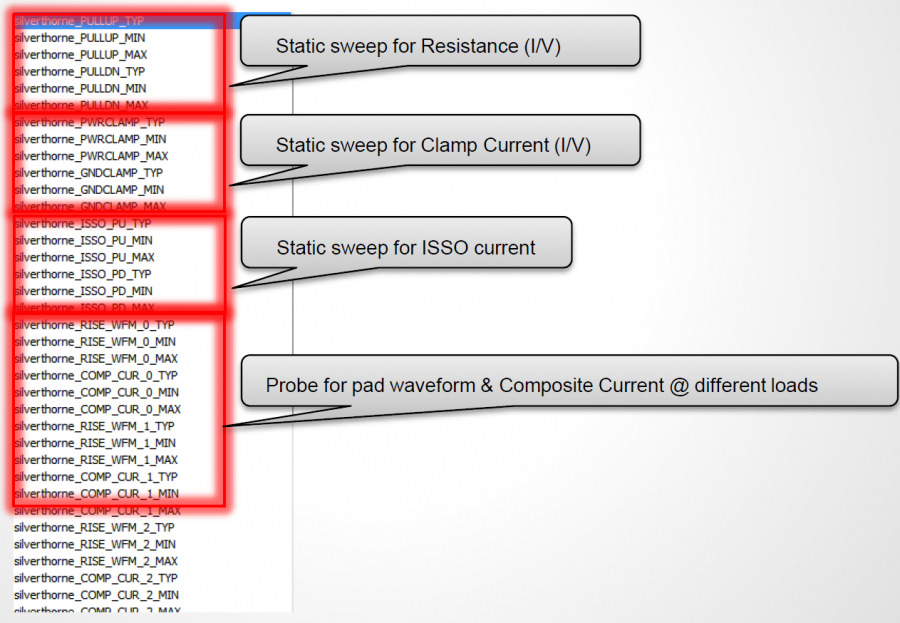
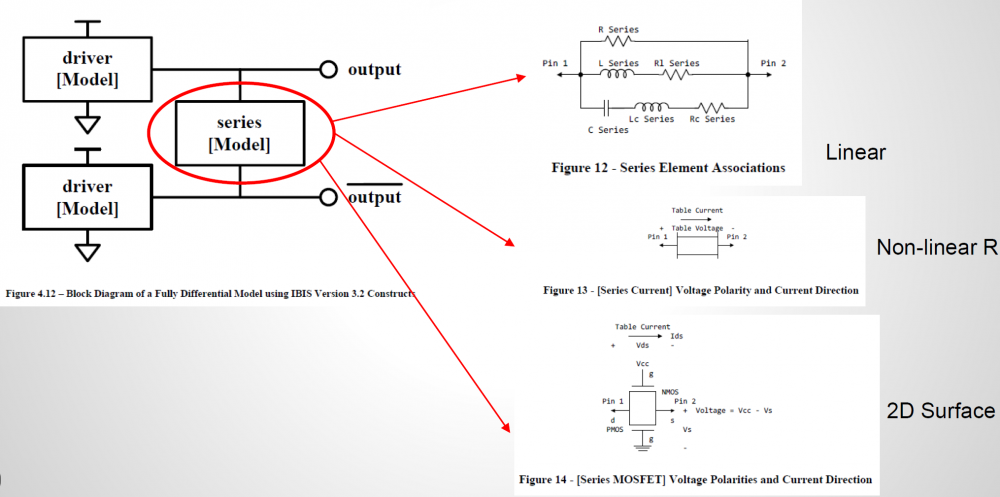
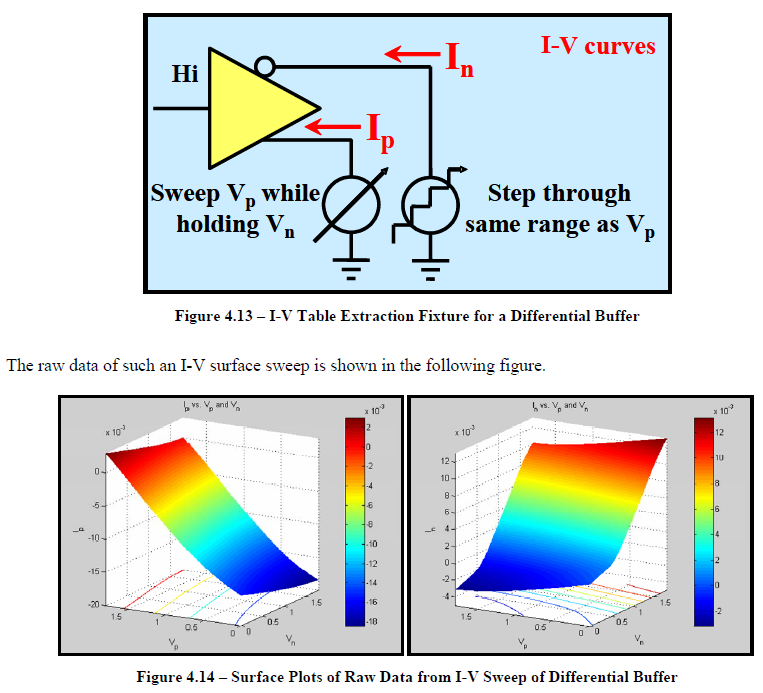
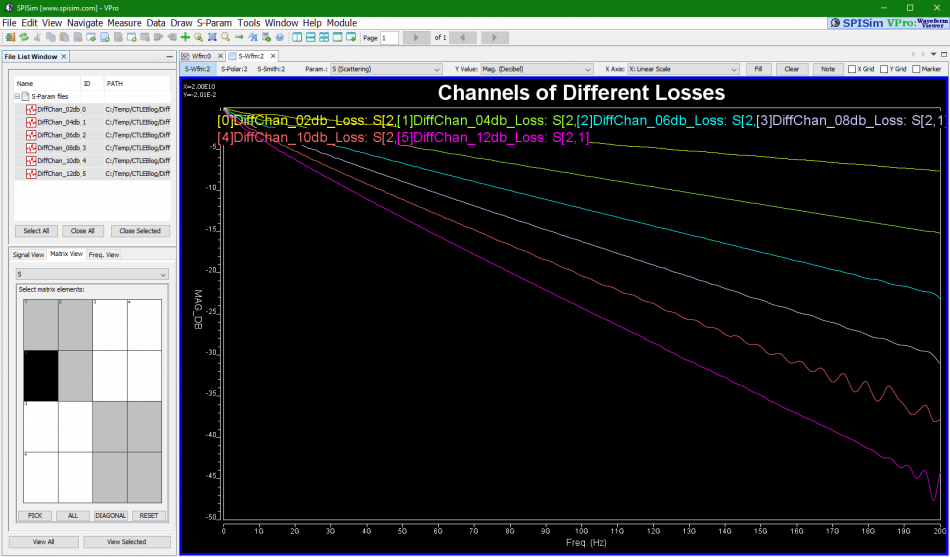

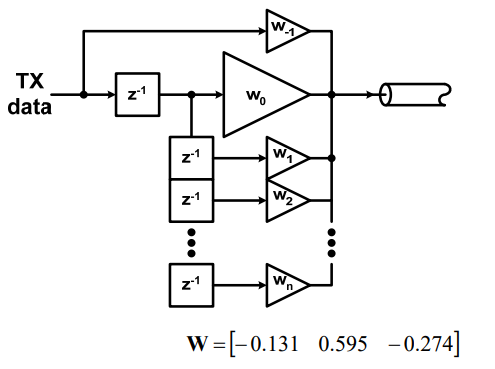
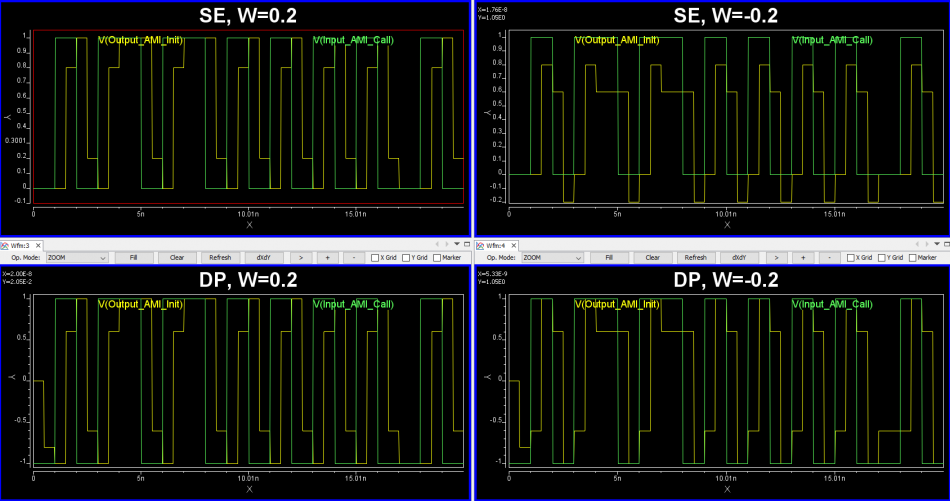
 So say if we are given a data sheet which has EQ level of some key frequencies like below:
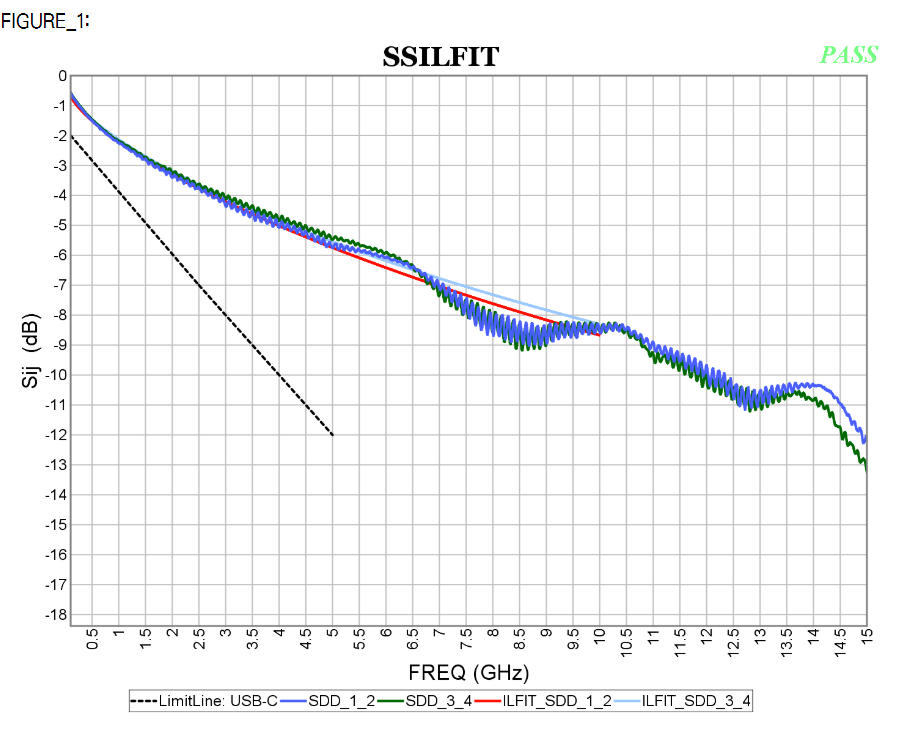
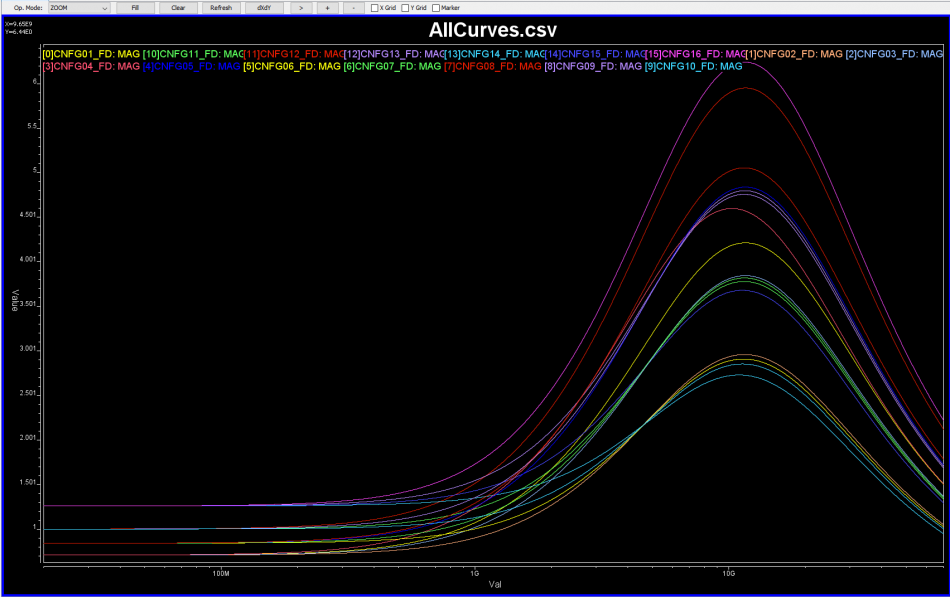
So say if we are given a data sheet which has EQ level of some key frequencies like below: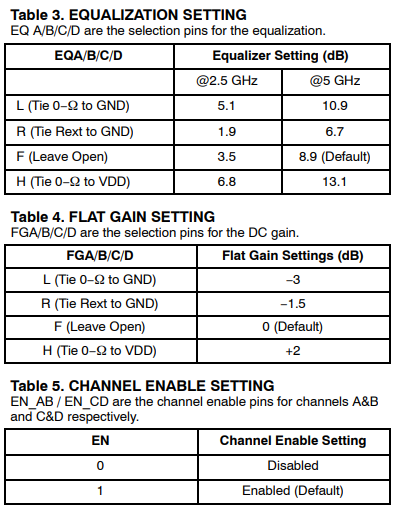 Then one can sweep different number and locations of poles and zeros to obtain matching curves to meet the spec.:
Then one can sweep different number and locations of poles and zeros to obtain matching curves to meet the spec.: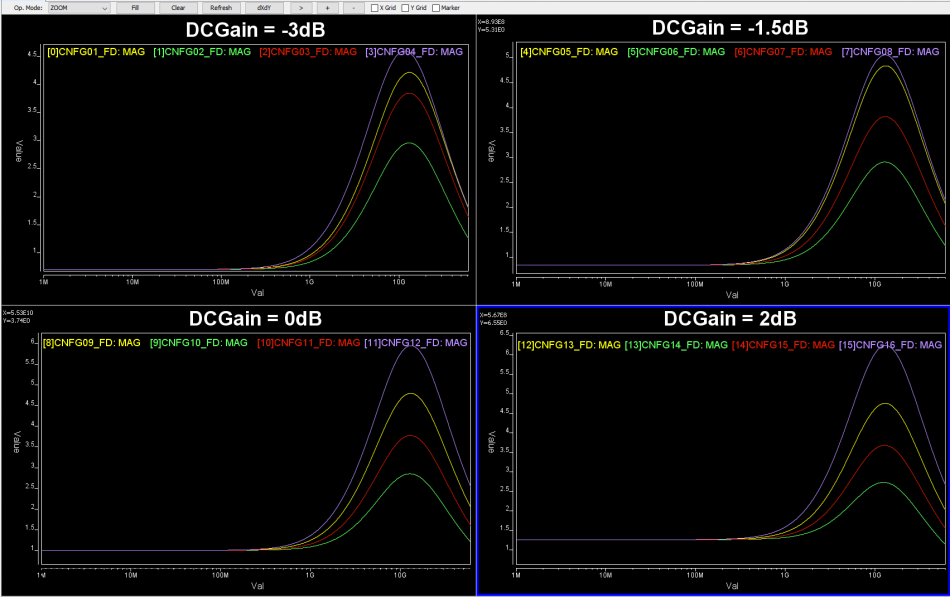 Such synthesized curves are well behaved in terms of passivity and causality etc, and can be extended to covered desired frequency bandwidth.
Such synthesized curves are well behaved in terms of passivity and causality etc, and can be extended to covered desired frequency bandwidth.