Tag Archives: simulation

IBIS-AMI: Study of DDR Asymmetric Rt/Ft in Existing IBIS-AMI Flow

Posted on by
Reply

[This blog post is written in preparation for the presentation of the same title to be given at the 2019 DesignCon IBIS Summit. Presentation slides and audio recording are linked at the bottom of this post.]

This paper is written by both Wei-hsing Huang (principle consultant at SPISim USA) and Wei-kai Shih, who is Tokyo based.

Motivation:

Here in US, one of IBIS committee’s working groups, IBIS-ATM (advanced technology modeling) has regular meeting on Tue. I try to call-in whenever possible to gain insights on upcoming modeling trends. During mid 2018, DDR5 related topics were brought up: Existing AMI reference flow described in the spec. focuses on differential or SERDES. For example, the stimulus waveform is from -0.5 to 0.5 and/or a single impulse response is used for analysis, thus assuming symmetric rise time (Rt) and fall time (Ft) mostly. Whether this reference flow can be applied to DDR, which may have asymmetric Rt/Ft and single-ended like DQ, is the center of discussion. Different EDA companies in this work group have different opinions. Some think the flow can be used directly with minimal change while others think the flow has fundamental shortcomings for DDR. Thing about IBIS spec. change is that whoever think the current version has deficiencies needs to write a “buffer issue resolution document (BIRD)”. Doing so will inevitably disclose some of the trade secrets or expose shortcoming of the the tool. As a result, while there are companies which think change may be needed, no flow change have been proposed at this point. As a model maker, I wonder then how existing flow can be applied to DDR without major change? Thus this study is to demonstrate “one” possible implementation. Existing EDA companies may have more sophisticated algorithms/implementations to support this asymmetric condition, but the existence of “one” such possible flow may convince model makers that it’s time to think about how DDR AMI may be implemented rather than waiting for the unlikely spec. change.

AMI_Init:

There are both “statistical” and “bit-by-bit” flows in channel analysis. In either case, the first step an EDA tool will do before calling AMI model is “channel calibration”. According to the spec. the impulse response of the channel, which includes analog buffer, is obtained here. For a SERDES design which has no asymmetric Rt/Ft issue, this impulse is then sent to TX AMI followed by RX AMI, resulting impulse response is then calculated using probability density function (PDF), integrated to be cumulative density function (CDF), then obtain bathtub plots etc.

The textbook definition of an impulse response is from a “delta response” input which happens at the infinite small time step. In real situation, there is no such thing as an “infinite small time step”. The minimal step used by a simulator is a “time step” which is usually 1ps or more. Buffer will not toggle from low to high back to low in a single time step. So in reality, simulator often uses step response then take derivative to get impulse response. Now the problem comes: for an analog channel with asymmetric Rt/Ft, these two step response (ignoring the sign) are different. That means we will have two different impulse response, then which one should be send to AMI models? A note here up front is that it’s EDA tool which sets up the calibration, so it has any nodal information, such as pad of Tx and Rx analog buffer, if needed.

Asymmetric Rt/Ft:

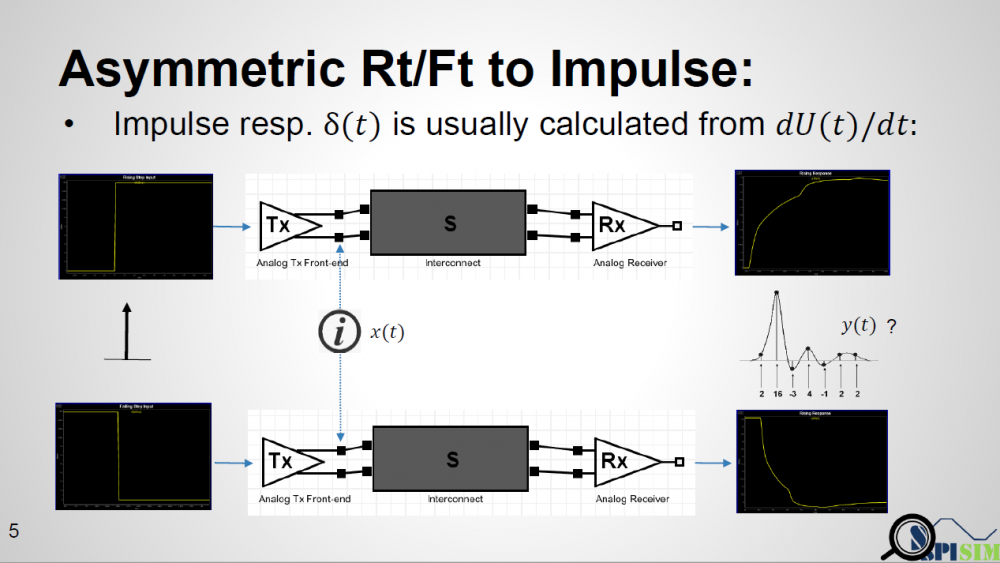
One may think that there is no such limitation that an AMI model can only be called once. So theoretically, a simulator can run analysis flow twice… impulse calculated from rising step response is used for the first time and the one from falling step response is used for the second time. However, not only is this not efficient, a model may not be implemented properly such that calling AMI_Init again right after AMI_Close may cause crash if it’s in the same process and model pointer was not released completely. Thus doing so may hamper a simulator’s robustness.

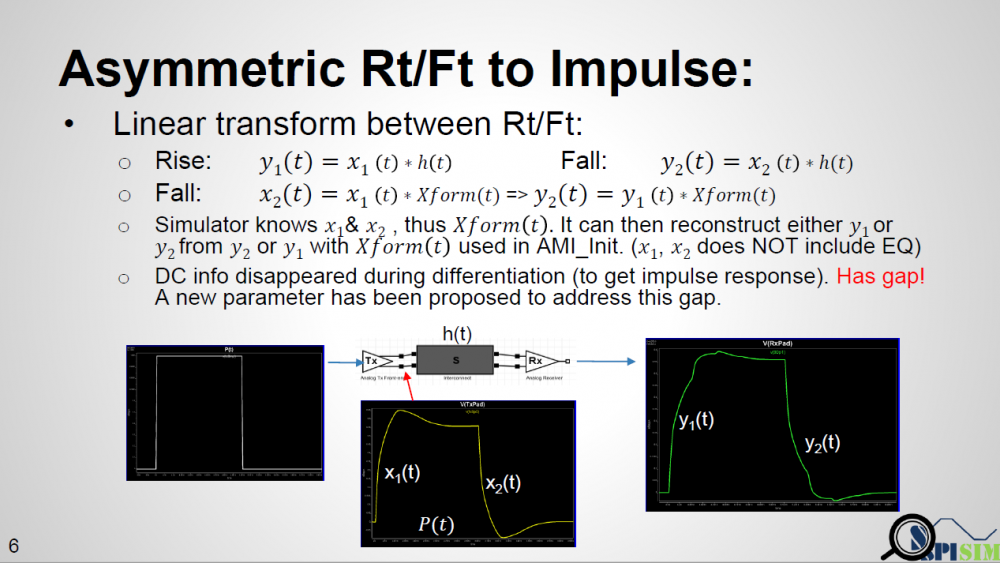
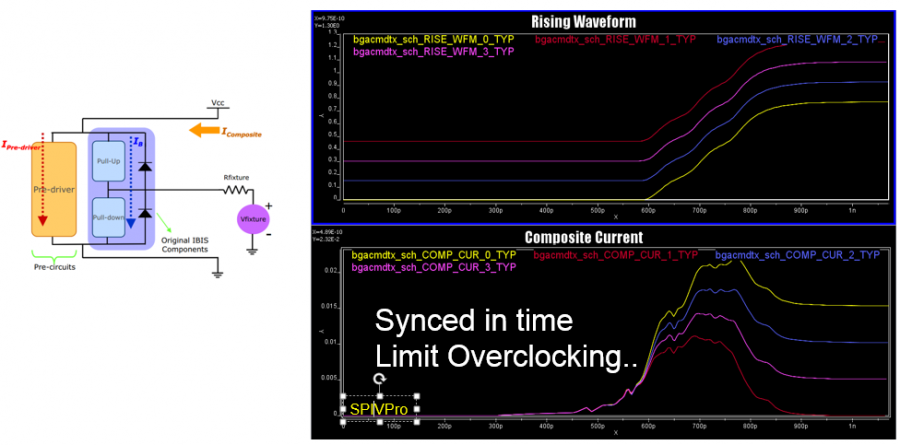
As depicted in the picture above… if a simulator uses a long UI pulse to calibrate the channel, then both rising and falling step response are included in one simulation. Now let the data captured at Tx analog pad as X1 and X2 for rising and falling portion respectively, the data captured at Rx analog pad Y1 and Y2 will be X1 and X2 convolved with interconnect’s transfer function, which is LTI. If we derive a Xform(t) which is transfer function between X1 and X2, then that Xform(t) should also be able to transform between Y1 and Y2.  That means if a simulator can calculate Xform(t) it self, then regardless the impulse response it sent to AMI models is calculated from rising or falling step response, it can always “reconstruct” the result from the other type of impulse response using this Xform(t) function.

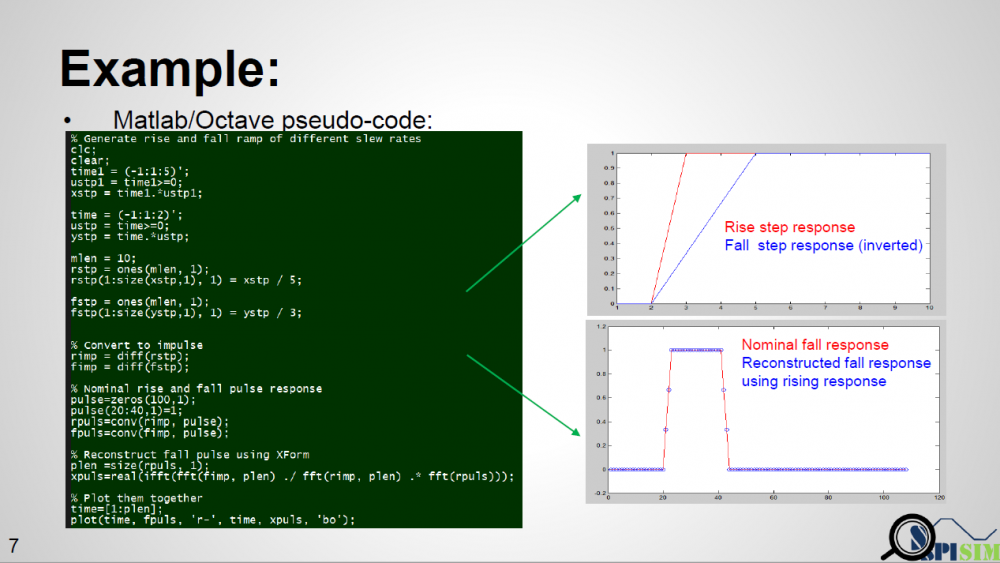
To prove this concept, we have written a simple matlab script taking step inputs of different slew rate, say inp1 and inp2. It calculates the Xform(t) function from both inputs and then reconstruct the response out2′ from out1. When overlaying nominal output out2 and reconstructed out2′ together, we can see that they match very well, thus prove the concept.

Once we have response from both different slew rates, we can construct their respective eyes then use each one’s different portion to construct a synthesized eye. Such eye will not be symmetric like that calculated from SERDES.

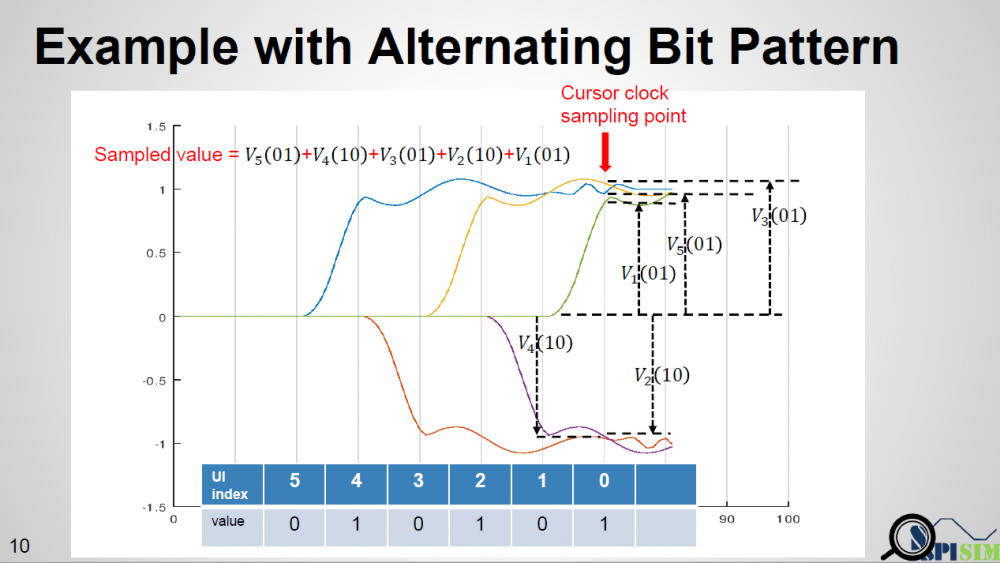
When calculating PDF for asymmetric case, one may also need to consider the precedent bit’s value and use a tree like structure to keep track of possible bit sequence. For example, for a typical SERDES bit sequence, if encoding is not considered, each bit will have 50% one and 50% zero. PDF is constructed based on that assumption. But in an asymmetric case, if the data used at the cursor is from rising response, then the cursor bit must be 1 while (cursor – 1) must be zero. If (cursor – 2) is 1 again, then the tail of falling response at (cursor – 1) will be superimposed to the cursor data. That is, we can’t treat each bit to have same 50% probability when constructing PDF. It’s not a binomial distribution as each occurrence is not independent. A simulator may need to determine the maximum bit length to keep track of first, then based on that depth to form tree-like sequence which leads to the rising or falling steps at the cursor location. Finally use superimpose to construct the overall response.

AMI_GetWave:

According to the reference flow for the bit-by-bit case: equalized Tx output from digital bit sequence is converted with channel’s impulse response. The resulting waveform is then sent to Rx EQ before getting final results. Either Tx EQ or Rx EQ or both may not be LTI so usage of aforementioned Xform(t) is not applicable.

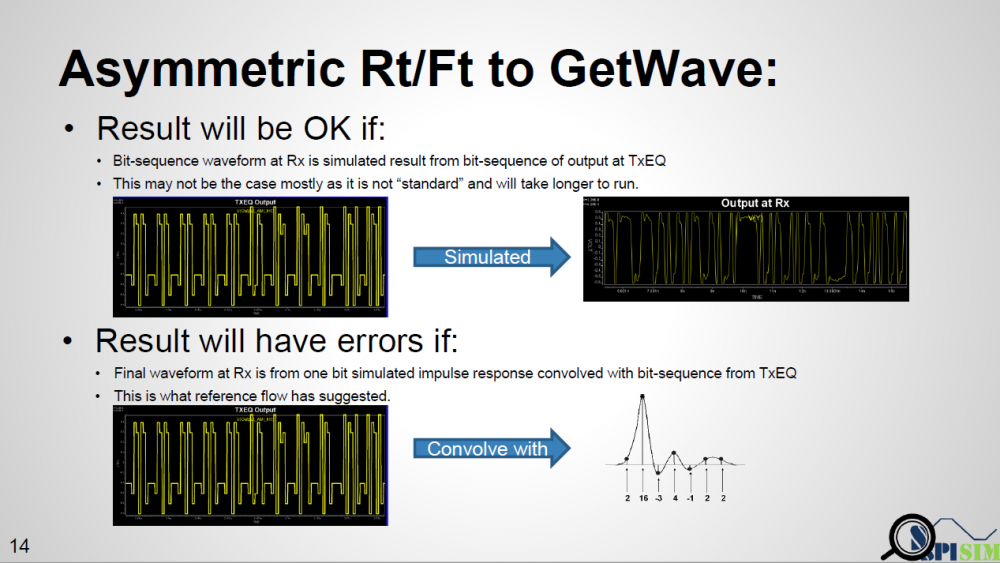
As a fruit of thought… the spec. only mentions that in a bit-by-bit mode, the output of Tx AMI model is equalized digital sequence, while input to the Rx EQ must be the channel response from that sequence, then are there other ways to get such response to Rx yet with different Rt/Ft considered?

One example is like shown in top half of the picture above. If a simulator takes that equalized digital input and “simulate” to get final response, then this “simulation process” should have taken different Rt/Ft into account and has valid results. However, this process will be slow and I don’t think any simulator is doing it this way. Furthermore, the spec. specifically say it needs to “convolve” with impulse response. First of all, this impulse can be from rising or falling. Secondly, even we decide to decovolve with input first (thus has sequences of different delta response) then convolve with pulse response (i.e. one simulated UI), will there be any issue?

From the plot above…  we can see that when a pulse has different rising and falling slew rate, using superimpose to construct 011… will find “glitches” at the trailing high state portion. The severity of this “glitches” depends on how much difference the Rt/Ft is. So using a pulse response here will still not work.

A simple matlab script has also been written to demonstrate occurrence of such “glitches”. This proves that not only using an impulse response to convolve with Tx EQ’s output is problematic, even using a full simulated pulse (which has asymmetric Rt/Ft’s effect) to convolve delta sequences (this delta sequence is original TX EQ’s output deconvolve with one digital bit) will still be problematic. Glitches will happen for consecutive ones or zeros due to the mismatches of Rt and Ft. Thus one must use rise step and fall step response instead when doing such kind of convolution.

Summary:

In this presentation, we discussed how existing AMI flow may be applied to asymmetric Rt/Ft such as those often seen in DDR case. A “smarter” EDA tool should be able to handle this situation without changing on spec.’s reference flow. When a channel analysis is performed in a “statistical” flow, an EDA tool can obtain waveform data at both Tx and Rx analog buffer’s pads during calibration process. Such data can be used to construct a transform function, XForm(t). With this function, impulse response through EQ can be reconstructed and thus built an asymmetric eye. Tree structure may be needed to keep track of possible bit combinations. In a “bit-by-bit” flow, the current spec. may be too specific as it forces to use convolution of TX EQ’s output with channel’s impulse response before sending to RX EQ. Such direct convolution may be problematic. A “smarter” simulator may calculate it using different method without changing data output from TX EQ and input to the RX EQ. Step response should be used as different Rt/Ft will cause “glitches” when consecutive ones/zeros are present if convolution method is used.

Links:

Presentation: [HERE] (http://www.spisim.com/support/paperetc/20180202_DesignConSummit_SPISim.pdf)

Audio recording (English): [HERE]

IBIS model: How does IBIS work

Posted on by
5

* Buffer model: What is in an IBIS model:

IBISType

IBIS Spec defines many different buffer model types, as shown above. Different model types requires different modeling data to be included in the IBIS model section. In general, an IBIS model will have the following info.

  • Operational conditions: such as voltage and temperature range for operations
  • Parasitics/Loading conditions: such as C_Comp of the model. This value does not impact buffer performance when output is well terminated.
  • I/V table: These are I vs V tables of different corners for pull-up (PU), pull-down (PD), power clamp (PC) and ground clmap (GC) circuitry. They are general representations of non-linear resistor like those E elements used in the hspice circuit. According to the spec, the sweep range for these table should be from -Vcc to 2Vcc where Vcc is the power supply voltage. The reason is that in case of total reflection from the far side of the loss-less channel, either to do fully open or fully connected to ground, added full Vcc voltage swing will extend the original 0 ~ Vcc range to -Vcc to 2Vcc. Also notice that for IV sweep of pull-up circuitry, i.e. PU and PC, the voltage is Vcc relative. That means value of I when V = 0 is actually when V = 0 to Vcc = Vcc to ground. One usually needs to make such conversion back to be VSS relative during debugging process. SPISim’s IBIS module, SPIBPro, has such a GUI button to translate Vcc relative to Vss relative waveform directly.
    IBISPUPD
    IBISPCGC
  • ISSO PU/PD: These are current tables introduced in V5.0, used when terminal VCC and VSS voltages are not ideal. With lower VCC voltage due to PDN network (i.e. voltage droop), buffer strength will become weaker. So are those caused by ground bounce. This phenomena is usually called “Gate modulation effect”. ISSO/PU and PD data defines the effective current of the pull-up/pull-down structures as a function of the voltage on the pull-up/pull-down reference nodes (ideal is Vcc and Vss/Gnd)
  • V/T table: These are tables representing buffer’s voltage at die output vs elapsed buffer switching time. Under different loading condition, such as test load and test fixture, resulting waveform will be different. An ibis model usually will include at least two such VT tables under different loading condition to provide sufficient coverage during real world operations.
    IBISVT
  • I/T table: These are tables representing buffer’s drawing current vs elapsed buffer switching time. It needs to be synchronized with aforementioned VT table so that current drawn happens at the exactly same time point for the same test fixture. This current is usually composed of bypass current, pre-driver current crow-bar current and termination current if present.
    IBISIT

* How is IBIS modeling data used during circuit simulation:
With so many tables, one may wonder how they are used in a circuit simulator. To simplify, let’s first remove the ESD protection circuitry PC and GC as they are usually reversed biased and contribute very small amount of current. For the remain PU and PD circuitry, we can imagine them as non-linear resistors, similar to those MOSFET’s channel resistance when terminal voltages varies. How these two table work together during different loading condition decide the resulting transient VT waveform shown in the VT/IT table.
IBISKuKd0

During rising transition, PU circuitry gradually turns to fully ON while PD circuit gradually turns to fully OFF. Similarly, during falling transition, PU gradually turns to fully OFF and PD turns ON. Thus we can define a time dependent parameter, “switching coefficient”, which will be applied to PU and PD separately such that the resulting current from these two branches mimic the gradually turning ON/OFF effect.
IBISKuKd1

Let’s call these two switching parameters Ku(t) and Kd(t). We needs two equations to solve these two unknowns. Now assuming we have to such VT table under different loading condition. At each time point of these two tables, we know the loading condition and instant output voltage of the buffer. Using these, we can solve Ku(t) and Kd(t) in which the time, t, is buffer switched elapsed time. That is, the x-axis of the VT table.

If we don’t have two waveform table, one may make an assumption that Ku(t) + Kd(t) = 1 at all times. This is usually true at the static high or static low output condition but may not be in between. One may also use ramp parameters in the IBIS model to generate an artificial VT table for the same purpose.
IBISKuKd2

For an IBIS model developer for circuit simulator, he/she needs to consider all the branch current to obtain accurate Ku(t), Kd(t) solutions. So reverse bias current from ESD circuit need to be put in and so is the current flowing through C_Comp. For example, i=C_Comp * dV/dt can be sued to subtract current flow through this capacitor from the total output current and avoid double counting.

IBISCComp

For power-aware model, another level of scaling parameter needs to be applied. These new parameter need to scale the buffer output strength based on the instant nodal voltages across buffer terminals such that gate modulation effect will be taken into account.

Interested reader may find detailed algorithm in the following two paper.