Note:
- Dataset and ipython notebook of this post is available at SPISim’s github page: [HERE]
- This notebook may be better rendered by nbviewer and can be viewed [HERE].


[This blog post is written in preparation for the presentation of the same title to be given at the 2019 DesignCon IBIS Summit. Presentation slides and audio recording are linked at the bottom of this post.]
This paper is written by both Wei-hsing Huang (principle consultant at SPISim USA) and Wei-kai Shih, who is Tokyo based.
Here in US, one of IBIS committee’s working groups, IBIS-ATM (advanced technology modeling) has regular meeting on Tue. I try to call-in whenever possible to gain insights on upcoming modeling trends. During mid 2018, DDR5 related topics were brought up: Existing AMI reference flow described in the spec. focuses on differential or SERDES. For example, the stimulus waveform is from -0.5 to 0.5 and/or a single impulse response is used for analysis, thus assuming symmetric rise time (Rt) and fall time (Ft) mostly. Whether this reference flow can be applied to DDR, which may have asymmetric Rt/Ft and single-ended like DQ, is the center of discussion. Different EDA companies in this work group have different opinions. Some think the flow can be used directly with minimal change while others think the flow has fundamental shortcomings for DDR. Thing about IBIS spec. change is that whoever think the current version has deficiencies needs to write a “buffer issue resolution document (BIRD)”. Doing so will inevitably disclose some of the trade secrets or expose shortcoming of the the tool. As a result, while there are companies which think change may be needed, no flow change have been proposed at this point. As a model maker, I wonder then how existing flow can be applied to DDR without major change? Thus this study is to demonstrate “one” possible implementation. Existing EDA companies may have more sophisticated algorithms/implementations to support this asymmetric condition, but the existence of “one” such possible flow may convince model makers that it’s time to think about how DDR AMI may be implemented rather than waiting for the unlikely spec. change.
There are both “statistical” and “bit-by-bit” flows in channel analysis. In either case, the first step an EDA tool will do before calling AMI model is “channel calibration”. According to the spec. the impulse response of the channel, which includes analog buffer, is obtained here. For a SERDES design which has no asymmetric Rt/Ft issue, this impulse is then sent to TX AMI followed by RX AMI, resulting impulse response is then calculated using probability density function (PDF), integrated to be cumulative density function (CDF), then obtain bathtub plots etc.

The textbook definition of an impulse response is from a “delta response” input which happens at the infinite small time step. In real situation, there is no such thing as an “infinite small time step”. The minimal step used by a simulator is a “time step” which is usually 1ps or more. Buffer will not toggle from low to high back to low in a single time step. So in reality, simulator often uses step response then take derivative to get impulse response. Now the problem comes: for an analog channel with asymmetric Rt/Ft, these two step response (ignoring the sign) are different. That means we will have two different impulse response, then which one should be send to AMI models? A note here up front is that it’s EDA tool which sets up the calibration, so it has any nodal information, such as pad of Tx and Rx analog buffer, if needed.
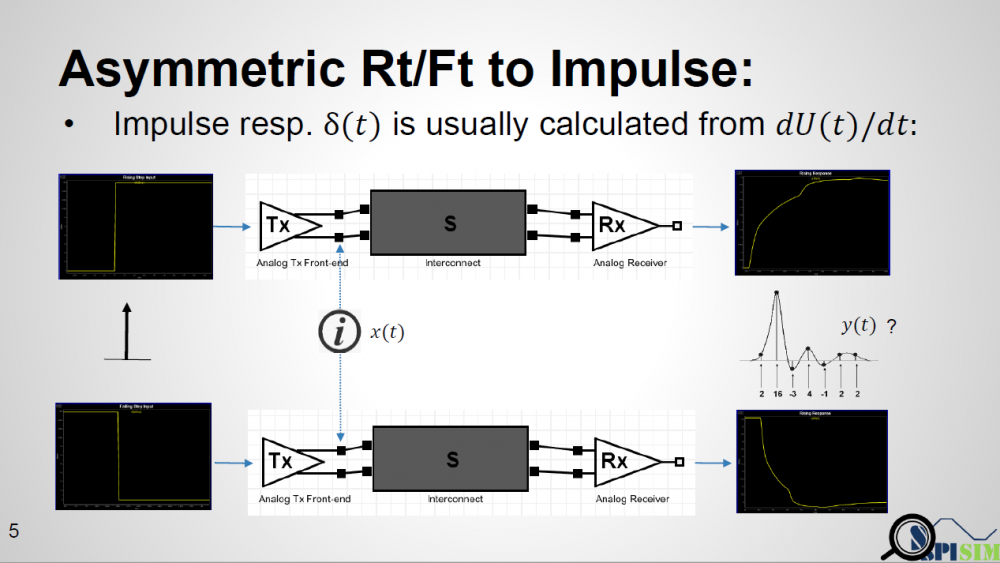
One may think that there is no such limitation that an AMI model can only be called once. So theoretically, a simulator can run analysis flow twice… impulse calculated from rising step response is used for the first time and the one from falling step response is used for the second time. However, not only is this not efficient, a model may not be implemented properly such that calling AMI_Init again right after AMI_Close may cause crash if it’s in the same process and model pointer was not released completely. Thus doing so may hamper a simulator’s robustness.
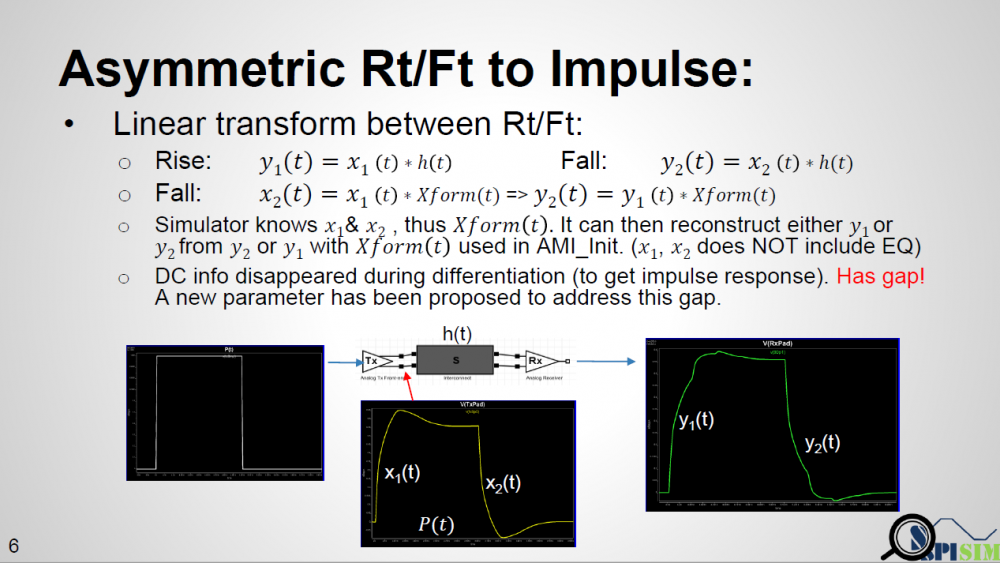
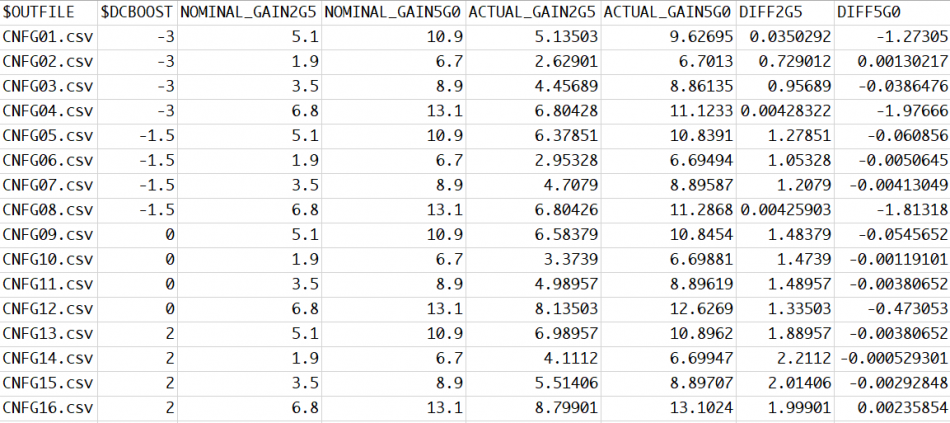
As depicted in the picture above… if a simulator uses a long UI pulse to calibrate the channel, then both rising and falling step response are included in one simulation. Now let the data captured at Tx analog pad as X1 and X2 for rising and falling portion respectively, the data captured at Rx analog pad Y1 and Y2 will be X1 and X2 convolved with interconnect’s transfer function, which is LTI. If we derive a Xform(t) which is transfer function between X1 and X2, then that Xform(t) should also be able to transform between Y1 and Y2. That means if a simulator can calculate Xform(t) it self, then regardless the impulse response it sent to AMI models is calculated from rising or falling step response, it can always “reconstruct” the result from the other type of impulse response using this Xform(t) function.
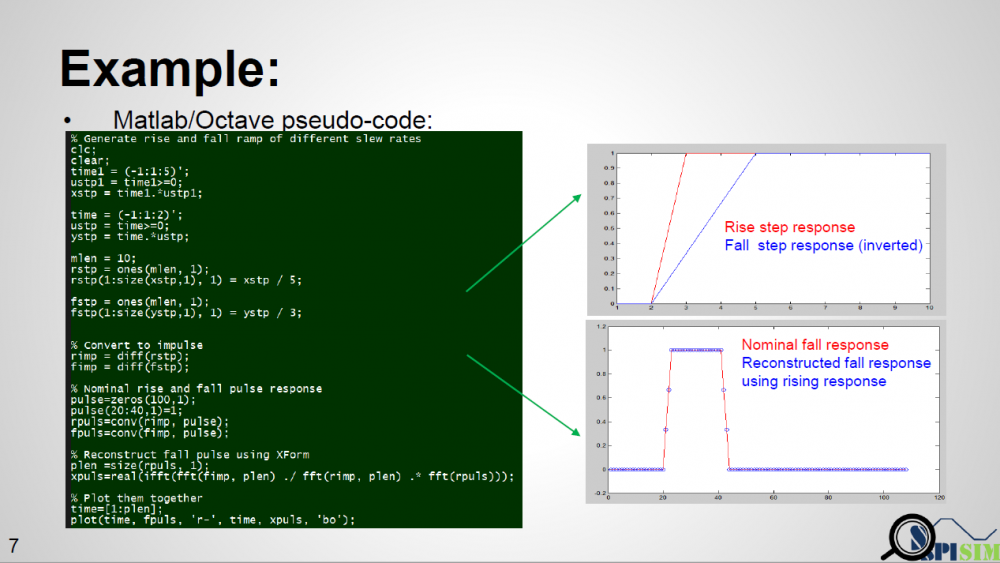
To prove this concept, we have written a simple matlab script taking step inputs of different slew rate, say inp1 and inp2. It calculates the Xform(t) function from both inputs and then reconstruct the response out2′ from out1. When overlaying nominal output out2 and reconstructed out2′ together, we can see that they match very well, thus prove the concept.

Once we have response from both different slew rates, we can construct their respective eyes then use each one’s different portion to construct a synthesized eye. Such eye will not be symmetric like that calculated from SERDES.
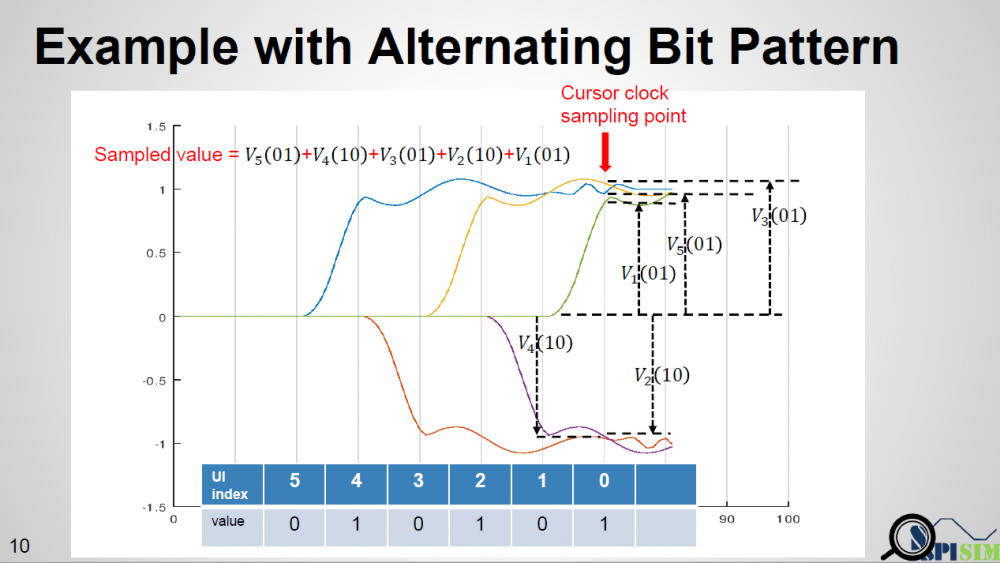
When calculating PDF for asymmetric case, one may also need to consider the precedent bit’s value and use a tree like structure to keep track of possible bit sequence. For example, for a typical SERDES bit sequence, if encoding is not considered, each bit will have 50% one and 50% zero. PDF is constructed based on that assumption. But in an asymmetric case, if the data used at the cursor is from rising response, then the cursor bit must be 1 while (cursor – 1) must be zero. If (cursor – 2) is 1 again, then the tail of falling response at (cursor – 1) will be superimposed to the cursor data. That is, we can’t treat each bit to have same 50% probability when constructing PDF. It’s not a binomial distribution as each occurrence is not independent. A simulator may need to determine the maximum bit length to keep track of first, then based on that depth to form tree-like sequence which leads to the rising or falling steps at the cursor location. Finally use superimpose to construct the overall response.

According to the reference flow for the bit-by-bit case: equalized Tx output from digital bit sequence is converted with channel’s impulse response. The resulting waveform is then sent to Rx EQ before getting final results. Either Tx EQ or Rx EQ or both may not be LTI so usage of aforementioned Xform(t) is not applicable.
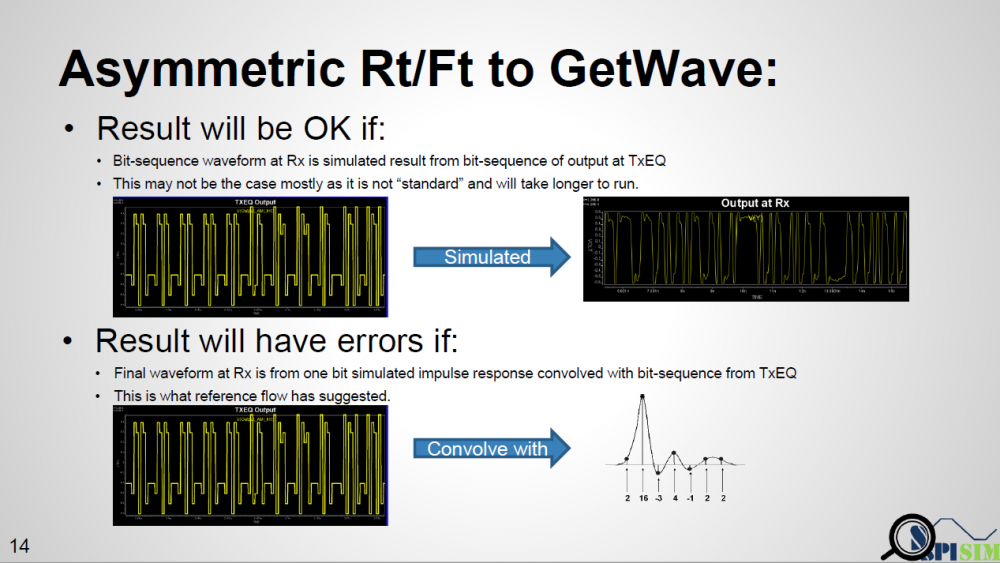
As a fruit of thought… the spec. only mentions that in a bit-by-bit mode, the output of Tx AMI model is equalized digital sequence, while input to the Rx EQ must be the channel response from that sequence, then are there other ways to get such response to Rx yet with different Rt/Ft considered?
One example is like shown in top half of the picture above. If a simulator takes that equalized digital input and “simulate” to get final response, then this “simulation process” should have taken different Rt/Ft into account and has valid results. However, this process will be slow and I don’t think any simulator is doing it this way. Furthermore, the spec. specifically say it needs to “convolve” with impulse response. First of all, this impulse can be from rising or falling. Secondly, even we decide to decovolve with input first (thus has sequences of different delta response) then convolve with pulse response (i.e. one simulated UI), will there be any issue?

From the plot above… we can see that when a pulse has different rising and falling slew rate, using superimpose to construct 011… will find “glitches” at the trailing high state portion. The severity of this “glitches” depends on how much difference the Rt/Ft is. So using a pulse response here will still not work.
A simple matlab script has also been written to demonstrate occurrence of such “glitches”. This proves that not only using an impulse response to convolve with Tx EQ’s output is problematic, even using a full simulated pulse (which has asymmetric Rt/Ft’s effect) to convolve delta sequences (this delta sequence is original TX EQ’s output deconvolve with one digital bit) will still be problematic. Glitches will happen for consecutive ones or zeros due to the mismatches of Rt and Ft. Thus one must use rise step and fall step response instead when doing such kind of convolution.
In this presentation, we discussed how existing AMI flow may be applied to asymmetric Rt/Ft such as those often seen in DDR case. A “smarter” EDA tool should be able to handle this situation without changing on spec.’s reference flow. When a channel analysis is performed in a “statistical” flow, an EDA tool can obtain waveform data at both Tx and Rx analog buffer’s pads during calibration process. Such data can be used to construct a transform function, XForm(t). With this function, impulse response through EQ can be reconstructed and thus built an asymmetric eye. Tree structure may be needed to keep track of possible bit combinations. In a “bit-by-bit” flow, the current spec. may be too specific as it forces to use convolution of TX EQ’s output with channel’s impulse response before sending to RX EQ. Such direct convolution may be problematic. A “smarter” simulator may calculate it using different method without changing data output from TX EQ and input to the RX EQ. Step response should be used as different Rt/Ft will cause “glitches” when consecutive ones/zeros are present if convolution method is used.
Presentation: [HERE] (http://www.spisim.com/support/paperetc/20180202_DesignConSummit_SPISim.pdf)
Audio recording (English): [HERE]
In previous post, I mentioned about the “IBIS cook-book” as a good reference for the analog portion of the buffer modeling. Unfortunately, when it comes to the equalization part, i.e. AMI, there is no similar counterpart AFAIK. For the AMI modeling, the EQ algorithms need to be realized with algorithms/procedures implemented as spec. compliant APIs and written in C language. These functions then need to be compiled as a dynamic library in either dynamic link libraries (.dll on windows) or “shared objects (.so on linux-like). Different compiler and build tool has different ways to create such files. So it’s fair to say that many of these aspects are actually in the computer science/programming domains which are outside the electrical or modeling scopes. It is unlikely to have a document to detail all these processes step-by-step.
In this post, instead of writing those “programming” details, I would like to give a high-level overview about what different steps of the AMI modeling process are… from end to end. Briefly, they can be arranged in the following steps based on execution order:
The following sections will describe each part in details.
Analog modeling:
Believe it or not, the first step of AMI modeling is to create proper IBIS models… i.e. its analog portion. This is particular true if circuit being modeled belongs to TX. A TX AMI model is equalizing signals which includes its own analog buffer’s effect measured at the TX pad. So if there is no channel (pass-through) and it’s under nominal loading condition, the analog response of the TX will be the signals to be equalized. That is to say, without knowing what will be equalized (i.e. what the model’s analog behavior is), one can’t calculate the TX AMI model’s EQ parameters.

Take the plot above as an example. This is a FFE EQ circuit. The flat lines indicated by two yellow arrows are different de-emphasis settings, thus controlled by AMI. However, the rising/falling slew rate, wave shape and dc levels etc as circled in red are all analog behaviors. Thus an accurate IBIS model must be created first to establish the base lines for equalization. Recently, BIRD 194 has been proposed to use touch-stone file in lieu of an IBIS model… still the analog model must be there.
For a RX circuit, it may be easier as an input buffer is usually just a ESD clamp or terminator. Thus it doesn’t take much effort to create the IBIS model. Interested people may see my previous posts regarding various IBIS modeling topics.
Prepare collateral:
AMI’s data can be obtained from different sources: circuit simulation, lab/silicon measurement or data sheet. For simulation case, simulation must be done and the resulting waveform’s performance needs to be extracted. These values will serve as a “design targets” based on whitch AMI model’s parameters are being tuned.
For example, this is a typical TX waveform and measured data:
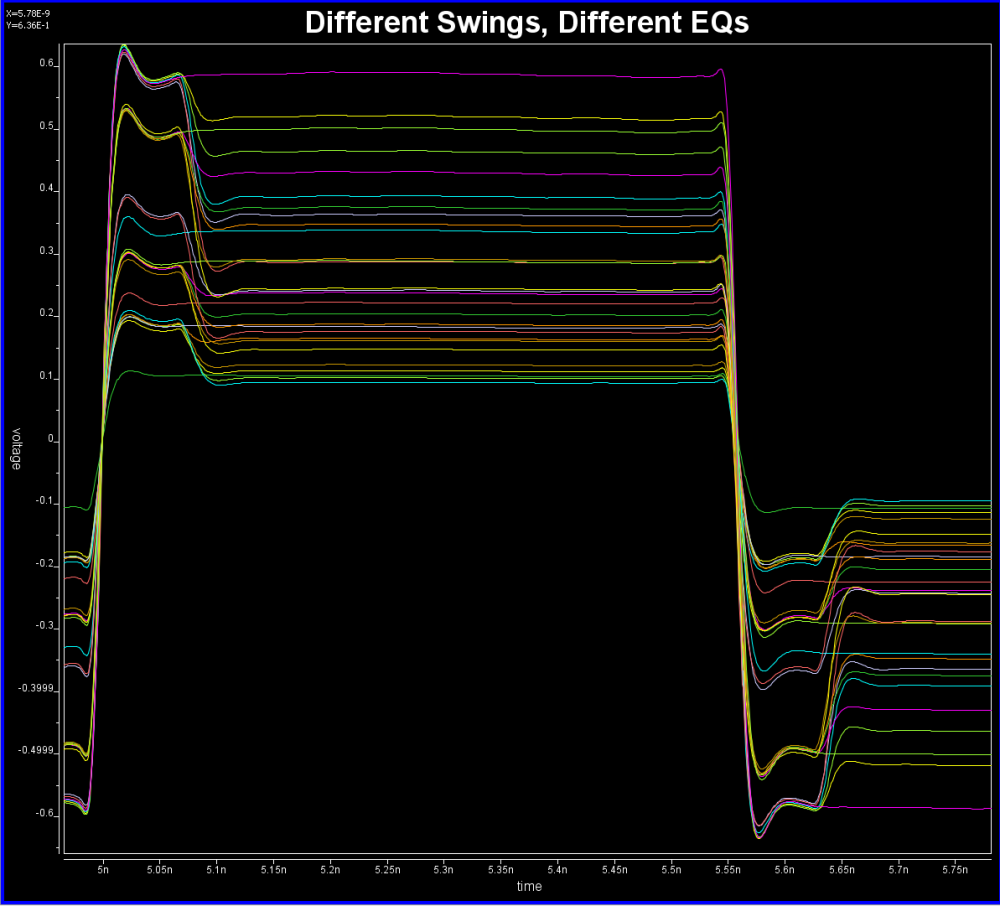
Various curves have been “lined-up” for easy post-processing. Using our VPro, we batch measured the value at the 5.3ns for different curves and created a table: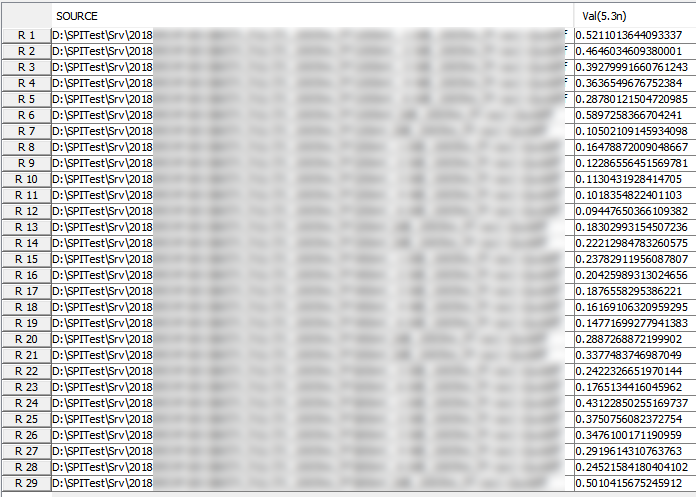 Similarly, data collected from measurement needs to be quantified. This may be done manually and maybe labor intensive as the noise is usually there:
Similarly, data collected from measurement needs to be quantified. This may be done manually and maybe labor intensive as the noise is usually there: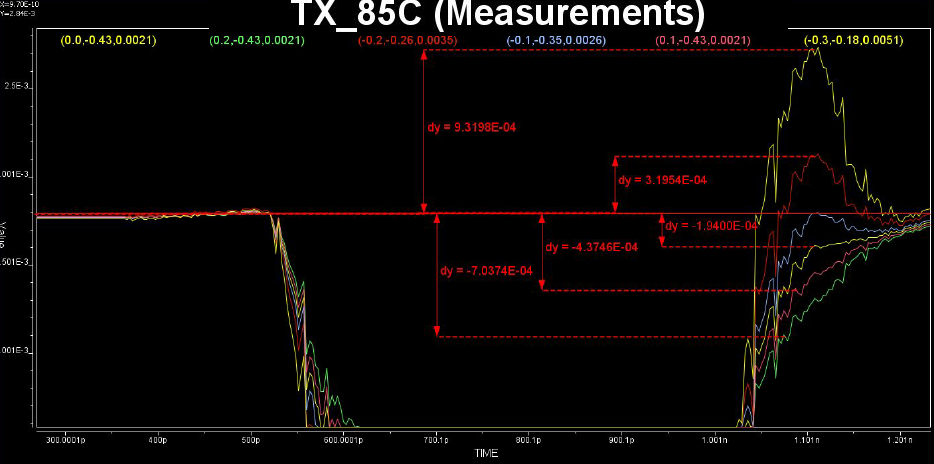
Some of the circuits may have response is in frequency domain. In this case, various points (DC, fundamental freq. 2X fundamental etc) needs to be measured like above.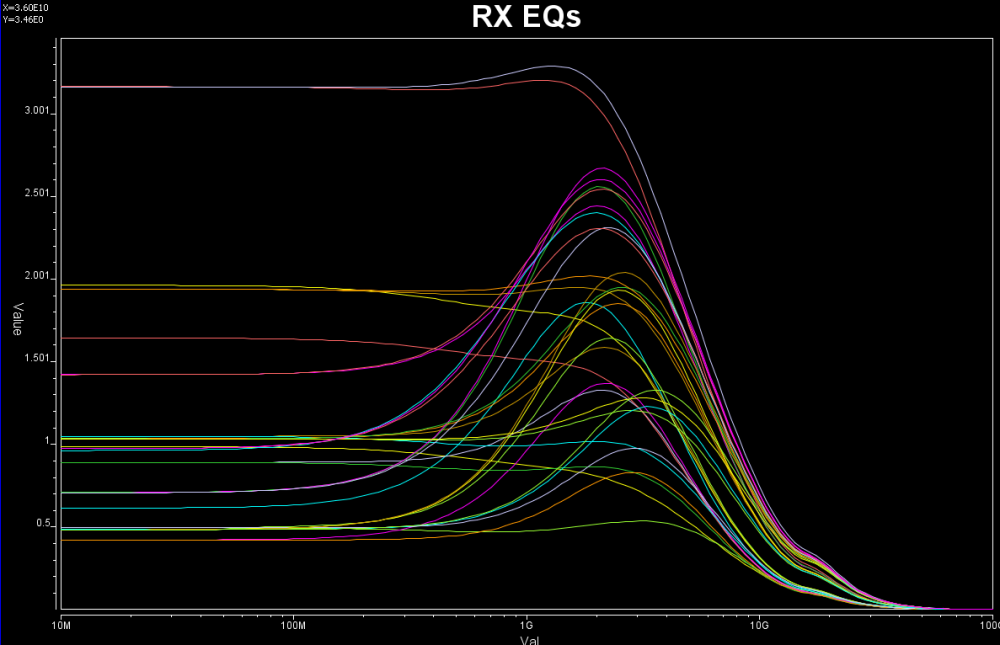
If it’s from data sheet, then the values are already there yet there may be different ways to realize such performance. For example, equations of different zeros and poles locations may all have same DC gain or gain at particular frequencies, so which one to pick may depending on other factors.
Define architecture:
Based on the collateral and the data sheet, the modeler needs to determine how the AMI models will be built. Usually it should reflect the IC’s design functions so there are not much ambiguity here. For example, if the Rx circuit has DFE/CDR functions, then the AMI models must also contain such modules. On the other hand, some data my be represented in different ways and proper judgement needs to be made. Take this waveform as an example: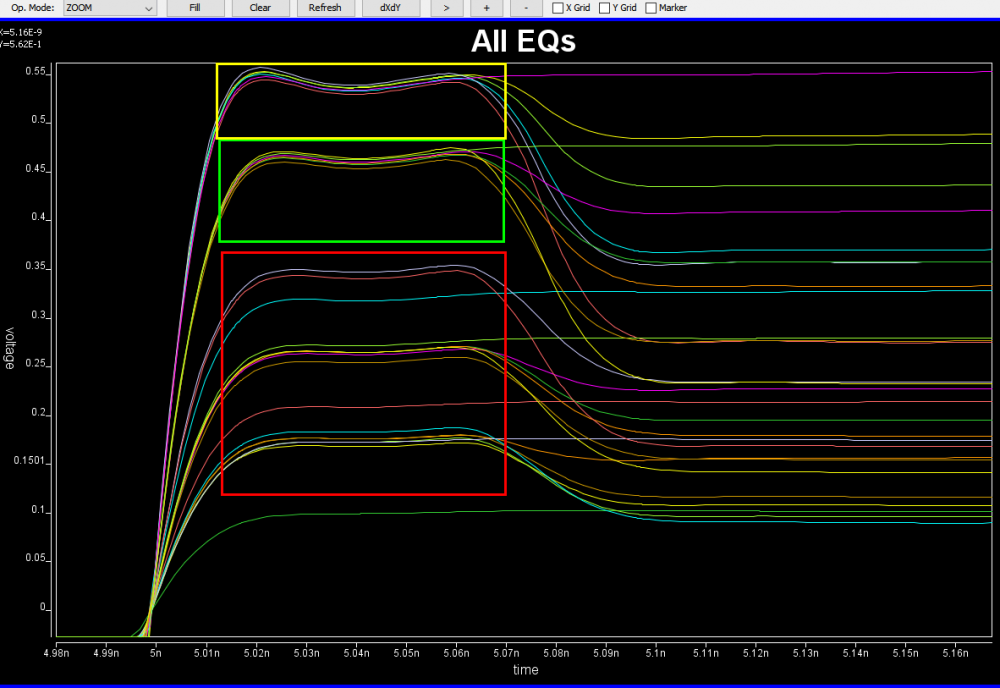
It’s already very obvious that it has a FFE with one post-tap. However, since the analog behavior needs to be represented by an IBIS model, then one needs to decide how these different behaviors, boxed in different colors, should be modeled. They can be constructed with several different IBIS models or a single IBIS model yet with some “scaling” block included so that IBIS of similar wave shapes can be squeezed or stretched. For a repeater, oftentimes people only care about what goes into and what comes out of this AMI model. The abilities to “probe” signals between a repeater’s RX and TX may be limited by the capabilities of simulator used. As a result, a modeler may have freedom determining which functions go into Rx and which go to Tx. In some cases, same model yet with different architecture needs to be created to meet different usage scenarios. An example has been discussed in our previous post [HERE]
Create models:
Once architecture is defined, next step is the actual C/C++ implementation. This is where programming part starts. Ideally, building blocks from previous projects are there already or will be created as a module so that they can be reused in the future. Multiple instance of the same models may be loaded together in some cases so the usage of “static” variables or function need to be very careful. Good programming practice comes into play here. I have seen models only work with certain bit-rate and 32 samples per UI. That indicates the model is “hard-coded”… it does not have codes to up-sample or down-sample the data based on the sampling-interval passed in from the API function. Accompanied with writing model’s C codes are unit testing, source revision control, compilations and dependencies check etc. The last one is particular important on linux as if your model relies on some external libraries and it is not linked statically, the same model running fine on developer’s machine will not even pass golden checker at user’s end…. because the library is not available there. Typically one will need to prepare several machines, virtual or not, which are “fresh” from OS installation and are the oldest “distros” one is willing to support. All these are typical software development process being applied toward this AMI modeling scope.
After the binary .dll/.so files are generated, then next step is to assemble a proper .ami files. Depending on parameter types (integer, values, corners etc), different flavors of syntax are available to create such file. In addition, different EDA simulators has different ways to present the parameter selections to its end user. So one may need to choose best syntax so that choices of parameter values will always be selected properly in targeted simulators. For example, if one already select TYP/MIN/MAX corner for the IBIS model, he/she should not have to do so again for the AMI part. It doesn’t make sense at all if a MIN AMI model will be used with MAX corner IBIS model… the corner should be “synchronized”.
Once the model is ready, next step is to tune the parameters so that each of the performance target will be matched. Some interface, such as PCIe, has pre-defined FFE tap weights so there are no ambiguities. In most cases, one need to find the parameter’s values to match measured or simulated performance. Such tasks is very tedious and error prone if doing manually and process like our “AutoTune” will come very handy:
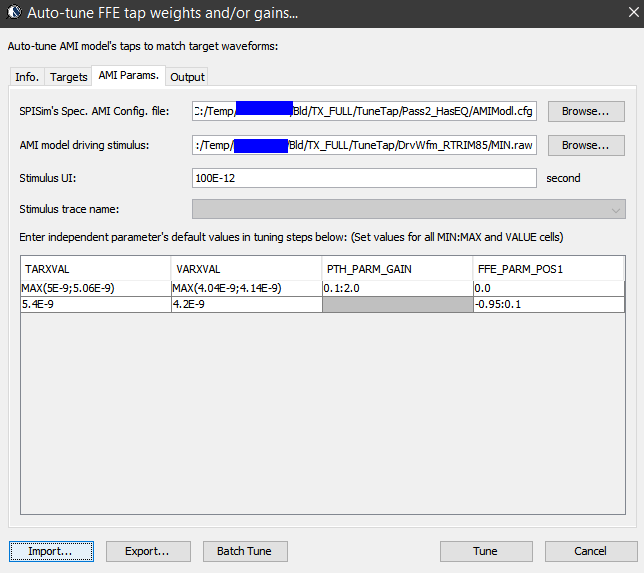
Basically, our tool let user specify matching target and tool will use bisection algorithm to find the tap values. Hundred of cases can be “tuned” in a matter of minutes. In some other cases, grid search may be needed.
Model validation:
Just like traditional IBIS, the first step of model validation is to run it through golden checker. However, one needs to do so on different platforms:

The golden checker didn’t start checking the included AMI binary models until quite recently. Basically it loads the .ibs file, identifies models with AMI functions, then check the .ami file syntax. Finally, the checker will load the associated .dll/.so files. Due to the fact that different OS platform loads binary files differently, that means certain models (e.g. .dll) can only be checked on associated platform (e.g. Windows). That’s why one needs to perform the same check on different platforms to make sure they are all successful. Library dependencies or platform issues can be identified quickly here. However, the golden checker will not drive the binary file. So the functional checks described in next paragraph will be next step.
Typically, an AMI model have several parameters. To validate a model thoroughly, all combinations of these parameters values need to be exercised. We can “parameterize” settings in a .ami file like below:
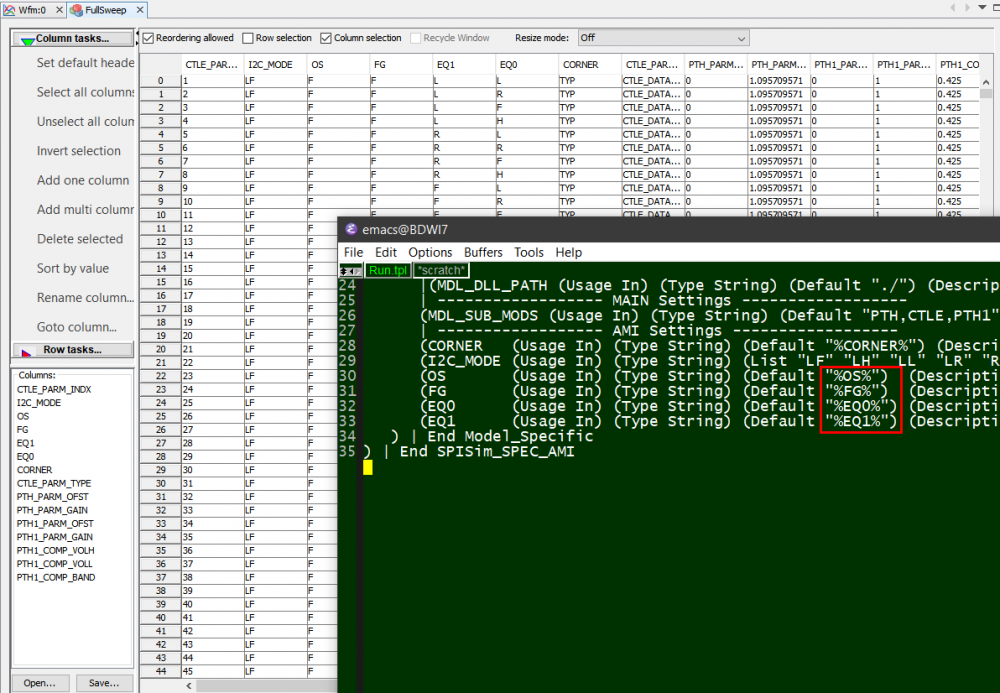
Here, pattern like %VARIABLE_NAME% is used to create a .ami template. Then our SPIMPro can be used to generate all combinations of possible parameter values and create as a table. There can usually be hundreds or even thousands cases. Similar to the process described in “Systematic approach mentioned in my previous post”, we can then generate corresponding .ami files for all these cases. So there will be hundreds or thousands of them! Next step is to be able to “drive” them and obtain single model’s performance. Depending on the EDA tools, most of them either do not have automation capability to do this in batch mode or may require further programming. In our case, our SPIMPro and SPIVPro have built-in functions to support this sweeping flow in batch mode all in the same environment. SPISimAMI model driver is used extensively here! Once each case’s simulation is done, again one needs to extract the performance then compare with those obtained from raw data and make delta comparison.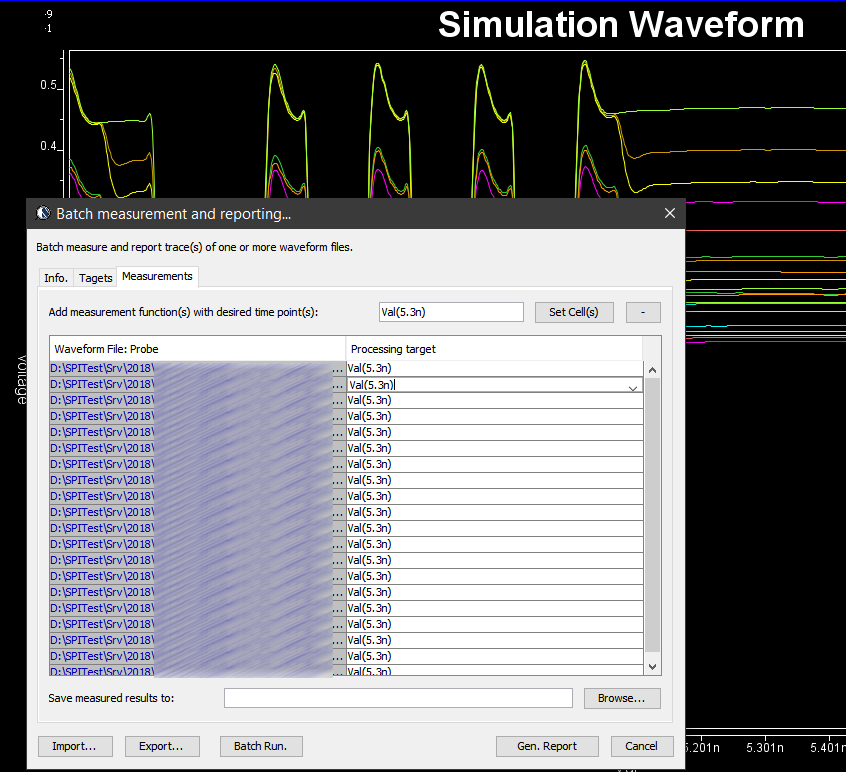
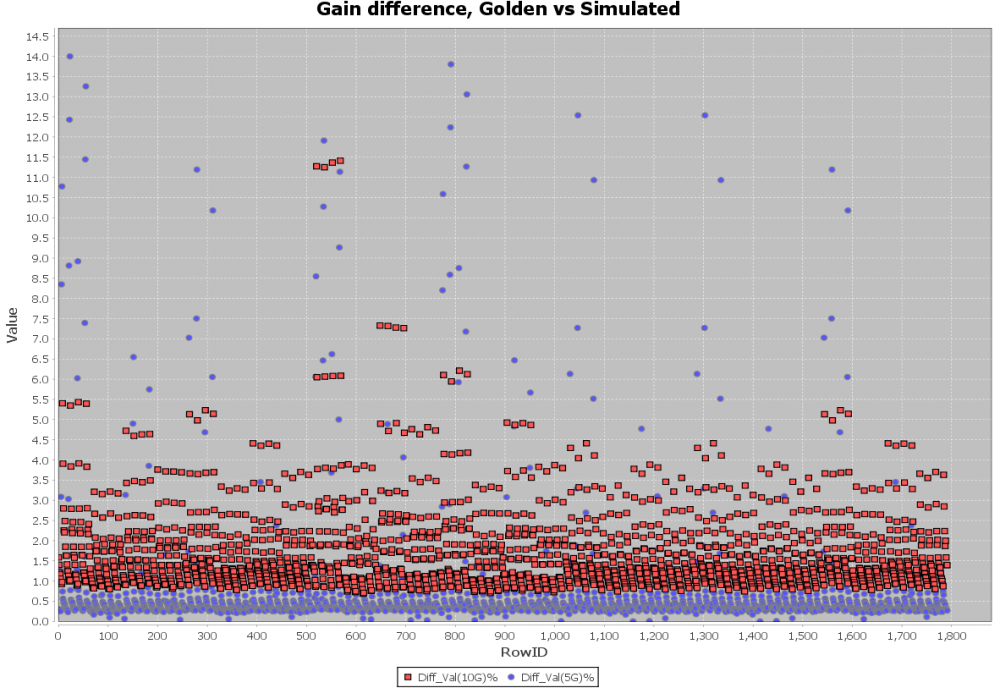
A scattering plot like below will quickly indicate which AMI parameter combinations may not work properly in newly created AMI models. In this case, one needs to go back to the modeling stage to check the codes then do this sweep validation all over again.
Channel correlation:
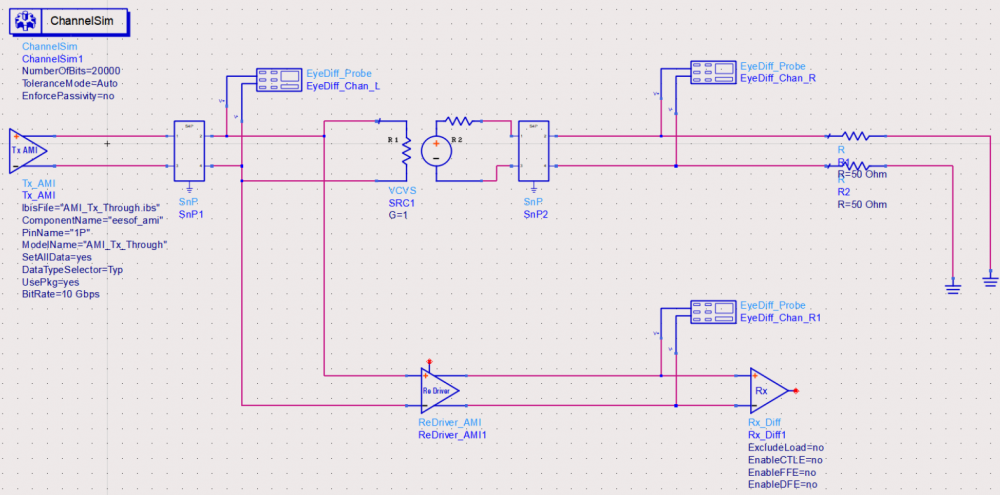
The model validation mentioned in previous section is only for a single model, not the full channel. So one still needs to pick several full channels set-up to fully qualify the models. A caveat of the channel analysis is that it only shows time domain data regardless the flow is “statistical” or “bit-by-bit”, that means it is often not easy to qualify frequency domain component such as CTLE. In this case, a corresponding s-parameter whose Sdd12 (differential input to differential output) is represented by this CTLE AMI settings can be used for an apple-to-apple comparison, like schematic shown below:
Another required step here is to test with different EDA vendor’s tool. This presents another challenge because channel simulator is usually pricey and it’s rarely the case that one company will have all of them (e.g. ADS, HyperLynx, SystemSI, QCD and HSpice etc). Different EDA tools does invoke AMI models differently… for example, some simulator passes absolute path for DLL_Path reserved parameter while others only sent relative path. So without going through this step, it’s difficult to predict what a model will behave on different tools.
Documentation:
Once all these are done, the final step is of course to create an AMI model usage guide together with some sample set-ups. Usually it will starts with IBIS model’s pin model associations and some performance chart, followed by descriptions of different AMI parameters’ meaning and mapping to the data sheet. One may also add extra info. such as alternatives if the user’s EDA tool does not support newer keyword such as Dll_Path, Dll_ID or Supporting_Files etc. Waveform comparison between original data (silicon measurement vs AMI results) should also be included. Finally it will be beneficial to provide instructions on how an example channel using this model can be set-up in popular EDA tools such as ADS, HyperLynx or HSpice.

Summary:
There you have it.. the end-to-end AMI modeling process without touching programming details! Both AMI API and programming languages are moving targets as they both evolve with time. Thus one must continue honing skills and techniques involved to be able to deliver good quality models efficiently and quickly. This is a task which requires disciplines and experience of different domains. After sharing these with you readers, do you still want to do it yourself? 🙂 Happy modeling!
Continuous time linear equalizer, or CTLE for short, is a commonly used in modern communication channel. In a system where lossy channels are present, a CTLE can often recover signal quality for receiver or down stream continuous signaling. There have been many articles online discussing how a CTLE works theoretically. More thorough technical details are certainly also available in college/graduate level communication/IC design text book. In this blog post, I would like to focus more on its IBIS-AMI modeling aspect from a practical point of view. While not all secret sauce will be revealed here:-), hopefully the points mentioned here will give reader a good staring point in implementing or determining their CTLE/AMI modeling methodologies.
[Credit:] Some of the pictures used in this post are from Professor Sam Palermo’s course webpage linked below. He was also my colleague at Intel previously. (not knowing each other though..)
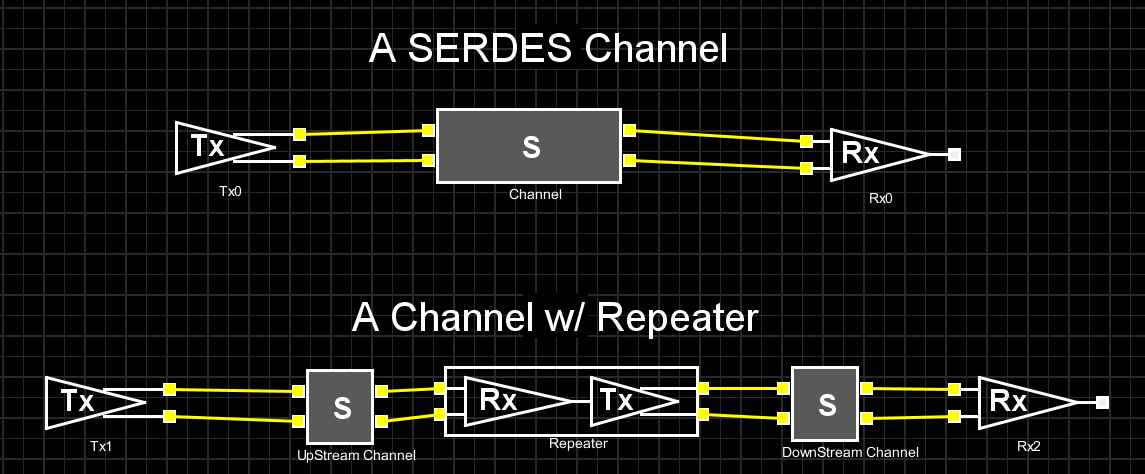
The picture above shows two common SERDES channel setups. While the one at the top has a direct connection between Tx and Rx, the bottom one has a “repeater” to cascade up stream and down stream channels together. This “cascading” can be repeated more than once so there maybe more than two channels involved. CTLE may sit inside the Rx of both set-ups or the middle “ReDriver” in the bottom one. In either case, the S-parameter block represents a generalized channel. It may contain passive elements such as package, transmission lines, vias or connectors etc. A characteristic of such channel is that it presents different losses across spectrum, i.e. dispersion.
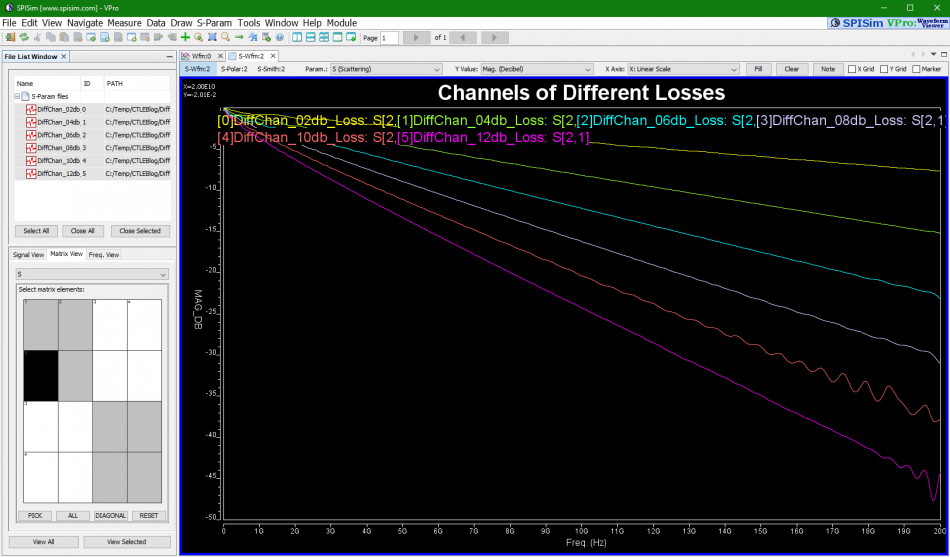
For example, if we plot these channel’s differential input to differential output, we may see their frequency domain (FD) loss as shown above.
Digital signals being transmitted are more or less like sequence of bit/square pulse. We know that very rich frequency components are generated during its sharp rising/falling transition edges. Ideally, a communication channel to propagate these signals should behave like an (unit-gain) all pass filter. That is, various frequency components of the signal should not be treated equally, otherwise distortion will occur. Such ideal response can be indicated as the green box below:

In reality, such all pass filter does come often. In order to compensate our lossy channels (as indicated by the red box) to be more like the ideal case (green box) as an end result, we need to apply equalization (indicated by blue box). This is why an equalizer is often used… basically it provides a transfer function/frequency response to compensate the lossy channel in order to recover the signal quality. A point worth taken here is that the blue box and red box are “tie” together. So using same equalizer for channels of different losses may cause under or over compensated. That is, an equalizer is related to the channel being compensated. Another point is that CTLE is just a subset of such linear equalizer.
A linear equalizer can be implemented in many different ways. For example, a feed-forward equalizer is often used in the Tx side and within DFE:
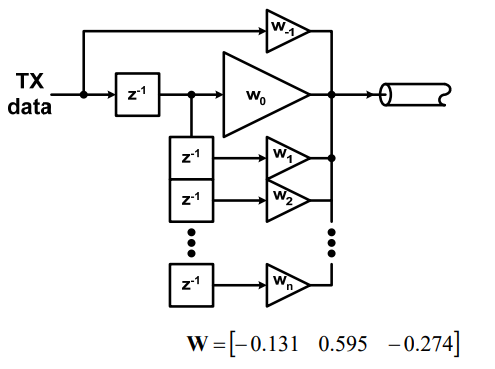
FFE’s behavior is more or less easier to predict and its AMI implementation is also quite straight forward. For example, a single pre-tap or post-tap’s FFE response can be easily visualized and predicted:
Now, a CTLE is a more “generalized” linear equalizer, so its behavior is usually represented in terms of frequency responses. Thus, to accommodate/compensate channels of different losses, we will have different FD responses for CTLE:
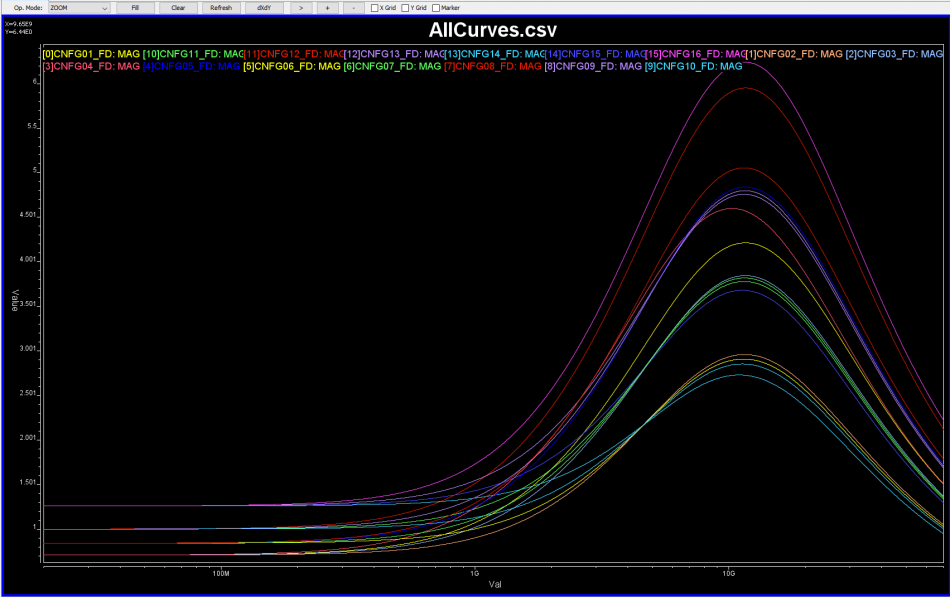
Now that IBIS-AMI modeling for CTLE is of concern, how do we obtain such modeling data for CTLE and how they should be modeled?
While CTLE’s behavior can be easily understood in frequency domain, for IBIS-AMI or channel analysis, it eventually needs to come back to time domain (FD) to convolve with inputs. This is because both statistical or bit-by-bit mode of link analysis are in time domain. Thus we have several choice: provide model FD data and have it converted to TD inside the implemented AMI model, or simply provide TD response directly to the model. The benefit of the first approach is that model can perform iFFT based on analysis’ bit rate and sampling rate’s settings. The advantage of the latter one is that the provided TD model can be checked to have good quality and model does not need to do similar iFFT every time simulation starts. Of course, the best implementation, i.e. like us SPISim’s approach, is to support both modes for best flexibility and expandability 🙂
Depending on the availability of original EQ design, there are several possibilities for FD data: Synthesized with poles and zeros, extract from S-parameters or AC simulation to extract response.
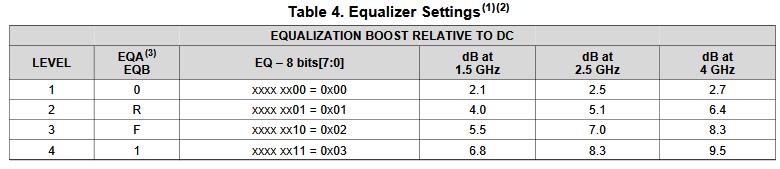
 So say if we are given a data sheet which has EQ level of some key frequencies like below:
So say if we are given a data sheet which has EQ level of some key frequencies like below: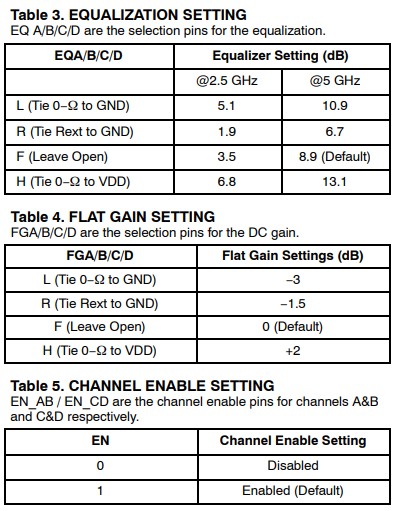 Then one can sweep different number and locations of poles and zeros to obtain matching curves to meet the spec.:
Then one can sweep different number and locations of poles and zeros to obtain matching curves to meet the spec.: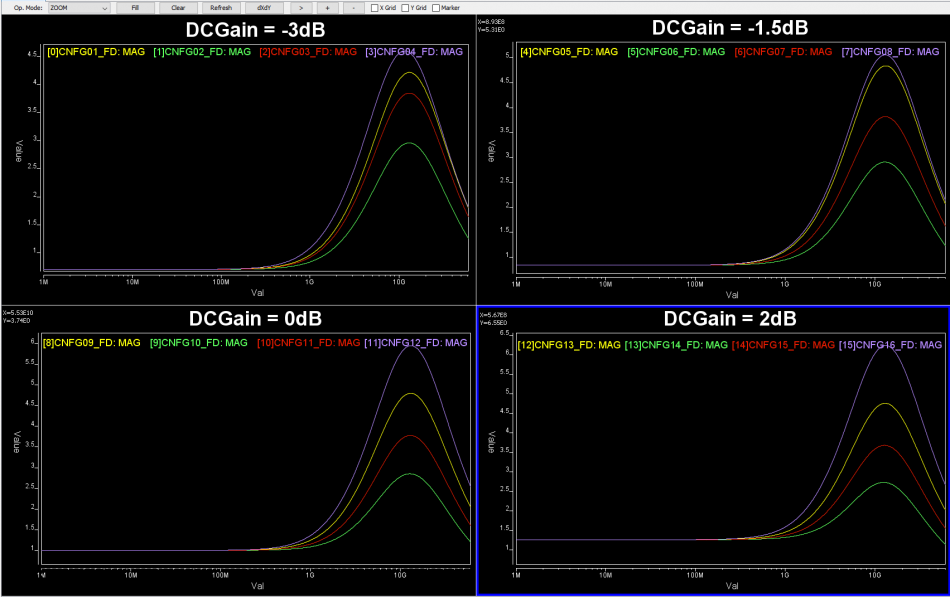 Such synthesized curves are well behaved in terms of passivity and causality etc, and can be extended to covered desired frequency bandwidth.
Such synthesized curves are well behaved in terms of passivity and causality etc, and can be extended to covered desired frequency bandwidth.

Now that we have data to model, how will they be implemented in C/C++ codes to support AMI API for link analysis is another level of consideration.
Typically, such adaptive mechanism has a pre-sorted CTLE in terms of strength or EQ level, then a figure-of-merit (FOM) needs to be extracted from equalized signal. That is, apply a tentative CTLE to the received data, then calculate such FOM. Then increase or decrease the EQ level by using adjacent CTLE curves and see whether FOM improves. Continue doing so until either selected CTLE “ID” settles or reach the range bounds. This process may be performed across many different cycles until it “stabilized” or being “locked”. Thus, the model may need to go through training period first to determine best CTLE being used during subsequent link analysis.
So now you have a bunch of settings or data like below, how should you architecture the model properly such that it can be extended in the future with revised CTLE response or allow user to perform corner selections (which essentially adds another dimension):
This is now more in software architecture domain and needs some trade-off considerations. For example, you may want to provide fine grid full spectrum FD/TD response but the data will may become to big. So internal re-sampling may be needed. For FD data, the model may needs to sample to have 2^N points for efficient iFFT. Different corner/parameter selection should not be hard coded in the models because future revised model’s parameter may be different. For external source data, encryption is usually needed to protect the modeling IP. With proper planning, one may reuse same CLTE module in many different design without customization on a case-by-case basis.
Finally it’s time to correlate the create CTLE AMI model against original EQ design or its behavioral model. Done properly, you should see signals being “recovered” from left to right below:
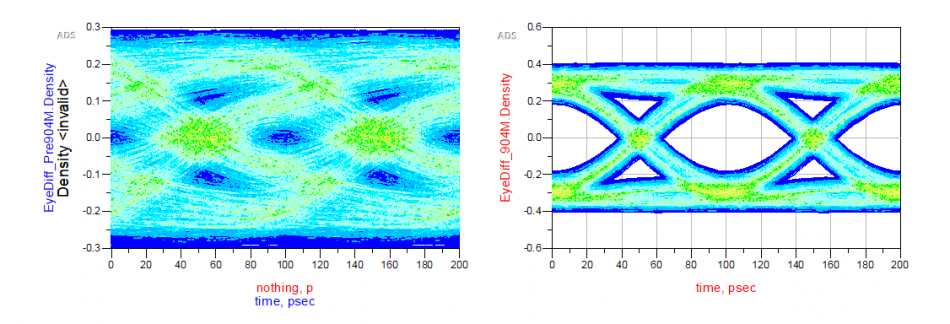
However, getting results like this in the first try may be a wishful thinking. In particular, the IBIS-AMI model does not work alone… it needs to work together with associated IBIS model (analog front-end) in most link simulator. So that IBIS model’s parasitics and loading etc will all affect the result. Besides, the high-impedance assumption of the AMI model also means proper termination matching is needed before one can drop them in for direct replacement of existing EQ circuit or behavioral models for correlation.
At this point, you may realize that while a CTLE can be easily understood from its theoretic behavior perspective, its implementation to meet IBIS-AMI demands is a different story. We have seen CTLE models made by other vendor not expandable at all such that the client need to scratch the existing ones for minor revised CTLE behavior/settings (also because this particular model maker charges too much, of course). It’s our hope that the learning experience mentioned in this post will provide some guidance or considerations regardless when you decide to deep dive developing your own CTLE IBIS-AMI model, or maybe just delegate such tasks to professional model makers like us 🙂
In previous several posts, we talked about IBIS modeling of analog buffer front end. In today’s post, we are going to give an overview of the modeling of the algorithmic portion which provide equalization to both TX and RX. These algorithmic blocks are usually modeled with IBIS AMI, the “Algorithmic Modeling Interface” portion of the IBIS spec.
IBIS AMI’s scope:
The figure above represents the channel from end to end. The passive channel is composed of various passive elements, such as PCB traces modeled with transmission lines and vias, connectors modeled with s-parameters. The pink block is the analog buffer which acts as front end to interface to the channel directly. They are usually modeled in IBIS. In the TX portion before the front end, and RX portion after that, are equalization circuits. They can be modeled in IBIS AMI. So the AMI model actually works with IBIS to complete the both TX and RX path from latch to latch, instead of pad to pad. In an IBIS model which use AMI, one will find a statement like below, which points to the AMI’s parameter file in .ami extension, and the compiled portion in either .dll (dynamic link library on windows), or .so (shared object on linux), and the IDE with which these .dll/.so files are produced.
Why IBIS AMI:
The main quantitative measure of signal integrity are eye height and eye width of an eye plot. From eye plot, bit-error rate (BER) or other plot like bath tub curve can be derived. The eye plot is formed by folding many bits in time domain with waveform representing the response of these bit sequences. When doing end-to-end channel analysis with transistor buffer or traditional IBIS model, one have to go through actual simulation to obtain such waveform. This is very time consuming and can only acquire very limited number of bits. In order to speed up the process, waveform synthesis is desired, thus brings the need of a new spec. and the invention of AMI. With this performance requirement for technical considerations included, the following lists why IBIS AMI is required:
What is in IBIS AMI:
Now that we know the scope and application of the AMI, let’s take a look at its components in more details. Depending on your perspective:
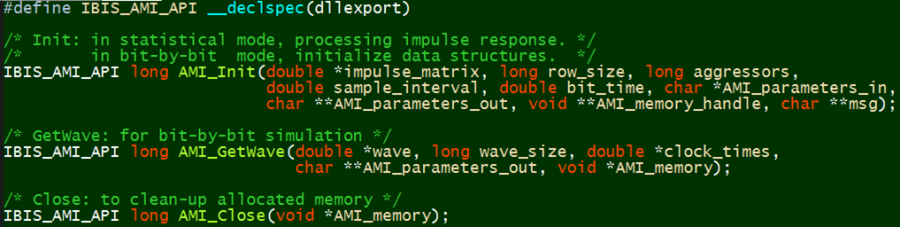
.dll/.so:
IBIS AMI usage scenarios:
An AMI model developer can’t foresee how the developed models will be used. However, the model’s implementation itself will impose such limitation. There are two modes of AMI operations: Statistical or Empirical. If the “GetWave” function is not implemented, the model will only be able to run in “Statistical Flow”, meaning the passive channel must be LTI. On the other hand, if “GetWave” function is implemented, then the model may also run in “Empirical Flow”, which allows non-LTI channel. The figure below gives an overview of the two modes of AMI operations:
In reality, TX and RX AMI models may be from different vendors. Thus their combination also set the limits on how the models can be used. Interested user may see the section 10 of the IBIS spec. for detailed operation explanations.
This post gives a brief overview of IBIS AMI. The modeling flow of AMI model impose a challenge to the model developers. They usually need to know more inside details about the EQ design rather than doing black-box modeling approach. Besides, the extracted EQ algorithms along with their parameters must be coded in C/C++ at least in order to compile and generate required .dll/.so files. Lastly, the flow is more or less EQ implementation dependent (depends on which high-level language the EQ was designed) and the model validation also requires deeper knowledge about the signal integrity. It’s common to have both EDA and SI expertise like what we have here at SPISim to work closely with IC vendors to deliver such models in good qualities. In the future posts, we may come back to cover all these steps and topics in more details.