In previous post regarding simulator development, we mentioned that simulator at its core is linear algebra (with or without relaxation) solving matrices formed to describe netlist’s nodal cutset (KCL) and mesh loops (KVL). We also mentioned that the “hot-loop” of circuit simulation are the “solve” and “stamp” routines, i.e., device solve modeling equations at that particular dc point or time-step then put contents into the aforementioned matrix formation. So a lot of thinking needs to go into formulating these two steps such that simulator developed is stable, maintainable and extensible.
On the p170 of the classic “Computer Methods for Circuit Analysis and Design” book, stamping for basic elements are listed:
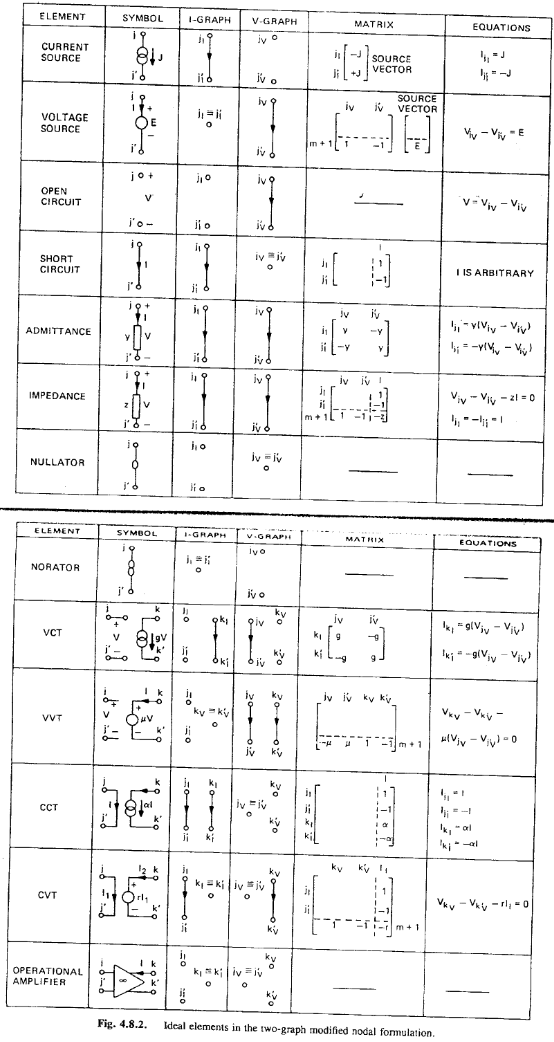
So the first level of abstraction, also the main work of “Solve” routine within each device, is to solve the modeling equations using terminal conditions (i.e. voltage or current) in a particular iteration, then translate into corresponding I, V, Y (admittance), G (conductance) then put into the circuit matrix for simulator to solve. In addition, because Newton method requires first derivative to progress and find next possible root, the “partial” value (first derivative of matrix) also needs to be computed by the device model and provide to the simulator accordingly. Without this, simulator will need to perform numerical derivative (auto-partial) to call “solve” and “stamp” routine multiple times in order to find the derivative dV/dI, or dI/dV etc at that particular terminal conditions. This will result slowness and instability of the circuit simulation.
Each device, regardless how non-linear it is, may be “linearized” to simple equivalent circuit under certain condition. This “certain condition” can be fixed time point, or fixed terminal condition like voltage supply. That is, within each Newton iteration (thus only belong to that iteration and that time point), one may transform non-linear device model into a simple linear equivalent one. Mostly using Norton or Thevenin theorems:
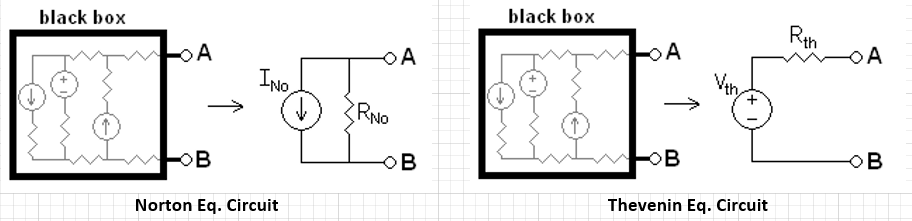
As to how to represent a device model into such linear circuit depends on the device’s physics. In my mind, this is where (device) physics comes into play in the simulator development.
For example, for simple elements like R, V, I, one can simply “stamp” entries by the book. Control sources can also be considered as (controlled) conductance, admittance and “stamp” accordingly. Complicated devices such as transistor, transmission line or S-parameters certainly need some mathematical derivation in advance. Katzenelson algorithm may be used in some condition to solve PWL network. Even devices like L and C also needs special consideration, such as numerical integration and prediction.

The derivative forms for C and L above show that there is no direct solution to find L and C’s conductance or admittance in time domain. So numerical differentiation approach like Backward Euler may be used to calculate conductance value based on circuit history, i,e, result of previous time steps. If this is a fixed-time step simulator, then task will be easier. A variable time step simulator will certainly need much more consideration: how big a time step can be taken, what is the integration or resulted differentiation error etc. Even within device level, such as transmission line and s-parameter, the device it self also must keep track of past history so that reflection from the other end will happen at the right time. From the discussion up to this point, it should be convincing that the simulator development requires multiple disciplines.
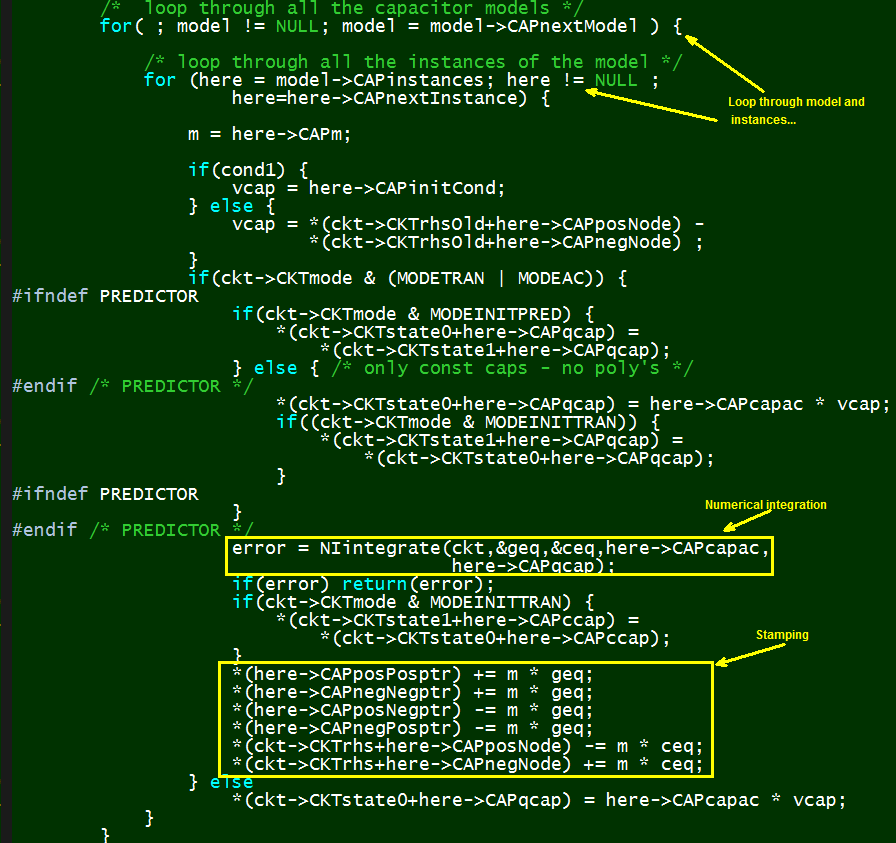
The second level of abstraction happened at the architecture level. There are only 26 English characters but there are much more for device types… some may be even custom made like antenna or macro circuits. So while elementary devices like R, L, C, I, V, E, F, G, H etc all have their own prefixes in the netlist, a mechanism must be in place such that the simulator can support more (some future) devices. This is mostly done using dynamic link library with predefined interfaces and access. The example below is API from Berkeley spice:
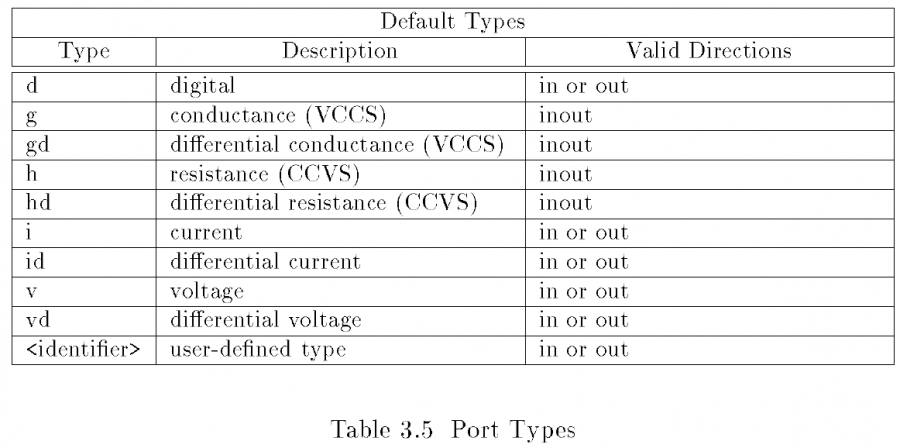
By defining these port types and access functions, the simulator limits the device’s accessibility to its internal structure and even matrices, thus can be more stable. At the same time, the defined interface also allows extensible for future devices. It is thus the device designers he or she needs to map the device under modeling to the limited, predefined interfaces such that the data can be used by simulator at the top and simulate accordingly.
After all these are sorted out, then the remaining part of the simulator development is to figure out physics of the devices, construct a model, realize that model using numerical techniques, solve and extract equivalent’s values at that particular time and iteration, and pass the data back to main caller functions then wait to see whether this solution converges for this iteration. If so, then perform book keeping either for future time step reference, or predict maximum time step simulator can take based on device’s limitation (e.g. break point in PWL sources or transmission line delay).
In SPISim’s SSolver, we reference the Berkeley architecture profoundly and focus more on the device modeling and integration. Existing spice does not have support of any devices required for system analysis, such as IBIS, Lossy coupled, transmission line, S-parameters. Even S-parameter extraction is also very tedious and limited to only two ports originally. While our experience in the past enables us to grasp the simulator architecture easily and build up functionalities much quickly, it is still respectful for us when reading the relative document and source codes when the Berkeley team developed such simulator in the first place several decades ago.

