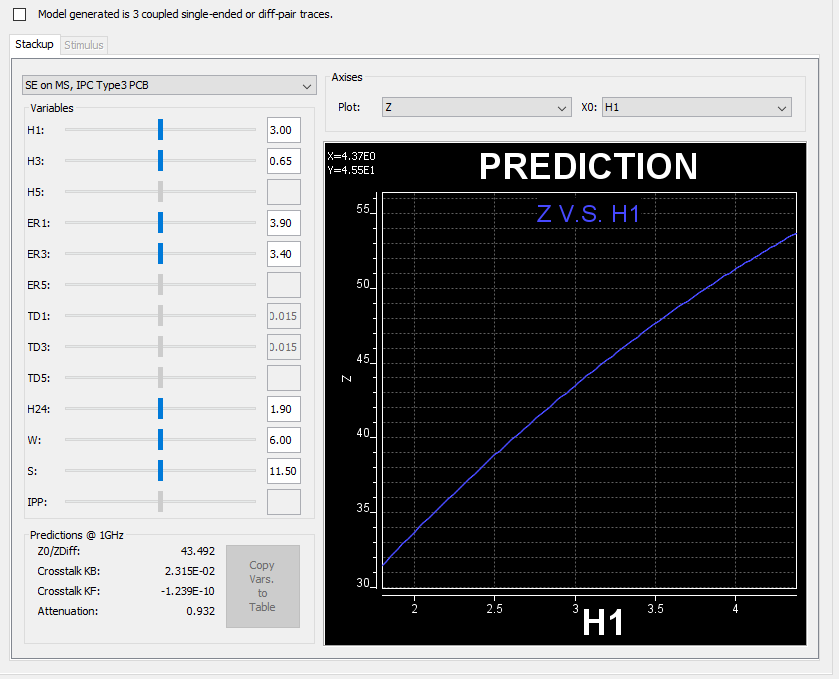
在前一則貼文中, 我們提到若欲找到”一個“方案時, 線性的假設性分析是一個不錯的優化方式。然而當我們要把更多的設計變數放在一起通盤考量來對更大的解答空間裡求最佳化時, 則必需要有更系統性的、而非挑一兩個變數在固定其它變量於一常數值、的優化程序。
反應曲面模型( Response surface model, RSM):
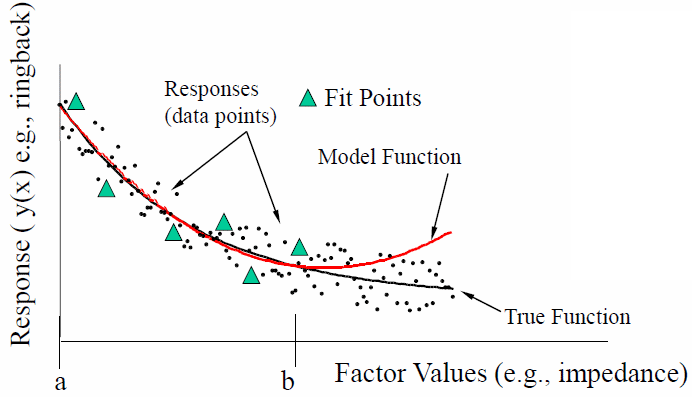
在下圖中, 系統輸出Y1, Y2等同時含有可控制變量X及不受控變量Z; 在其它如晶片設計或晶圓廠裡,諸如不可預測的宇宙射線等對載體的影響便可歸類於這些不受控變數;但在透過仿真來得到輸出結果的整合性分析裡, 過程與結果都是確定性(deterministic)的; 也就是說只要輸入情況一樣, 輸出結果每次也都會相同, 所以這些不受控變數Z便可忽略不計; 我們可以把這種輸入轉成輸出的關係看做是一個具有多維空間的反應曲面, 在這曲面上找頂點或最低點便是最佳化的過程。
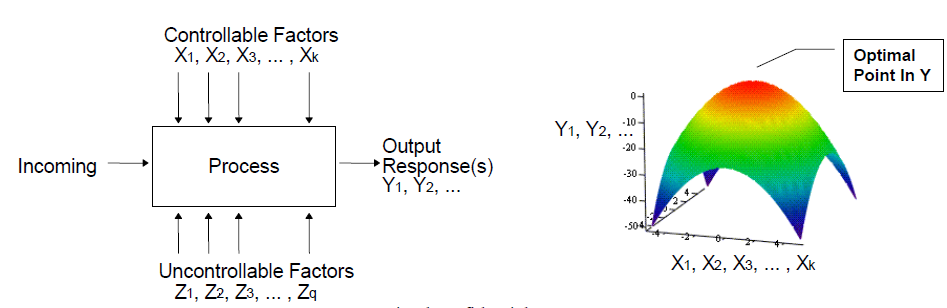
這種輸出入間的對應一般稱為”反應曲面模型” (response surface model, or RSM), 透過在解答間裡的諸多取樣點並對其(透過仿真或場解)求輸出後構間出這樣的一個多維模型來優化便是一種系統性的優化流程; 而實驗設計法(design of experiments, or DOE)則是最常與RSM一起運作的建模程序。
實驗設計法 (Design of experiments, DOE):
當系統有許多變量且各含有一定範圍及可能值時, 要透過全面完整組合(full combinatorial, or full grid)來找最佳值是不大可能的; 我們只能透過極有限取樣點來得到反應以建構出RSM。
將上圖中輸出Y寫成是一個由變量x1, x2 ~ xn所形成的函數f(x), 則透過Taylor Theorem, 這些函式f(x)均可以級數的形式來近似:
當更高階級數(bigger alpha)被包含Taylor級數時, 這近似式與原f(x)就更接近了, 這就好比對時域方波做傅利葉轉換時, 若頻域上包含的諧波更高, 則再反轉回時域時就更近似原來的方波。
在現實世界裡, 大部份的現象主要來自於低階的項目的影響, 若我們只取到二階, 則上述的Taylor級數展開後可寫成如下的二次式:
![]()
當變數X1, X2的值不同時, 等式左邊的輸Yfit值也就不同, 而系數Beta則決定了各變量對輸出的影響程度: beta值愈小, 則變量就更為次要; 那要怎麼算出相關係數Beta呢? 如果我們有N個取樣點, 則上面這種型式的等式寫在一起時便可以如下的矩陣的樣式來表現:
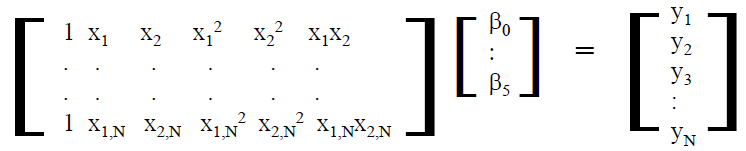
當將二階拉高為至K階時, 則廣義的矩陣式便可寫成如下:
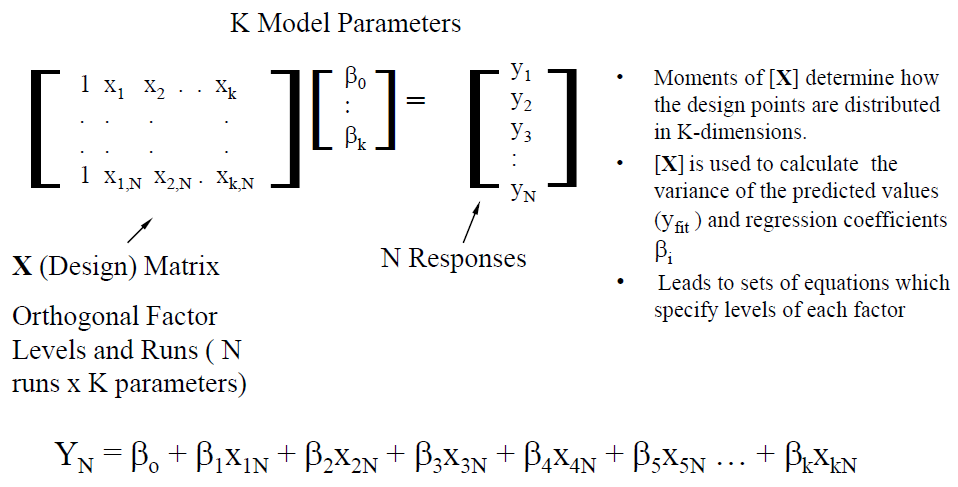
最左邊的X矩陣大多不是方陣, 所以若要求出相關系數Beta的向量, 則需使用一般線性代數裡的操作技巧:擬反矩陣(pseudo inverse)及奇異值分解(singular value decomposition, or SVD), 而所得的係數是在以最小的平均誤差(mean square error)的情況下的解。
欲使用DOE/RSM流程來進行優化, 則有幾項前置作業必需完成:
- 決定有那些變量X及最高階為何: 如能先有洞見, 則取較具相關性的變量可使建構出的模型更近似;其次, X的數目及階數也影響了欲進行仿真的數目及最後矩陣的大小;
- 決定取用那些輸出函數Y: 因為我們只用低階的X來置入Taylor級數, 故若是結果得再經過複雜的數學運算或後處理,則過程間的高階操作便可能打破了低階X和Y的關連性;
- 決定那種取樣方式:在上面矩陣式中, 每一列都是一個系統仿真, 我們只要能在解答空間裡有足夠數目及涵蓋性的取樣點便可, 過多或過少都會影響建出模型的品質; 而這取樣點的方式在統計學上則有許有許多不同的理論可採用。
以實驗設計法優化的流程:
欲利用實驗設計法在對信號或電源完整性上優化; 一般來說有下列步驟:
- 定義變數: 儘量只將主要變量列如分析的範圍則模型才有意義且建模才有效率; 而主要變量則可透過:線性掃描(linear sweep), 假設性分析, 之前產品設計的分析及經驗等等來決定; 再者實驗設計法通常不會只進行一次, 在每次結果出來後對相關係數的檢視都可為下次再進行分析做參考。
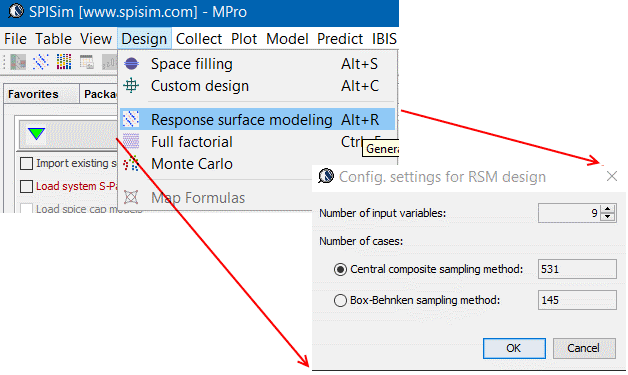
- 定義取樣點: 取樣方式及數目取決於變量多少及範圍; 在信號/電源完整性的應用上, 一般若變量數目在10左右, 則central composite design 是一個不錯的選擇, 如此選出的取樣點在一千到數千個之間; 若是有更多的變量(<=30), 則使用D-Optimal較佳, 取樣法亦和建模方式有關, 當欲建模型不是透過RSM, 而是由神經網路的方式時, 則二次式的需求便未必需要, 故而可用如space filling等取樣法來進行;所述這些都是統計學上的應用, 故許多統計軟體都可拿來設計相關實驗;在我們的建模模組MPro裡, 則有許多常用的有關的內建:
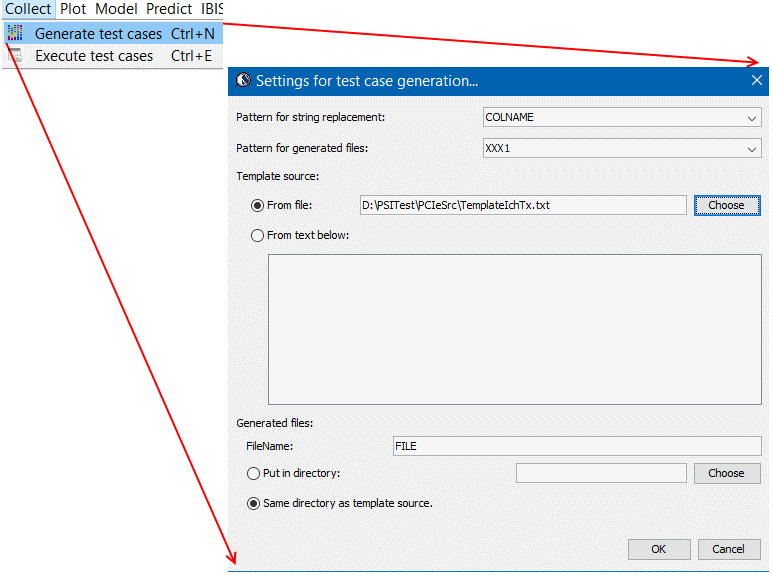
- 產生測試案例: 所定變量一般可分為連續性變量(如電阻值)及非連續性(如各corner等),雖然在變量可能值範圍內有不同的階度可選, 但在上一步驟的取樣點裡, 每一個變數一般只用-1, 0, +1來表示其最小,中間及最大值以用於其案例; 故接下來竹的步驟就是把這取樣點的設定轉為實際的案例以便進行仿真或場解。若是佈線前的分析, 則案例多是Spice的網表(netlist), 故案例的產生可運用如樣板網表(template netlist)進行字串替換來輕易達成; 對於和幾何相關的案例(後佈線或2D傳輸線或3D結構以場解進行), 則得需要更複雜的程序才能將取樣點轉成測試案例。不論那種程序,最後的結果是每一個測試點表示矩陣裡的一個行而必需要有相對應的案例產出。
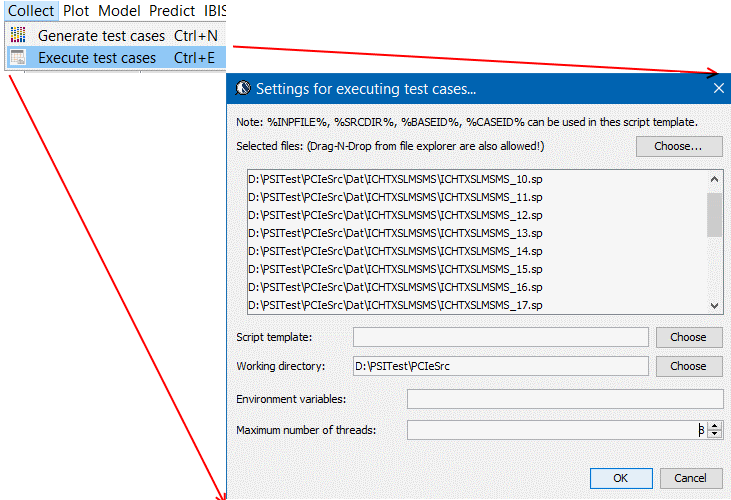
- 對案例仿真、場解並後處理: 再來就是對產出的測試案例仿真、場解及後處理以得到輸出了; 因為可能有維數上千或上萬的案例需進行, 故一般是透過多執行緒或甚至是利用多台電腦來平行處理,最後再將每個案例的算出結果組合以便和原始輸入形成對應關係; 而在這一步驟中所著重的便是如何迅速有效的管理這些平行處理的案例分析。
- 為輸入至輸出建模: 有了輸入及輸出後, 接下來的就是實際的建模了, 若是反應曲面模型, 則可用前述的奇異值分解(SVD)來解相關係數; 其它的建模方式也包括了類神經網路等等;而模型的優劣則可透過其對現有結果的預測及殘值大小來查驗; 殘值(及實際值及預測值間差)愈小則模型愈好; 一般上可用R^2, 即因模型所造成的變異數, 來計模型好壞, R^2 >= 0.95表示是可接受的預測模型。
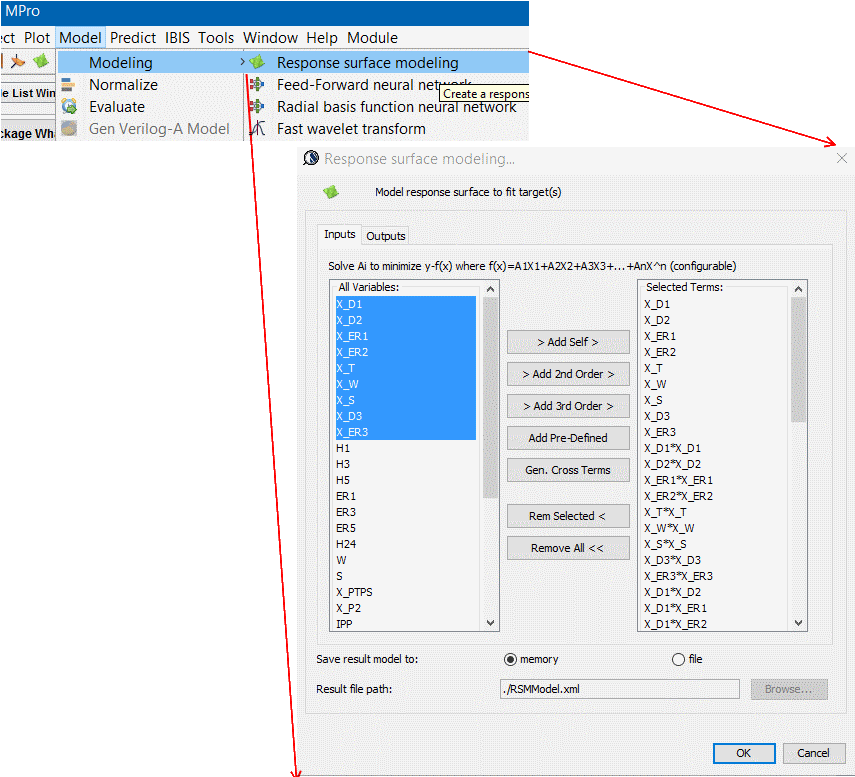
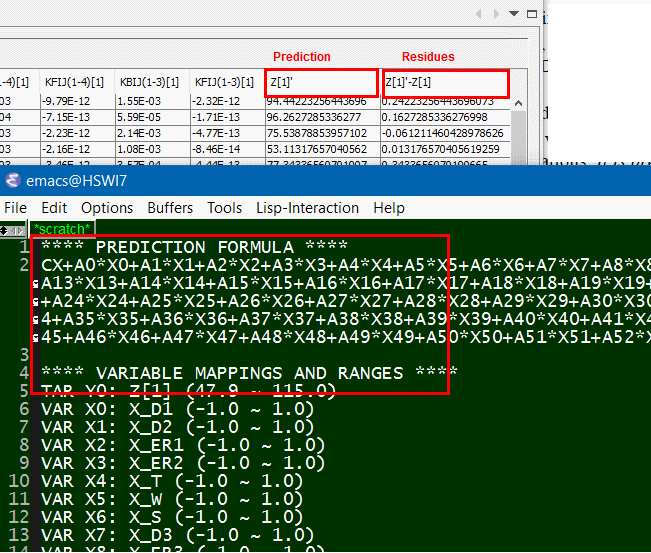
- 優化: 優化是在一定的變量範圍及條件(如不以是負值)等的前題下進行; 而後對單一輸出Y或是以比重組合出的複合Y (or cost function)來求極大極小化; 取決於所取變量的階度, 也有以下幾種演算法可運用:
- 線性規劃: 若變數皆為一階且無cross terms, 則可用線性規化方式得到絕對解; 一般而言, 很多和幾何相關的計算(如layer stackup對阻抗的反應)等都只需要用到一階就可有很好的近似;
- 非線性方法:常有高階項時, 可試著用如Nelder algorithm來求優化值;
- 基因演算法: 這是需經過許多迴圈但可適用於近乎所有模型(含類神經網路)的優化方式。
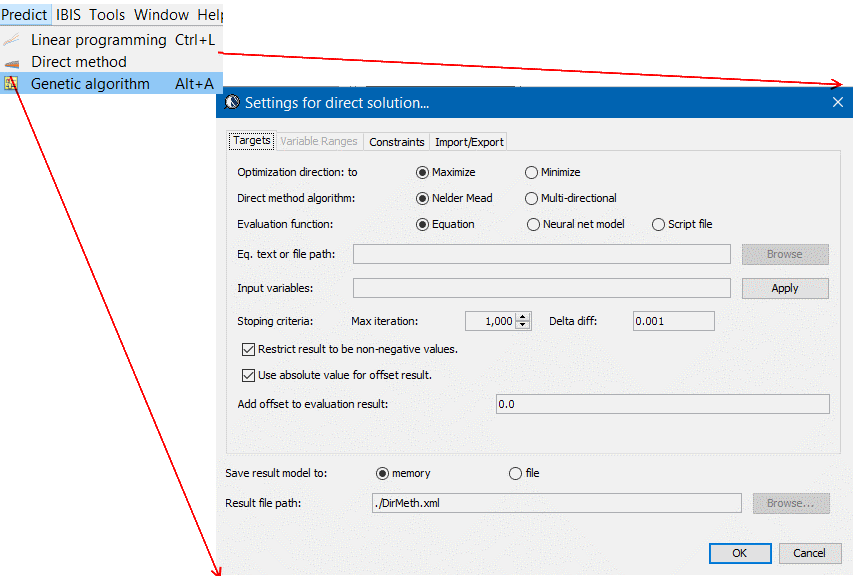
- 審視相關係數及殘值,重覆進行: 最後一步驟則是審視模型中各變量的相關係數, 剔除非主要的變量後再在下一迴圈裡做更進一步的操作; 也可能是對高殘值之案例更進一步檢查看是否是仿值或後處理的過程產生問題以造成離群值。
由上可見, 相較前一則貼文裡所提到的假設性分析, 欲以DOE/RSM的方式來為系統做優化是需要進行更多步驟的及計算資源的; 在另一方面, 一旦所建模型可具預測性(即殘值小), 則此一模型可做為假設性分析的基礎而取代很多不必要的仿真; 下圖中所示:我們的TPro模組先已透過對十數萬案例進行二維場解及建模而能將結果拿來建置成一快速的假設性分析功能使讀者可很快地透過拉BAR來得到相關的性能資訊。